浅谈特征值与特征向量的应用

◎王亚峰 冯文爽 （河北大学，河北 保定 071000）

一、振动理论

振动理论可应用于实际工程的诸多领域，此部分主要对多自由度振动系统的简单求解过程展开讨论，过程中涉及矩阵的特征值与特征向量问题，并简单阐述其实际意义．

无阻尼多自由度系统的自由振动方程如下（n 为自由度）：

矩阵形式为

其中，

它们分别为系统的质量矩阵、刚度矩阵、位移矢量和加速度矢量．

设n 自由度系统运动微分方程①的特解为

将③代入②，化简可得

此式定义了一个n 维广义特征值问题，将其改写为标准特征值问题，即

于是可得系统的特征方程：

则可求出特征值λ 或ω，ω 称为固有频率或自然频率（单位：rad／s），A 为特征向量或模态向量，也称为主振型．

求解特征方程，可求出n 个特征值，将它们按大小顺序排列为λ1≥λ2≥λ3≥…≥λr≥…≥λn-1≥λn，

相应的固有频率为

0≤ω1≤ω2≤ω3≤…≤ωr≤…≤ωn-1≤ωn，

其中，ωr称为系统的第r 阶固有频率，最大特征值λ1对应的最小频率ω1称为第一阶固有频率或基频，这是在工程系统应用中最重要的固有频率．

将ωr代入④或⑤即可得到第r 阶模态向量A（r），即第r阶主振型．

【例1】如图1 所示的质量—弹簧系统，若m1＝m2＝m3＝m，k1＝k2＝k3＝k，求其各阶固有频率和主振型．

解受力分析如图2 所示．

图1

图2

分别建立m1，m2，m3的动力学方程：

质量矩阵和刚度矩阵分别为

动力矩阵为

故特征值问题为

解特征方程可得特征值

注：由于特征向量只取决于各个向量间的比例，与绝对尺寸无关，故以上结果人为地选定

二、主成分分析

在实际应用中，解决某一问题通常涉及很多变量，增加了计算的复杂程度，而且有可能因为个别变量的极端情况而使整体的一般性规律发生偏移．因此，我们希望能够从数据中提取最主要的信息，使用旧变量的线性组合构造新变量，使高维数据投影为低维数据．主成分分析就是一种常用的降维手段，如下面的两个实例（图3，图4）．

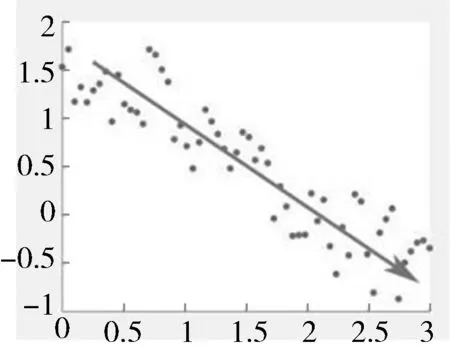
图3 二维降至一维

图4 三维降至二维

下面借助图3 来说明主成分分析的原理．主成分分析指选取一组数的共性的主要部分，忽略次要的不重要部分．图中数据大致沿斜线分布，若将数据投影到斜线上，数据分散度最大，即方差最大，最能体现数据间的主要差异．若用（x11，x21）表示原始数据，则新变量z ＝ax11＋bx21＋c（a，b，c∈R）．这就是降维后的结果，我们要做的就是找到这样一种投影变换，使新变量的方差最大，将z 称为第一主成分．对于更高维的数据，我们可能需要多个主成分，并且主成分之间两两正交．

下面求解这一过程：待研究数据表示为矩阵X∈Rn×d，目标是将d 维数据提取其主成分转为d′维．

其中，n 为样本数，d 为维度，每行为一个样本，每列为一个维度（即一个变量），为第i 个样本．

数据的协方差矩阵如下：

这里假定样本矩阵已经中心化（即每一维度上的均值为0），未中心化时该式不成立．注意：协方差矩阵∑半正定且对称，故∑＝∑T，且∑的特征值都是非负数．

在主成分分析中我们希望数据投影的方差最大，使用线性变换g1，将X 投影到一维空间后，新的数据表示为Xg1，对应方差为

求解g1可得X 投影到Xg1，得X 的第一主成分．

求解第i 主成分时，即求解问题

设协方差矩阵的特征值为λ1≥λ2≥λ3≥…≥λd＞0，这里的g1是∑最大特征值对应的特征向量，g2是∑第二大特征值对应的特征向量，gi是∑第i 大特征值对应的特征向量．这里不做证明．

可见，求解主成分就转化为求解∑的特征向量问题，即投影矩阵G＝（g1，g2，…，gd′），这里要注意的是特征值λi在主成分分析中的实际意义，即某一主成分占总体数据的“比重”． 第i 个主成分的“比重” 为前i 个主成分的“比重” 为

【例2】对于给定的样本，进行主成分分析，降至一维．

解显然待研究数据是4 组二维样本，n ＝4，d ＝2，目标维数d′＝1．

①对样本X 进行中心化，得

②计算协方差矩阵：

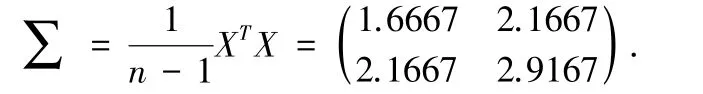
③计算协方差矩阵的特征值和特征向量：

λ1＝4．5467，对应的特征向量为

λ2＝0．0367，对应的特征向量为

④根据要求取前d′个最大的特征值对应的特征向量，

这里d′＝1，并且λ1＞λ2，故我们取G＝g1．

⑤将样本通过投影矩阵G 进行降维，可得结果