基于“怀特海三段论”的概念教学——以不定积分为例

◎邵 云 （滁州城市职业学院，安徽 滁州 239000）

一、怀特海教育节奏

怀特海认为，教学应当遵循浪漫、精确、综合运用三阶段螺旋式上升的节奏．在浪漫阶段，已有知识作为直接认知，学生此时的知识体系是凌乱的，未加整理和梳理．这个阶段是精确阶段的基础，教师应最大限度地调动学生的积极性，把碎片化的知识调出来．精确阶段需要对浪漫阶段凌乱的知识体系进行梳理，对浪漫阶段的一般事实做出揭示和分析，更为重要的是在分析过程中形成思维习惯，提升学习能力．综合运用阶段是在“浪漫”和“精确”之后又重回“浪漫”，它是一个循环的结束，又是另一个循环的开始．

二、高等数学教学现状

“怀特海三段论”在中小学课程教学中得到了广泛的应用，很多教师即便不了解这个理论，在实际的教学中也能遵循浪漫、精确、综合运用的教育节奏，取得良好的教学效果．而在大学课程教学中，此理论鲜少应用．尤其是在着重计算的微积分部分，有关计算方法的研究论文很多，而对相关概念教学的研究几乎是空白，也很少有教师深入细致地剖析概念，这在一定程度上导致学生对基本概念认知模糊，造成了思维的混乱，外部表现就是：无法灵活运用知识解决问题，学到的知识只是一个个碎片，无法形成知识体系．

本文以不定积分的概念教学为例，简要分析如何在教学中灵活运用“怀特海三段论”帮助学生学习知识，形成知识体系．

微积分作为高等数学的重要组成部分，在培养学生的数学思维、提升数学素养方面起着举足轻重的作用，它也是后续课程学习的基础．在实际教学的过程中，教师往往看重计算，花费大量的时间和精力总结和介绍计算方法，对概念只是简单地按照书本讲解，很少进行剖析，更遑论与前、后知识的联系和比较．学生虽然知道如何计算不定积分，但对其中的原理和蕴含的数学思想却知之甚少，甚至连基本的概念都无法论述清楚．这就导致学生在学习微积分时充满困惑，也是很多学生觉得微积分难以理解的根本原因．

通常情况下，我们会把不定积分看作导数（微分）的逆运算，计算定积分的牛顿—莱布尼茨公式也需要借助不定积分，可见不定积分在微积分中占据着极其重要的位置．对不定积分概念的理解有助于加深对导数（微分）的认识，同时为定积分的学习奠定基础．

三、应用“怀特海三段论”的不定积分概念教学

下面先介绍与不定积分相关的两个定义．

定义1设函数F（x）和f（x）都在区间I 内有意义，且对任一x∈I，都有F′（x）＝f（x）或dF（x）＝f（x）dx，则称F（x）是f（x）在I 内的一个原函数．

定义2函数f（x） 在某区间I 内的全体原函数称为f（x） 在区间I 内的不定积分，记作

（一）浪漫阶段

一般情况下，在介绍原函数的定义时，我们会提醒学生注意原函数前面的定语“一个”，而忽视对“F′（x）＝f（x）或dF（x）＝f（x）dx”的深入剖析；在介绍不定积分的概念时，我们只是简单地将几个符号介绍一下，由定义结合基本求导公式给出基本积分公式，而对于概念的深入分析少之又少．概念的模糊不清导致思维的混乱，混乱的思维导致学习定积分时困难重重．在浪漫阶段，需要最大限度地调出与不定积分有关的概念，这些概念可以是混乱模糊的，也可以是精确表述的．为了帮助学生充分了解不定积分的相关信息，我们在这里提出三个问题．

问题1F′（x）＝f（x）与dF（x）＝f（x）dx 有无区别？

两者的联系是学生所熟知的：导数与微分除了形式上有区别，在计算上没有差别．所以这里着重考察两者之间的区别．

问题2不管课程的名称是“高等数学”“经济数学”，还是“数学分析”，该部分内容都叫“微积分”．但是在微分部分，大部分篇幅都在介绍导数，对微分的介绍很少，那么为何不把该部分称为“导数与积分”呢？

问题3探究的异同，以及与的异同．

解答以上三个问题时，需要调出的知识包括基本导数公式、复合函数求导数、微分的计算、链式法则等．

（二） 精确阶段

我们以函数y ＝（3x ＋1）2求导数为例来比较复合函数求导数和链式法则．

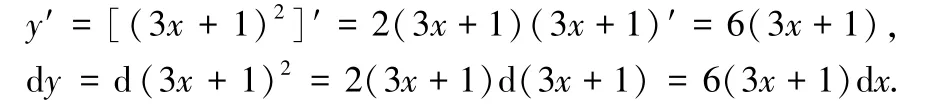
由两个计算过程我们可以清楚地看到，微分的计算更看重整体代换．因此，熟练掌握微分的计算，可以帮助学生加深对基本积分公式的理解．

在计算复杂函数的导数时，使用导数的符号不能清晰明了地表明导数是关于哪个变量进行的．函数不管多么复杂，其表现形式都没有区别，这就使得学生在计算过程中会误认为只能关于x 求导数．这种缺乏整体观的惯性思维导致学生在面对积分变量这个概念时束手无策，从而难以灵活地进行积分的计算．

在实际计算微分时，我们通常采用先计算相应的导数、然后代入微分形式的做法，这对培养学生的整体代换思想是极其有害的．更重要的是，在理解导数公式和积分公式时，不能将整体代换思想灵活运用，会给理解微积分带来负面影响．

下面把基本积分公式改写成类似的形式：

由右侧的公式能够清晰地看到整体，其在应用方面明显优于左侧的公式．学生在识记公式时只有把整体的概念代入其中，学习换元积分法时才会水到渠成．

（三）综合运用阶段

现在，我们可以引导学生将导数基本公式按照上述方法重新进行表述．例如，我们可以将幂函数的导数公式（xα）′＝αxα-1写成（Wα）′＝αWα-1．当然，这种形式不太严谨，更严格的应该是（Wα）W′＝αWα-1，但这种形式很烦琐，所以我们在对复合函数求导数时通常不采用这种形式．为了清晰明了地表达这个过程，我们借助于微分形式dWα＝αWα-1dW，在这个微分表达式中可以清晰地看到此时的导数是关于W 进行的，而W 可以是任何一种表达式．这是微分在表现形式上优于导数的地方，也是我们将有关内容称为“微积分”的一个原因．我们在用语言表述时，可以采用“α 次方求导等于α 倍的（α-1）次方”这样一种表述方法，将W 或者x 都忽略掉，仅仅把运算表述清楚．从本质上说，导数或者积分都是一种运算，运算针对的是函数，函数主要考察的是对应法则也就是映射关系，而与变量的表现形式没有关系．通过对前、后知识的梳理，将导数运算、微分运算、不定积分运算与函数和函数的运算联系起来，学生不仅对不定积分的定义有了深入的了解，也对函数有了更加深刻的认识，从而搭建起了连接初等数学和高等数学的桥梁．

结 语

长期以来，数学教育，尤其是高等数学教育，只注重对学生计算能力的培养，而忽视了对基本概念的教学．基本概念的模糊不清势必造成思维的混乱，从而导致学生对高等数学望而却步．在概念教学中应用怀特海的教育节奏理论，能更加有效地帮助学生将已有的知识进行归纳梳理，形成知识体系，锻炼思维，提升能力．