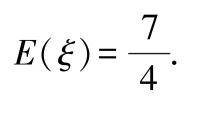2020 年高考数学备考

◎苗金利 （北京四中，北京 100034）

2020 年高考，数学学科把握正确的政治方向，坚持以“立德树人”为核心，树立以人为本的高考价值观，命题方向从关注分数逐渐向关注人的发展过渡；能力内涵不断扩大，强化数学文化因素，数学价值理念增强，强化数学工具、数学应用、数学美，即“万物皆数”；坚持高考制度的改革，坚持稳字当头、稳中有新．

一、试题注重“常规朴素”,考查基础知识

2020 年3 月初，北京市与海南等省进行了高考适应性摸底检测（北京四中采取的是网络发卷、网络阅卷，有的学校用邮政快递投送），无论是主观题还是客观题，都加强了对基础知识的考查，很好地突出了教学重点，注重常规数学思想方法、通性通法的渗透．但基础并不等同于简单、容易，这里的“基础”强化对通性通法的考查，仍需一定的思维品质及运算能力，如下面的劣构问题．此类试题一定有一些“味道”，不可能像“白开水”那样无滋无味．

（2020 年3 月北京市高考适应性测试17 题）已知｛an｝是公比为q 的无穷等比数列，其前n 项和为Sn，满足a3＝12，．是否存在正整数k，使得Sk＞2020？ 若存在，求k 的最小值；若不存在，说明理由．

（注：如果选择多个条件分别解答，按第一个解答计分）

二、试题“稳中有新”,凸显高考改革及新课程改革理念的精髓

数学文化、数学应用来源于生活实际，“编”的痕迹逐渐变淡；数学运算寓于数学主干知识之中，有机结合．2019 年的高考数学试题，让我们感受到高考改革及课程改革浓厚的气息，新课程的理念和评价思路渗透在试题中，考查目标更是与新课程的教学要求有比较紧密的相关性，能够让人明显感觉到高考与课标要求之间的对接与配合，试题体现出稳定之中有新意、有亮点、有变化的共同特点，如2019 年高考数学全国Ⅰ卷中的第四题，求“断臂维纳斯”的身高．

三、考查数学本质,是学生所接受数学教育的展示舞台

高考数学将传统常规与时尚创新巧妙结合，注重“时尚”及“传统”的结合，变化试题结构和形式，考查数学“本源”及对数学“整体”的理解与把握，拒绝八股文似的“套模”，更有利于全体考生正常发挥，“让试卷成为考生展示自己风采的舞台”，“尊重考生12 年的付出”，“考查考生的创新精神和潜质，增强试题的科学性、公平性和规范性”．高考数学在进一步处理好“知识与能力”考查的同时，适当加大“过程与方法”的考查力度，兼顾“情感态度与价值观”的考查．例如，2019 年高考数学全国Ⅰ卷中，概率统计题放在选做题之前作为最后一道压轴题；北京市2020 年高考适应性测试中，立体几何题为第一道大题，调整了试题位置．

四、高考改革与学科趋势分析,暨2020 年高考备考指导

2020 年，全国大部分省市高考制度改革，近几年新课程标准、新教材均处于过渡期，“和谐”稳定的高考命题成为广大考生、家长及全社会的共同期待．

关于2020 年高考数学备考，总的建议如下：

（1）立足基础落实，理解概念本质，整体把握试题；

（2）突破模式化，培养数学思维能力，以不变应万变；

（3）数学文化（如世界与中国，物理，化学，天文，经济），数学应用（如劳动美，数学美——星形线、两个半椭圆、三朵云、维纳斯），数学建模；

（4）在题型结构控制难度的基础上，小题多空，开放小题、劣构试题、多选题等，提高对思维品质的考查；

（5）有效备考要注意：按部就班不跳步，有规律地去刷题，学会系统和自检．

具体来说，高考数学备考要以知识为主线（区别于方法），包括从知识内容到对数学的整体把握、从解题方法策略到考试答卷时的得分感觉．

下面是笔者在中国教育电视台2020 年“同上一堂课”期间整理的部分试题，供同学们复习时参考．

例1在△ABC 中，AC＝BC，P1，P2，P3为AB 上的点，且则（ ）．

A．I1＜I2＜I3B．I1＜I3＜I2

C．I3＜I2＜I1D．I2＜I1＜I3

答案:D

例2已知直线x＋y＋2 ＝0 与圆x2＋y2＋2x-2y＋a ＝0 无公共点，则实数a 的取值范围为．

答案:（0，2）

例3用不等臂天平称质量为4 g 的药品，先放在左盘上称，再放在右盘上称，记下两次的结果．其记录数据可能是下列的哪一组？ （ ）．

A．2 g，6 g B．4 g，1 g

C．10 g，6 g D．2 g，8 g

答案:D

例4某学校数学建模小组为了研究双层玻璃窗中每层玻璃的厚度d（每层玻璃的厚度相同）及两层玻璃间所夹空气层的厚度l 对保温效果的影响，利用热传导定律得到热传导量q 满足关系式：q ＝λ1·其中，玻璃的热传导系数λ1＝4×10-3焦耳／（厘米·秒·摄氏度），不流通、干燥空气的热传导系数λ2＝2．5×10-4焦耳／（厘米·秒·摄氏度），ΔT 为室内外的温度差．q 值越小，保温效果越好．现有四种型号的双层玻璃窗，具体数据如下表：

答案:B

例5已知a，b，a＋m 均为大于0 的实数，给出下列五个论断：

以其中的两个论断作为条件，从余下的论断中选择一个作为结论，请你写出一个正确的命题：．

答案:①③⇒⑤（答案不唯一）

例6某地一种出租车的车费的计算规定如下：

①基本车费为7 元，行程不足或等于3 公里时，只收取基本车费；

②行程不足或等于5 公里时，大于3 公里的那部分，每增加0．5 公里加收车费0．7 元，不足0．5 公里按0．5 公里计算；

③行程大于5 公里时，大于5 公里的那部分，每增加0．2公里加收车费0．4 元，不足0．2 公里按0．2 公里计算．

如果某人从A 地到B 地的行程为4．3 公里，那么车费为元；如果某人从A 地到B 地共付车费11 元，那么行程x 公里的取值范围是．

答案:9．1；（5．4，5．6］

例7在平面直角坐标系中，曲线C 是由到两个定点A（1，0）和B（-1，0）的距离之积等于的所有点组成的．对于曲线C，有下列四个结论：

①曲线C 是轴对称图形；

②曲线C 是中心对称图形；

③曲线C 上所有的点都在单位圆x2＋y2＝1 内；

答案:①②

例8一个国际象棋棋盘（由8×8 个方格组成），其中有一个小方格因破损而被剪去（破损位置不确定）．“L”形骨牌由三个相邻的小方格组成，如下图所示．现要将这个破损的棋盘剪成数个“L”形骨牌，则（ ）．

A．至多能剪成19 块“L”形骨牌

B．至多能剪成20 块“L”形骨牌

C．一定能剪成21 块“L”形骨牌

D．前三个答案都不对

答案:C

例9已知△ABC满足下列四个条件中的三个：

（Ⅰ）请指出这三个条件，并说明理由；

（Ⅱ）求△ABC 的面积．

答案:（Ⅰ）①③④；（Ⅱ）6 3．

例10某地区高考实行新方案，规定：语文、数学和英语是考生的必考科目，考生还须从物理、化学、生物、历史、地理和政治六个科目中选取三个科目作为选考科目．若一名学生从六个科目中选出了三个科目作为选考科目，则称该学生的选考方案确定；否则，称该学生的选考方案待确定．例如，学生甲选择了物理、化学和生物三个选考科目，则学生甲的选考方案确定，“物理、化学和生物”为其选考方案．某学校为了解高一年级420 名学生选考科目的意向，随机选取30 名学生进行了一次调查，统计选考科目人数如下表：

性别 选考方案确定情况 物理 化学 生物 历史 地理政治选考方案确定的有8 人 8 8 4 2 1 1男生选考方案待确定的有6 人 4 3 0 1 0 0选考方案确定的有10 人 8 9 6 3 3 1女生选考方案待确定的有6 人 5 4 1 0 0 1

（Ⅰ）估计该学校高一年级选考方案确定的学生中选考生物的学生有多少名．

（Ⅱ）假设男生、女生选择选考科目是相互独立的．从选考方案确定的8 名男生中随机选出1 名，从选考方案确定的10 名女生中随机选出1 名，试求该男生和该女生的选考方案中都含有历史科目的概率．

（Ⅲ）从选考方案确定的8 名男生中随机选出2 名，设随机变量求ξ 的分布列及数学期望E（ξ）．

答案:（Ⅰ）140 名．（Ⅱ）

（Ⅲ）ξ 的分布列为