源于标准,基于考纲,回归本质,关注素养——例析二次函数为背景的中考选择题命题

新疆乌鲁木齐市教育研究中心

随着教育部《关于全面深化课程改革落实立德树人根本任务的意见》的颁布与实施,聚焦学生数学核心素养成为近年中考数学命题的落脚点.二次函数作为初中数学学习的重点内容之一,也是初中数学与高中数学联系的纽带,关于二次函数的相关试题能够比较广泛地考查到学生函数与方程,数形结合,分类讨论及转化等思想方法,无论是在知识、思维和综合方面都一直处在中考中的重要位置,所以近年来以二次函数为背景的中考题层出不穷,下面以几道中考题为例,分析以二次函数为背景的选择题的命题方向及解题思路.

1 对比课标要求分析中考试题的命题误区

近年来对二次函数为背景的中考试题在命题方向上还是存在着一些误区,这些试题并没有从根本上明确课程标准对函数的要求,盲目追求人为设定的解题技巧即所谓“综合能力”,其实往往偏离了对概念本质的导向,也会影响一线教师在日常教学中对学生数学核心素养的培养.

我们首先来看一下《义务教育课程标准(2011版)》(下文简称课标)中对“函数”及“二次函数”内容的要求:

函数:

(1)探索简单实例中的数量关系和变化规律,了解常量、变量的意义.(2)结合实例,了解函数的概念和三种表示法,能举出函数的实例.(3)能结合图像对简单实际问题中的函数关系进行分析.(4)能确定简单实际问题中函数自变量的取值范围,并会求出函数值.(5)能用适当的函数表示法刻画简单实际问题中变量之间的关系.(6)结合对函数关系的分析,能对变量的变化情况进行初步讨论.

二次函数:

(1)通过对实际问题的分析,体会二次函数的意义.(2)会用描点法画出二次函数的图像,通过图像了解二次函数的性质.(3)会用配方法将数字系数的二次函数的表达式化为y=a(x-h)2+k的形式,并能由此得到二次函数图像的顶点坐标,说出图像的开口方向,画出图像的对称轴,并能解决简单实际问题.(4)会利用二次函数的图像求一元二次方程的近似解.(5)知道给定不共线三点的坐标可以确定一个二次函数.

下面我们比对课标来看一看以下几道中考题的命题方向.

例1【2018·兰州中考数学题】已知二次函数y=ax2+bx+c(a0)的图象如图1所示,有下列5个结论:abc＞0;b-a＞c;4a+2b+c＞0;3a＞-c;a+b＞m(am+b)(m1的实数).其中正确结论的有( )

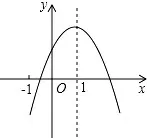
图1

图2

例2 【2018·湖南衡阳中考数学题】如图2,抛物线y=ax2+bx+c与x轴交于点A(-1,0),顶点坐标(1,n),与y轴的交点在(0,2),(0,3)之间(包含端点),则下列结论:3a+b＜0;-1≤a≤-;对于任意实数m,a+b≥am2+bm总成立;关于x的方程ax2+bx+c=n-1 有两个不相等的实数根.其中结论正确的个数为( )

A.1个 B.2个 C.3个 D.4个

图3

图4

例3【2015·乌鲁木齐中考数学题】如图3,抛物线y=ax2+bx+c的对称轴是x=-1,且过点有下列结论:abc＞0;a-2b+4c=0;25a-10b+4c=0;3b+2c＞0;a-b≥m(am-b),其中所有正确的结论是____.(填写正确结论序号)

例4【2017·山东烟台中考数学题】二次函数y=ax2+bx+c(a0)的图象如图4所示,对称轴是直线x=1,下列结论:ab＜0;b2＞4ac;+b+2c＜0;3a+c＜0.其中正确的是( )

例举的这四道中考题是近年来非常流行的考查方式,但这种考查方式过度“解析化”,过度强调所谓的“数形结合”,学生并未从函数建模的本质出发,均是直接给定函数图象与对称轴或者交点坐标,让学生判断含有二次函数解析式系数的式子的范围或取值.表面上考查了二次函数的解析式系数与图象的关系,函数与方程,函数与不等式等相关知识,但实则单纯一味拼凑了一系列“套路”,掐头去尾的设定,学生则为了解题而解题,对二次函数的来源和应用关注不足,这种命题方向并未体现课标中对“变量与函数”部分的本质导向.

从课标可以看出,二次函数的学习还是要源于生活,最终落实在能解决简单的实际问题,所以,基于课标的二次函数命题应更重视函数的应用意识和综合能力的考查.

2 回归概念本质看二次函数解题思路

由于中考试题的导向性,一线教师也有针对性的对此类二次函数的试题总结出了一整套的“套路”,比如:“一看开口决定a,左同右异确定b,c看y轴的交点”等等,但这种方法往往是剥离了基础概念,讲解题而不讲怎样解题,不讲如何想到这种解法,一味给学生灌输某种已经归纳概括后的揭发技巧,选取例题时也会往“偏、奇、巧”等方向偏移,不但没有培养学生的能力,还会禁锢学生的思维,应慢慢回归本质,在解题思路方面要从函数解决问题的本质出发,提高学生分析问题、解决问题的能力.

比如上题也可以从二次函数的概念本质出发,将各种含二次函数解析式系数的式子回归到对二次函数解析式的系数的分析上,只要能得到二次函数解析式,明确了系数之后,题目也自然豁然开朗了.

例1 解设此抛物线与x轴的负半轴的交点坐标为(t,0),则另一交点为(2-t,0),易知-1＜t＜0,设抛物线解析式为y=a(x-t)(x-2+t)

=ax2-2ax+t(2-t)a(a＜0)

∴a=a,b=-2a,c=t(2-t)a,

∵-1＜t＜0,

∴2-t＞0,

又∵a＜0,

∴abc＜0,故错误;

∵a＜0,-1＜t＜0,

∴b-a-c＞0 故正确;

∵a＜0,m1,

∴-a(m-1)2＞0,故正确;故正确的为.

例2 解∵顶点坐标为(1,n),与x轴一个交点为A(-1,0),则另一个交点为(3,0)

∴抛物线解析式为y=a(x+1)(x-3),即y=ax2-2ax-3a.

∴a=a,b=-2a,c=-3a.

∴2≤-3a≤3,-1≤a正确;

∵Δ=-4a＞0,正确.

例3 解∵对称轴是x=1,与x轴交于点由对称性易知另一个交点为

∴抛物线解析式为y=a即y=

∴a=a,b=2a,c=且a＜0.于是abc=a·2a·正确;

例4 解设抛物线与x轴负半轴的交点坐标为(n,0)(易知-1＜n＜0)

∵对称轴是x=1,

∴与x轴正半轴交点的坐标为(2-n,0)则此抛物线解析式为y=a(x-n)(x-2+n),即y=ax2-2axan(n-2),

∴a=a,b=-2a,c=-an(n-2)

∵-1＜n＜0,

又∵a(＞0,

∴-2a

∴a+b+2c＜0,故正确;

第二种方法:2n2-4n+1=2(n-1)2-1,

∵-1＜n＜0,

∴1＜(n-1)2＜4,

∴1＜2(n-1)2-1＜7,

即当-1＜n＜0时,2n2-4n+1＞0,

∴-a(2n2-4n+1)＜0,故正确;

∵a＞0,-1＜n＜0,

∴n-3＜0,n+1＞0,

∴3a+c＞0,故错误.

初中阶段的函数概念是动态的,重点在于运动变化的过程中变量之间的关系,在遇到实际问题时,需要学生主动发现运动变化中的变量关系,在关系发现的过程中潜移默化的渗透数学抽象,模型思想,即便这几题均没有实际问题的背景,但在教学过程中也要把问题回归到函数概念生成的原点,关注二次函数概念的本质.上面解题使用的方法,抛离了总结的所谓“套路”,虽然看似解法变复杂了,但实则回归了二次函数概念的本质,把此类问题划归为对二次函数解析式的确定,明确二次函数解析式中的待定系数,用更严谨的思维和更规范的表达,体会解决二次函数问题的一般方法.