一种常规机动下机载SINS/GPS 组合导航系统的可观测性分析

夏宇强，张 林，陈善秋

（北京航天时代激光导航技术有限责任公司， 北京 100094）

0 引言

目前，捷联惯性/卫星（SINS/GPS）组合导航系统是机载领域最为常见的组合导航系统［1］。为保证惯组的导航精度能够达到要求，需要对其定期进行返厂标定，成本高、周期长，也影响载机的使用效率，故而机载惯组在线标校技术的研究一直在不断进行中。在线标校的精度很大程度上取决于滤波器对各状态量的估计速度和估计精度，故而需要对系统的可观测性进行分析。而系统的可观测性又与载机的机动状态密切相关，复杂的机动有利于提高系统的可观测性。但对于像运输机等体积较大、机动能力较差的机型，其很难进行复杂的机动动作，所以需要对其静止、起降、匀速飞行、匀加减速飞行、转弯等一系列常规机动动作进行分析，用以探究如何有效利用这些过程来提高机载SINS/GPS组合导航系统的精度，达到满足机载惯组在线标校的要求。

目前，国内主要采用计算可观测性矩阵的秩的方法来分析时不变（LTI）系统的可观测性；而对于时变系统，直接进行可观测性分析需要计算Grammian矩阵，计算复杂且无法进行理论分析。以色列学者Goshen-Meskin等［2］提出了一种分段线性定常系统（PWCS）可观测性分析方法，但该方法只能定性判断系统是否完全可观测，无法准确判断具体的某一状态量是否可观测，更无法定量分析具体的某一状态量的可观测度。东南大学的程向红等［3］提出了奇异值分解（SVD）方法，通过对可观测性矩阵的奇异值进行分解，实现了对系统状态量可观测性的定量判断，在工程上得到了广泛的应用［4-6］。

本文采用基于分段线性定常系统的奇异值分解法，对组合导航系统动态过程中滤波器的收敛速度和收敛精度进行量化分析。通过对基于速度位置的SINS/GPS组合导航系统的各种机动状态下的可观测性进行分析研究，得到了一些通过载体机动来提高各状态量可观测度的结论。最后通过Matlab仿真和转台实验，证明了这些结论具有一定的实用价值，能够为机载惯组在线标校技术的工程化应用提供一定的依据。

1 机载SINS/GPS组合导航系统滤波模型

利用GPS提供的速度信息、位置信息与惯导解算的速度、位置作差，得到速度误差和位置误差作为观测量来设计Kalman滤波器。SINS/GPS组合导航系统的原理框图如图1所示［1，7］。

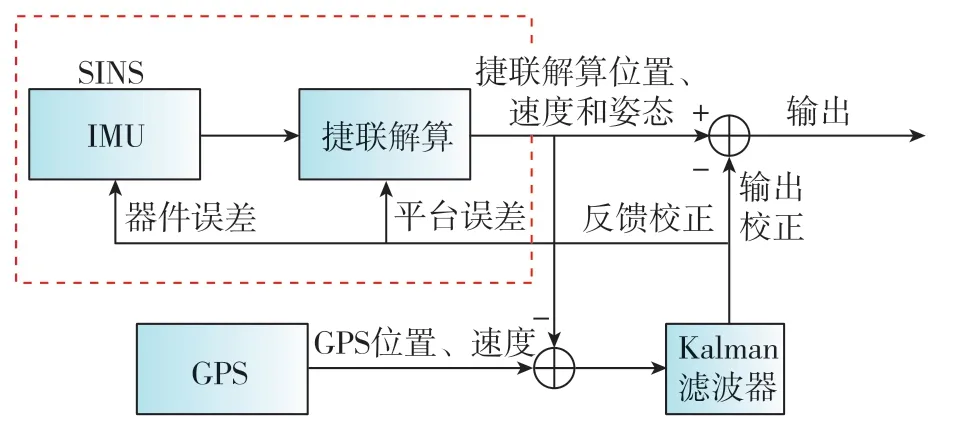
图1 SINS/GPS组合导航系统原理框图Fig.1 Principle block diagram of SINS/GPS integrated navigation system

1.1 系统状态方程

对机载SINS/GPS组合导航系统，选取东北天（E-N-U）坐标系为导航坐标系，状态量的选取如下

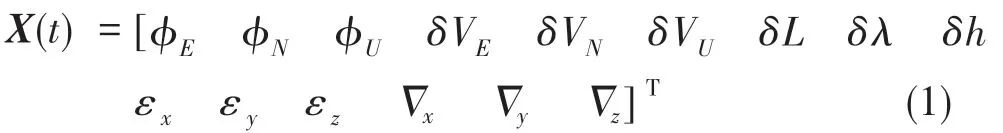
式（1）中，φE、φN、φU为平台误差角，δVE、δVN、δVU为速度误差，δL、δλ、δh分别为纬度误差、经度误差和高度误差，εx、εy、εz为陀螺随机漂移，为加速度计随机偏置。

则系统状态方程表达式为

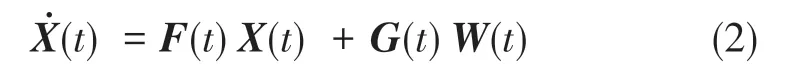
式（2）中，X（t）∈R15为状态变量，F（t）∈R15×15为系统误差矩阵。根据误差模型可知，W（t）∈R6为系统噪声向量，G（t）∈R15×6为系统噪声驱动矩阵。

F（t）、G（t）、W（t）的表达式分别为

式（3）中，FN为对应于SINS的9个误差参数（3个姿态误差、3个速度误差、3个位置误差）的系统动态矩阵，它是9×9阶的方阵。另外，FS和FM分别如下

1.2 系统量测方程

在SINS/GPS组合导航系统中，选择位置、速度组合，则系统的量测值包括两种［1］：一种为位置量测差值，另一种为速度量测差值，故有系统量测方程

式（7）中，Z（t）为系统的量测向量，H（t）为量测矩阵，V（t）为量测噪声向量，其中

2 系统可观测性分析

2.1 基于PXCS的可观测性分析

根据式（2）和式（7）构造SINS/GPS组合导航系统方程，描述如下

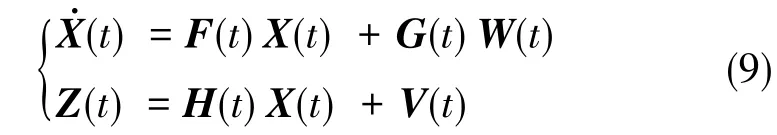
按照能观测性的判定依据，需要计算Grammian矩阵

式（10）中，Φ（τ，t0）为该系统从τ到t0的状态转移矩阵。

若Grammian矩阵为非奇异，那么该系统从τ到t0时间段内完全可观测。但由于F（t）、H（t）均随时间而变化，所以Grammian矩阵只能依赖数值计算方法，计算复杂且无法对结果进行理论分析［8］。

为解决上述问题，Goshen-Meskin等提出了一种分段线性定常系统（PXCS）方法，该分析方法假定F（t）、H（t）在每个时间区间tj（j＝1，2，3，…）内不变，则原系统在每个时间区间内可以等效为线性定常系统［9］，故式（9）可描述为

在每一个时间区间内，对观测矢量Zj（t）进行n-1次微分，有

式（12）可以改写成矩阵的形式

定义Δj（j＝1，2，3，…，r-1）为tj到tj+1的时间间隔，故有

定理1：如果null（j）⊂null（Fj），1≤j≤r，那么，null{（r）}⊂null{s（r）}，rank{（r）}＝rank{s（r）}。

在满足定理1的条件下，可以将PXCS中的TOM用SOM替换掉，进而可以极大简化系统可观测性分析过程。

2.2 基于SVD的可观测度分析

这里简要介绍一下SVD的意义：考虑任意一个矩阵M⊂Rm×n，且rank（M）＝r，则矩阵M一定可以分解为

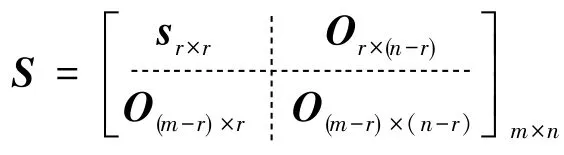
对下面的离散线性系统进行可观测度的分析说明。

式（18）中，X（k）∈Rn，F（k）∈Rn×n，Y（k）∈Rm，H∈Rm×m。

依据式（18），可以推得

式（22）中，Rk为式（18）的可观测性矩阵，系统状态量X（0）估计的好坏取决于Rk矩阵的特性。

对Rk进行奇异值分解

式（25）中，αj为任意数。

显而易见，当r＝min（m，n）时，X（0）有唯一解；当r＜min（m，n）时，X（0）有无数解。此时，X（0）不能通过观测量Y来进行准确估计，即式（18）是否完全可观测取决于Σ中非零奇异值的个数。

当外部观测值Y具有常值范数时，初始状态X（0）形成一个椭球，其方程为

从式（26）和式（27）可以看出，椭球的体积与奇异值的大小成反比，即σi越大，该椭球的体积越小，的可行域就越小，对应的X（0）的估计就越精确；反之，当σi很小甚至为零时，将变得很大，估计是无界的，也就是说X（0）不能由观测量Y估计出来。因此，对可观测性矩阵Rk进行奇异值分解可以用于定量分析系统可观测度的大小，奇异值越大，系统状态的估计精度越高，系统可观测度越高。

3 系统不同机动条件下的可观测性分析

针对飞机静止、起降、匀速飞行、匀加减速飞行、转弯等一系列机动过程，利用上述基于PWCS的SVD分解方法对SINS/GPS组合导航系统进行可观测度分析，具体的分析过程如下：

1）静止状态：此时，系统为时不变系统，可观测矩阵可以直接获取。

2）起降过程：假设飞机以190m/s 的速度准备起飞，分三段。第一段机头匀速拉起到30°，准备爬升；第二段爬升结束，准备改平；第三段机头改平，起飞结束（降落过程与起飞过程相反）。

3）匀速飞行：假设飞机以190m/s 的速度匀速飞行。

4）匀变速飞行：假设飞机在190m/s 的速度时以 2.5m/s2的加速度将飞机加速至250m/s（减速过程与加速过程相反）。

5）匀速转弯：假设飞机以190m/s 的速度匀速左转弯，分三段。第一段机翼左倾斜30°，准备转弯；第二段飞机左转90°，准备改平；第三段机翼右倾30°，转弯结束（右转弯与左转弯过程相反）。

通过对上述机动过程的分析，得到系统各状态分量对应的奇异值分析结果，如表1所示。

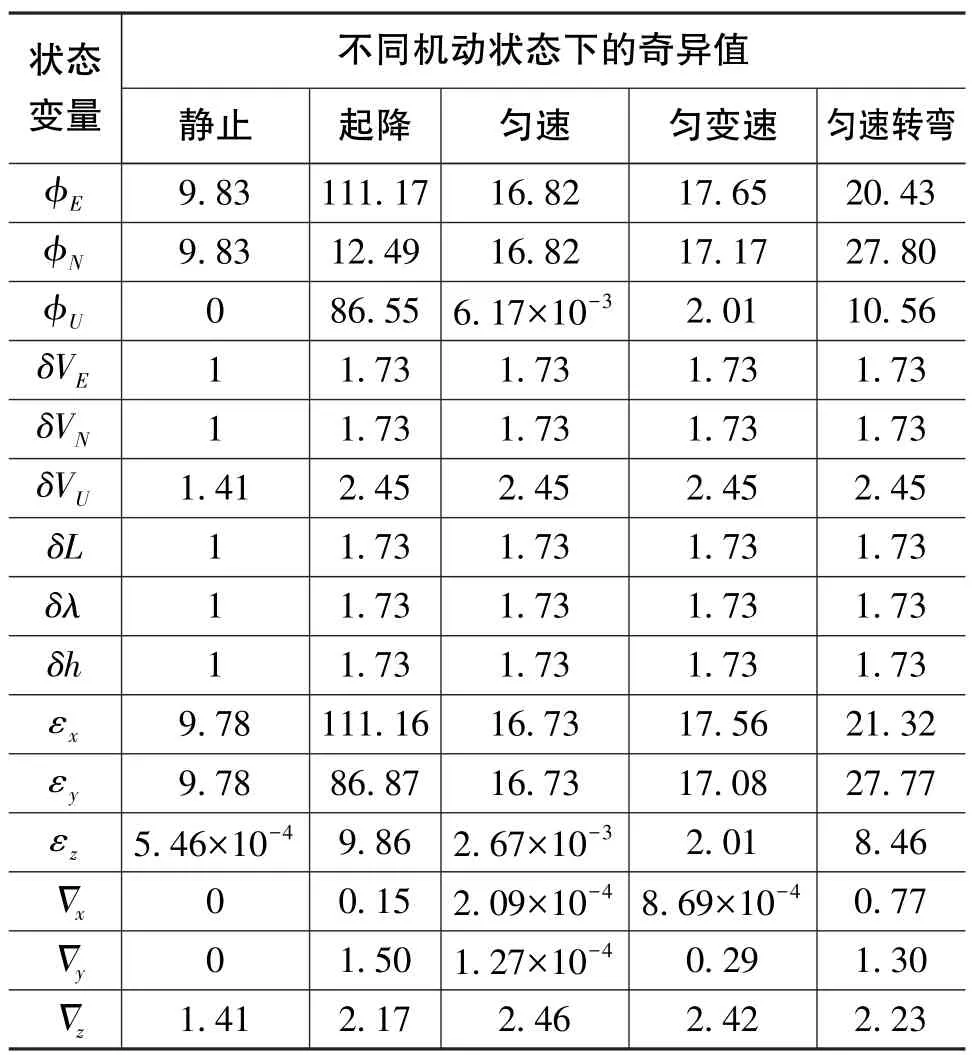
表1 各状态量对应的奇异值分析结果Table 1 Singular value analysis results of corresponding state variables

由于系统采用的是速度、位置的组合，故速度和位置状态量在各种机动状态下均是可观测状态，再通过分析表1中系统可观测矩阵的奇异值，可得如下结论：

1）系统在静止状态下，两个水平加速度计的零偏和方位误差角三个状态不可观测，且天向陀螺漂移的可观测性较差；

2）飞机做匀速直线运动时，系统的可观测度仍较差，两个水平加速度计的零偏、方位误差角和天向陀螺漂移的可观测度仍然较低；

3）飞机做匀加速、匀减速直线运动时，对方位误差角和天向陀螺漂移的可观测度提高较为明显，两个水平加速度计的零偏可观测度仍然较低；

4）在各种机动状态下，东向、北向两个陀螺零偏和天向的加速度计零偏都是可观测状态，从滤波开始即持续收敛，同时增加机动都能使其可观测度得到提高，加快滤波收敛速度；

5）飞机的起降和转弯对系统各状态量的可观测度都有较大提高，尤其是对两个水平加速度计的零偏和方位误差角的可观测度，系统完全可观测。

4 Matlab仿真分析及转台实验

4.1 Matlab仿真分析

Kalman滤波器估计效果的好坏主要通过滤波器的均方误差阵Pk来表征，Pk对角线上各元素的平方根就是各状态估值的误差均方差，从统计意义上其数值是判断各状态估值精度的直接依据。所以，可以通过分析各状态估计误差的均方差，根据其收敛的速度与精度进而判断系统的可观测性。下面通过系统仿真来获取Pk，并通过Matlab仿真结果来直接判断系统的可观测性。

在进行系统的仿真分析时，仿真参数的设置如下：

陀螺的常值零偏为0.1（°）/h，随机漂移为0.05（°）/h，同时选取加速度计常值零偏为100μg，随机偏置为50μg；误差状态初值取为φE＝φN＝150″、φU＝300″、δVE＝δVN＝δVU＝0.1m/s、δL＝δλ＝20m、δh＝50m，滤波周期为1s；GPS速度测量误差噪声为0.01m/s，GPS位置测量误差噪声为5m。

由于系统采用的是速度、位置的组合，故速度和位置状态量具有外部观测信息，在各种机动状态下均是可观测状态，故下面只分析除速度、位置状态量外的其他九个状态量的可观测性。图2～图4为静止状态下平台误差角、加速度计零偏以及陀螺漂移的估计误差标准差曲线，图中的红色实线、绿色虚线、蓝色点划线分别对应东北天三个方向上的状态量。

图2 静止状态下的平台误差角估计误差标准差曲线Fig.2 Error standard deviation curves of platform error angle estimation under static state

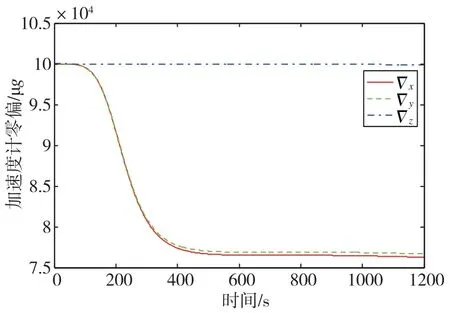
图3 静止状态下的加速度计零偏估计误差标准差曲线Fig.3 Error standard deviation curves of accelerometer zero-bias estimation under static state

图4 静止状态下的陀螺漂移估计误差标准差曲线Fig.4 Error standard deviation curves of gyroscope drift estimation under static state

分析图2～图4所示的系统估计误差标准差曲线，可知系统在静止状态下的两个水平加速度计零偏和方位误差角三个状态不可观测。另外，天向陀螺漂移的可观测性较差。

图5～图7为飞机机动状态下系统各状态量的估计误差标准差曲线，具体机动情况如表2所示。

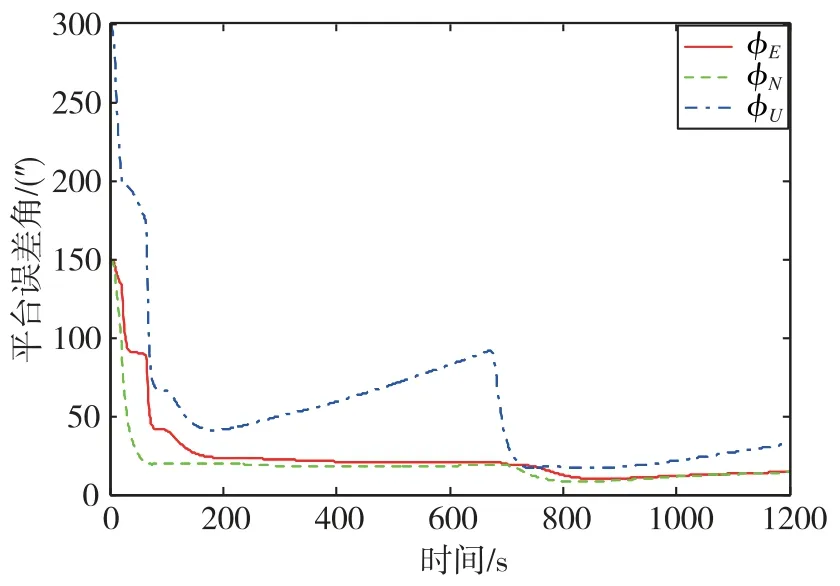
图5 机动状态下的平台误差角估计误差标准差曲线Fig.5 Error standard deviation curves of platform error angle estimation under maneuvering state

图6 机动状态下的加速度计零偏估计误差标准差曲线Fig.6 Error standard deviation curves of accelerometer zero-bias estimation under maneuvering state

图7 机动状态下的陀螺漂移估计误差标准差曲线Fig.7 Error standard deviation curves of gyroscope drift estimation under maneuvering state

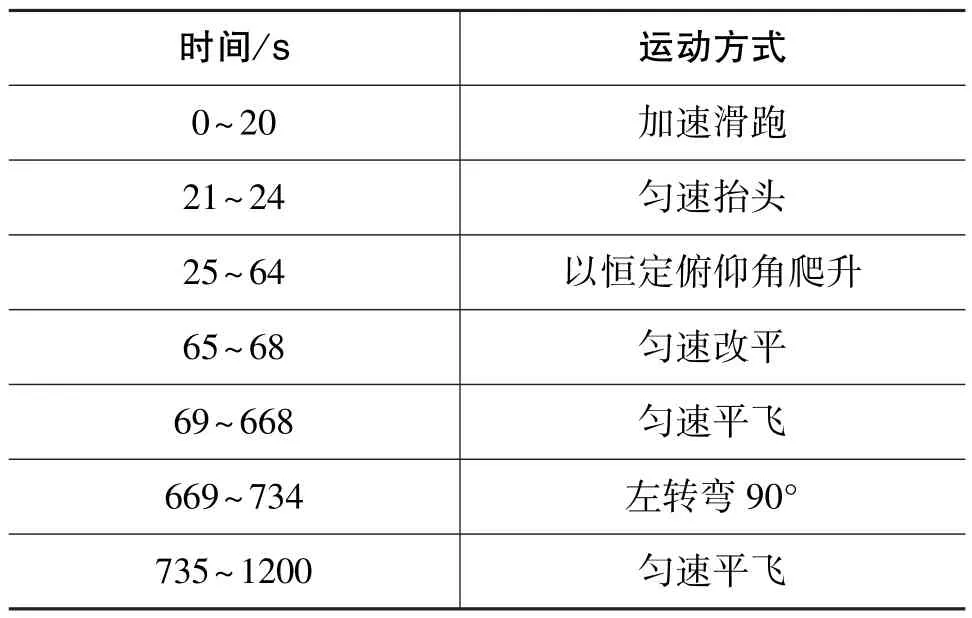
表2 飞机的机动状态Table 2 Maneuverability of an aircraft

分析图5～图7所示的系统估计误差标准差曲线，可以得到：

1）飞机的加速滑跑对东向加速度计零偏可观测度的提高不是很明显，对其他各状态量的可观测度都有较大提高；

2）飞机的起飞过程对系统各状态量的可观测度都有较大提高，尤其是对两个水平加速度计零偏和方位误差角的可观测度；

3）飞机做匀速直线运动时，系统可观测度的提高不是很明显；

4）飞机转弯时，能在起飞过程的基础上再次大幅度提高方位误差角和天向陀螺漂移的可观测度；

5）在各种机动状态下，东向、北向两个陀螺零偏和天向加速度计零偏都是可观测状态，从滤波开始即持续收敛，同时增加机动都能使其可观测度得到提高，加快滤波收敛速度。

4.2 转台实验

将实验惯组放置于三轴转台上，通过转台的静止和旋转来简单模仿飞机的静止、滚动和转弯过程。利用导航软件输出的滤波器对陀螺和加速度计进行零偏估计，与4.1节的Matlab仿真结果进行对比，来进一步验证本文关于采用基于分段线性定常系统的奇异值分解法对系统可观测性分析方法的准确性和实用性。这里未使用实际的GPS信号，位置和速度信息直接是在导航软件中输入转台的固定位置，速度置零。

转台实验分两部分，具体过程如下：

（1）未人为添加误差前

惯组在转台上的初始状态为航向角、俯仰角、横滚角均为0°，首先完成静态初始对准，然后进行20min静态导航，接着航向由0°转到90°，同时横滚角由0°转到60°，航向角和横滚角的转动在1min内同时进行，转动完成后，再进行30min静态导航，得到如图8和图9所示的未添加误差前两个水平加速度计和三个陀螺零偏估值曲线。

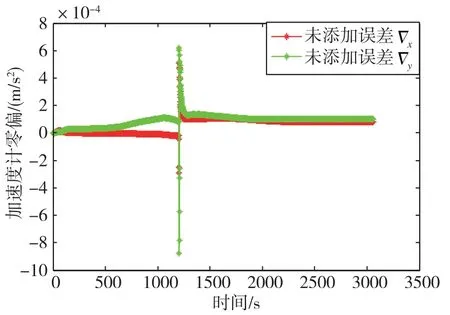
图8 未添加误差之前两个水平加速度计的零偏估值曲线Fig.8 Zero-bias estimation curves of two horizontal accelerometers before adding errors

图9 未添加误差之前三个陀螺的零偏估值曲线Fig.9 Zero-bias estimation curves of three gyroscopes before adding errors

（2）对陀螺和加速度计分别人为添加0.02（°）/h和0.001m/s2零偏误差

重复上述操作，得到如图10和图11所示的添加误差后两个水平加速度计和三个陀螺零偏估值曲线。

对添加误差前后陀螺和加速度计的误差估值作差，得到如图12和图13所示的滤波器对陀螺和加速度计零偏估计效果曲线。

图10 添加误差之后两个水平加速度计的零偏估值曲线Fig.10 Zero-bias estimation curves of two horizontal accelerometers after adding errors

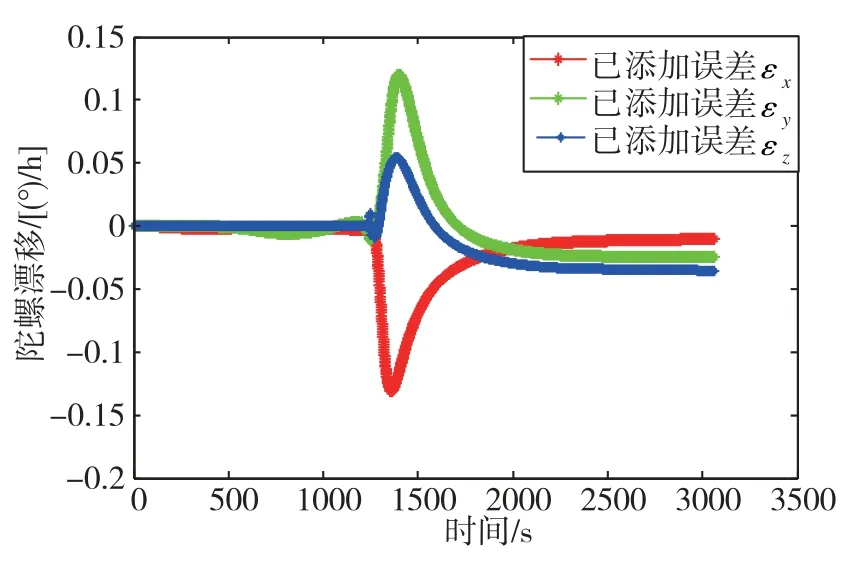
图11 添加误差之后三个陀螺的零偏估值曲线Fig.11 Zero-bias estimation curves of three gyroscopes after adding errors

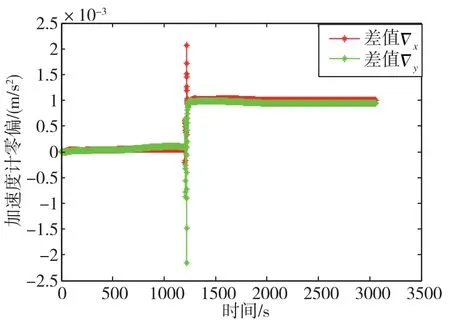
图12 Kalman 滤波器对两个水平加速度计零偏估计的效果曲线Fig.12 Effect curves of Kalman filter on two horizontal accelerometers zero-bias estimation

图13 Kalman 滤波器对三个陀螺零偏估计的效果曲线Fig.13 Effect curves of Kalman filter on three gyroscopes zero-bias estimation

通过分析图8～图13的转台实验结果，可以得到如下结论：

1）通过观察图8可知，静态下两个水平加速度计是完全不可观测的。经过模拟转弯过程后，两个水平加速度计完全可观测。且结合图12可以看出，滤波器对两个水平加速度计添加的0.001m/s2零偏误差估计效果显著，即其可观测度得到显著提高。

2）通过观察图9可知，静态下东向和北向陀螺是可观测的，而天向陀螺则不能被滤波器估计出，即其可观测度较小或者不可观测。而经过模拟转弯过程后，天向陀螺也能被估计出来。且结合图13可以看出，滤波器对三个陀螺添加的0.02（°）/h零偏误差估计效果显著，尤其是天向陀螺的可观测度得到显著提高。

3）通过对比以上两个结论和前文关于可观测性的仿真分析和研究，可以确定本文采用的基于分段线性定常系统的奇异值分解法来研究系统的可观测性得到的理论分析结果与仿真结果和转台实验结论完全对应。

5 结论

本文采用基于分段线性定常系统的奇异值分解法对系统的可观测性进行分析，对飞机静止、起降、匀速飞行、匀加减速飞行、转弯等一系列常规机动条件下系统的可观测性进行了研究，进而实现了滤波器收敛速度和收敛精度的量化分析。通过对静止状态和机动状态下的仿真分析得出的结论与表1得到的结论对比发现，两者的结论完全吻合，再结合转台实验得出的结论，充分说明通过基于分段线性定常系统的奇异值分解法对系统的可观测性进行分析是切实可行的，得出的结论能够为机载惯组在线标校技术的工程应用提供理论支持。