基于地图匹配的车载惯导行进间精对准算法
李 欣,赵海波,马士国
(1.海军研究院空中所, 上海 200436;2.中国人民解放军 91445 部队, 大连 116043)
0 引言
自主导航性和高机动性是保证车载武器系统生存和作战能力的重要因素。自主导航性是指载车具备快速自主定位定向能力,甚至是行进中定位定向的能力,为车载武器提供参考基准,以期实现 “停车就打”,甚至 “边走边打”[1]。为此,车载武器系统往往以高精度惯导为核心构造组合导航系统。高机动性是指载车必须能够快速进入阵地和撤离阵地,而自主导航性又是高机动性的前提,为了提高机动性,导航系统必须具有快速进入工作状态的能力。
为缩减惯导系统初始化所需时间,文献[2]提出了一种基于预置路标点的车载导航系统行进间对准算法。装载该算法的导航系统启动后,只需要进行简单的粗对准后即允许车辆进入行驶状态。车辆路过路标点时认为输入触发信息号给导航系统即可完成系统的精对准,且对准精度高于静基座自对准精度。该算法[2]大幅度降低了导航系统的准备时间,但增加了对预置路标点的依赖。目前,数字地图、捷联惯导和里程仪的组合导航逐渐成为军用车辆自主导航发展的重要方向[3]。但是,对于惯导系统,进入工作状态前必须进行初始对准,而精确性和快速性是惯导系统自对准的两项重要指标[3],所以研究车辆的行进间精度准具有重要意义[4-9]。
本文提出了采用惯导和数字地图匹配技术获取精确的位置信息代替预置路标信息进行行进间精对准的方法。首先研究了基于捷联惯导的地图匹配算法,对文献[3]中提出的基于移动相关的最小二乘地图匹配算法进行了改进,然后研究利用地图匹配结果进行行进间精对准的算法,并通过仿真验证了对准算法的有效性。
1 地图匹配算法
1.1 基于移动相关的最小二乘地图匹配算法
文献[3]针对传统地图匹配算法存在的计算量大、精度不够、易出现误匹配等,以及共同存在的无法消除定位点沿道路方向纵向误差的问题,依据车辆的航位推算轨迹与行驶的真实轨迹相似性原理,同时考虑到地图的数据格式和形式以及编程的可实现、计算的快速性,综合设计了一个充分利用路网信息和行车历史数据的基于惯导的地图匹配算法。该算法是一个部分与整体相结合的匹配算法,分4步进行地图匹配,即:1)预处理;2)路段搜索;3)曲线投影;4)定位修正。文献[3]中曲线投影部分的核心思想是:根据相似性原理和最小二乘原理,拟合出SINS轨迹点(或航位推算点)与对应数字地图点的变换参数平移变换向量T、尺度因子K、旋转变换角α,并依此进行匹配投影。
1.2 匹配算法分析与改进
文献[3]中的实验结果给出了匹配的极限精度(所谓极限精度是指同次实验处理得到的地图数据与定位数据间的匹配精度),与实际应用仍有差距。使用相同路段不同时间数据进行实验,可得如图1所示误差曲线。由图1可知,X方向与Y方向的匹配误差差异较大,X方向匹配后定位误差在0.8m~5.1m,而Y方向匹配后定位误差在0附近波动。因此,考虑对X方向和Y方向分别使用不同尺度因子。

图1 原始方法匹配误差Fig.1 Matching error of original method
根据相似性原理,SINS轨迹与地图轨迹之间存在拉伸、旋转和平移三个维度上的变换。因此,为了更好地匹配精度,这里设尺度变换阵为
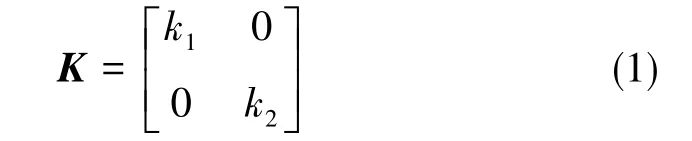
式(1)中,k1和k2分别为X方向与Y方向的变换拉伸尺度因子。
则相似变换后DR定位点为
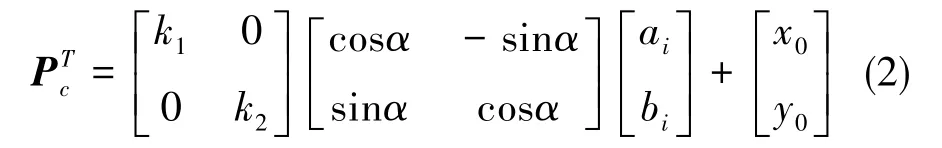
式(2)中,α为轨迹的旋转角度,x0和y0分别为X方向与Y方向的平移参数。
目标函数为
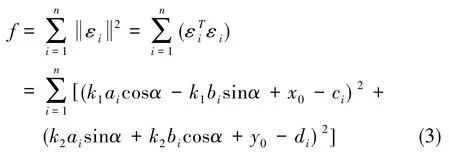
根据最小二乘原理拟合出拉伸、旋转和平移参数,使得f的值最小。所以,分别求f对k1、k2、α、x0和y0的偏导数,并令其等于0,即


上述方程不好求得解析解,故可求数值解。对变换参数方程组采用拟Newton法[10]进行迭代求解,该方法不用求Jacobi矩阵,也不用对矩阵求逆。
1.3 实验验证
为了验证该改进匹配算法的有效性,本文进行了跑车实验,实验条件与文献[3]中基本一致。跑车路线为某环山公路,选用的某型激光SINS陀螺漂移为0.01(°)/h,加速度计零偏为5×10-5g(g为重力加速度),输出频率为50Hz,数字地图精度在米级[11]。使用定位误差优于0.1m的DGPS(差分GPS)作为定位参考标准,这里取3000个SINS采样点进行处理演示,匹配结果如图2所示,匹配误差如图3所示。由图2、图3可知,X方向匹配误差在±3m以内,而Y方向匹配误差依然在0附近波动。经过统计,X方向匹配误差均值从原方法的约3.0m减小到目前的-0.1m,两种方法的匹配误差方差大致相当。因此,根据统计结果可知,改进后的匹配算法比改进前的匹配精度更高。

图2 匹配结果Fig.2 Results of matching
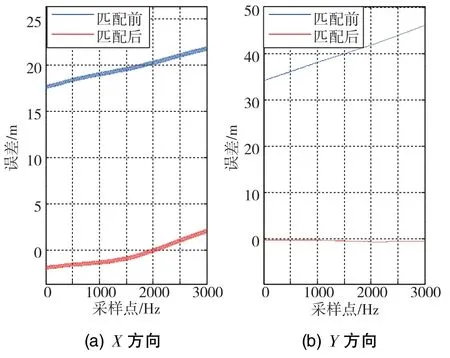
图3 匹配误差分析Fig.3 Analysis of matching error
2 惯导行进间精对准算法
对于惯导系统而言,进入工作状态前必须进行初始对准。精确性和快速性是惯导系统自对准的两项重要指标,但是它们之间常常是矛盾的[12],所以研究车辆粗对准后的行进间精对准具有重要意义。
文献[13]中论述了利用单个路标点进行航向精对准的方法,其原理示意图如图4所示。在行车时间较短、陀螺漂移较小和安装误差角通过标定精确补偿的情况下,根据起始点和路标点间的矢量水平投影ΔSh和航位推算矢量水平投影Δh,给出了航向误差角和里程仪刻度系数误差估计公式
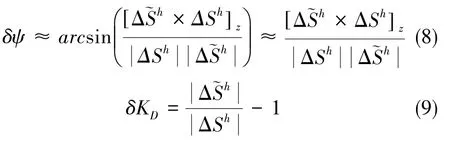
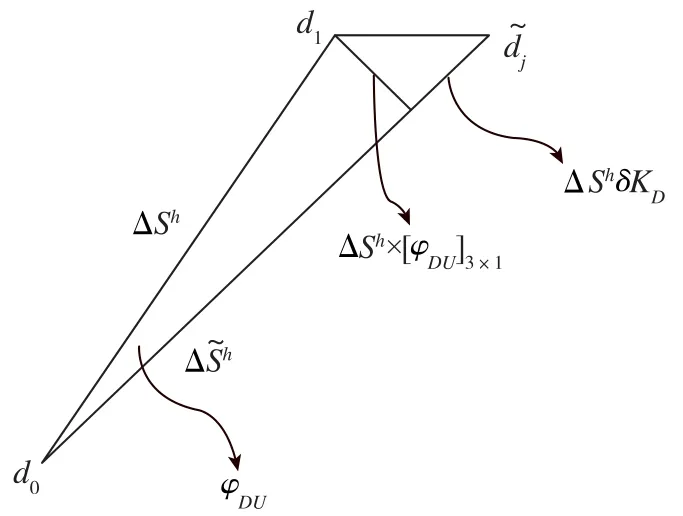
图4 单个路标点对准示意图Fig.4 Diagram of alignment based on single landmark point
跑车实验结果表明,该方法精对准后除去陀螺漂移影响航向误差角约为3′。但是,该方法存在着显著问题:首先必须事先测定好路标点,然后跑车时必须经过该路标点,这对战时的车载武器平台来说很有可能是做不到的。由上一节的实验结果可知,经过地图匹配后能获得若干圆误差在3m以内的定位点,这些定位点就是很好的路标点群,所以这里将地图匹配结果引入辅助精对准。
如图5所示,Pi为无误差真实位置点,i为航位推算位置点,P′i或者Pi为对应的地图匹配位置点,具体是P′i还是Pi是由地图匹配结果决定的。
图5 真实位置与误差位置关系Fig.5 Relationship between error-free positions and errored positions
以P′i为标志点估计出的航向误差角δψ′比以Pi为路标点估计出的δψ大,以Pi为标志点估计出的航向误差角δψ″比δψ小。为了表述方便,这里统一以P′i来表示Pi对应的地图匹配位置点。因此,对于N个地图匹配位置点P′来说,以P′i估计出的航向误差角为

式(10)中,εi基本满足在[-c,c]的对称均匀分布,c为与匹配结果直接相关的常数,所以有

由式(12)可知,以N个地图匹配位置点P′作为路标点进行航向误差角估计的平均值与以N个无误差真实位置点Pi作为路标点进行航向误差角估计的平均值是相当的,这就奠定了以地图匹配结果辅助航向精对准的理论基础。
综上,有误差估计公式

通过式(13)、式(14)估计出的惯导航向角误差δψ与里程仪刻度系数误差δKD都是近似的,补偿后还会有残差。因此,考虑迭代估计的方法以提高精度。
首先,以式(13)、式(14)进行δψ与δKD的初步估计,并以此修正初始时刻的航向角ψ与里程仪刻度系数KD。然后,以保存的N个位置点处的角速度、比力和速度信息重新进行捷联解算与航位推算,以航位推算位置结果再次估计δψ与δKD,并修正ψ与KD。这样,就完成了精对准过程。
利用地图匹配的辅助对准方案的整个流程如图6所示,具体步骤如下:
1)在出发点,快速解析式粗对准;
2)行车6min ~10min,进行地图匹配,获得精确位置信息;
3)估计航向误差角与里程仪刻度系数误差;
4)修正初始时刻的姿态阵、里程仪刻度系数;
5)重新解算,再次估计和修正,对准结束。
为了验证精对准算法,本文进行了数值仿真。主要仿真误差参数设置如表1所示,载车运动轨迹如图7所示。仿真时间为600s,误差估计、修正时间约在第500s。仿真时,假设车辆出发前已经完成解析式粗对准。
仿真实验分成四个对照组:1)单个路标点一次估计,路标点位置精确,零误差;2)单个路标点一次估计,位置误差3m;3)路标点群(即地图匹配辅助)一次估计,位置误差服从(-3m,3m)的均匀分布;4)路标点群迭代估计,位置误差同上。仿真结果如图8所示,参数估计如表2所示。由估计结果可知,地图匹配辅助单次估计精度与单个精确路标点估计精度基本相当,路标点群迭代估计精度最高。
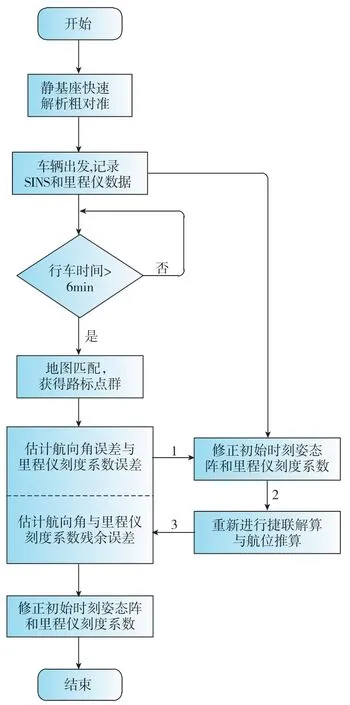
图6 地图匹配精对准流程框图Fig.6 Flowchart of map-matching fine alignment

图7 行车路线图Fig.7 Routine for the vehicle
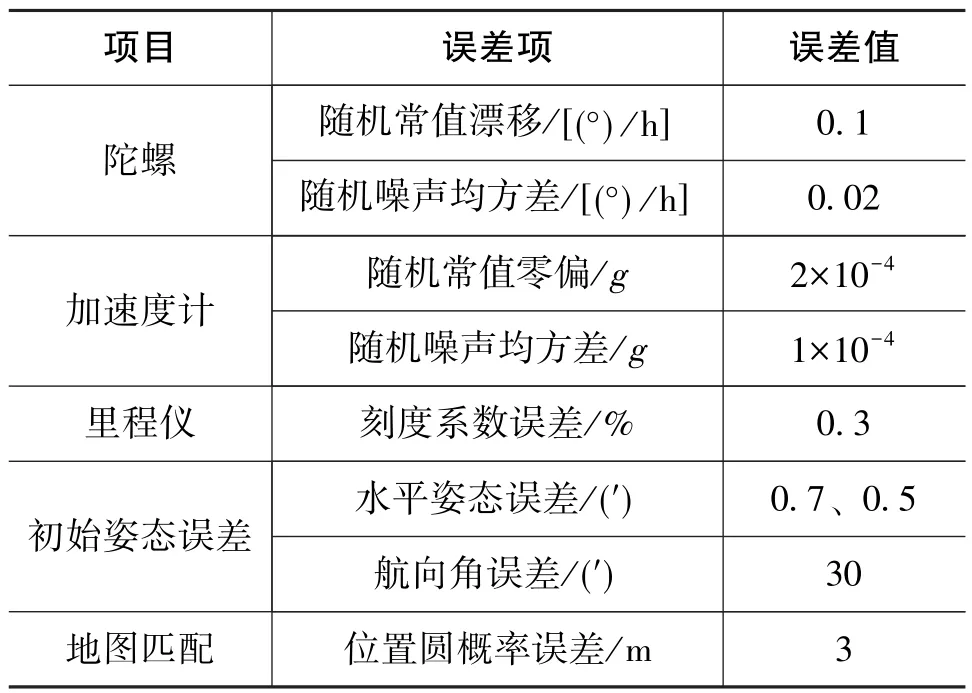
表1 仿真参数设置Table 1 Setting of simulation parameters

图8 四组航向精对准结果对比曲线Fig.8 Comparison of four cases for fine alignment
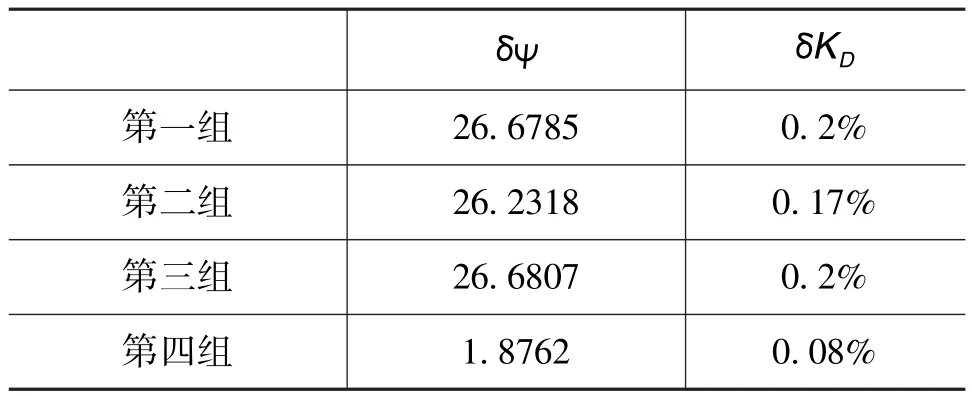
表2 参数估计值Table 2 Estimation for parameters
3 结论
本文提出了一种改进的地图匹配方法,通过两水平方向分别使用不同尺度因子的惯导和地图匹配算法能够改善系统的定位精度,进而提出了利用地图匹配定位结果实现的行进间迭代精对准算法。该算法能够获得与预置路标点行进间精对准方式精度相当的对准结果,从而在不降低精度的前提下摆脱对预置路标点的依赖,有效改善了系统的机动性。

