基于五阶容积-二阶平滑变结构滤波算法的捷联惯导系统初始对准技术
陈 帅,王婉晨,王逸辰,朱 玮
(1.辽宁石油化工大学信息与控制工程学院,抚顺 113001;2.北京航天控制仪器研究所, 北京 100039)
0 引言
捷联惯导系统因其自主性强、隐蔽性好、抗干扰能力强以及其全信息服务等优点被广泛应用于航空、航天、航海等各个领域[1]。初始对准技术是捷联惯导系统的关键技术之一,用于求解惯导系统导航解算过程所需的初始方向余弦矩阵。初始方向余弦矩阵是由初始对准过程得到的初始姿态角和方位角确定的,初始对准过程的时间和对准结果的精度是影响后续导航解算过程的两个非常重要的因素。然而,初始对准时间的减小与对准精度的提高两者之间是矛盾的关系。在一般情况下,初始对准时间越长,初始对准结果的精度才会越高。为了解决这一矛盾,很多学者对此进行了不同方式与方法的改进研究。
为了提高初始对准过程中方位失准角的收敛速度,文献[2]提出了一种快速初始对准方法,该方法采用水平失准角的估计值来计算方位失准角。而为了增加初始对准过程的对准精度,文献[3]建立了东向陀螺漂移的估计模型用于补偿方位失准角的估计精度。但是,这两种方法都依赖于低通滤波器的设计与使用,方位失准角的估计结果对惯性传感器的噪声很敏感[4]。为了解决惯性传感器的未知噪声特性和稳定性问题,很多学者对此做了大量的研究工作,提出了很多新颖的滤波算法,如KF/UPF[5]、CKF[6]、五阶CKF[7]等。即便如此,在精对准过程当中,假设量测噪声满足量测噪声和过程噪声方差值已知的Gauss分布,那么Kalman滤波方法始终是最优的线性估计器[8]。
然而,Kalman滤波对准方法是一种线性滤波方法,其不适用于非线性初始对准过程。二阶平滑变结构滤波方法是一种不需要误差协方差矩阵的预测—校正估计方法[9],其能够克服噪声和干扰影响,是一种简单且实用的鲁棒滤波方法。为了改善捷联惯导系统初始对准过程中方位失准角的对准精度,本文提出了一种基于组合对准结构的二阶平滑变结构滤波对准方法。该组合对准结构将Kalman滤波对准方法和罗经对准方法相结合,构建了一个状态变量与量测变量维数完全相同的初始对准模型,由二阶SVSF来完成对此组合对准模型的状态估计过程。实验仿真结果表明,该方法对准得到的方位失准角对准结果优于一些目前较为常见的初始对准方法。
1 组合对准模型
1.1 误差传递模型
在大方位失准角的非线性模型中,方位失准角的估计误差仍旧是影响导航精度的主要因素。因此,为了改进精对准过程中失准角的估计性能,本文采用了基于Kalman滤波对准方法的非线性误差传递模型。选取当地的东北天坐标系作为导航坐标系,即n系[10]。在n系中,大方位失准角和速度误差方程表示如下

式(1)和式(2)中,φE、φN和φU分别为俯仰失准角、横滚失准角和方位失准角;ωie为地球自转速率;ε和▽为陀螺的常值漂移率和加速度计的常值零偏,下标E、N和U分别代表n系的东北天三个轴的指向;δV为速度误差;g为当地的重力加速度;L为当地的纬度;Re为地球的半径。
为了缩减状态变量、增加量测变量从而使状态变量维数与量测变量维数得到统一,本文实际采用的非线性对准模型为上述对准模型的降阶形式,仅失准角和速度误差作为状态变量,由其构成的状态方程表示如下
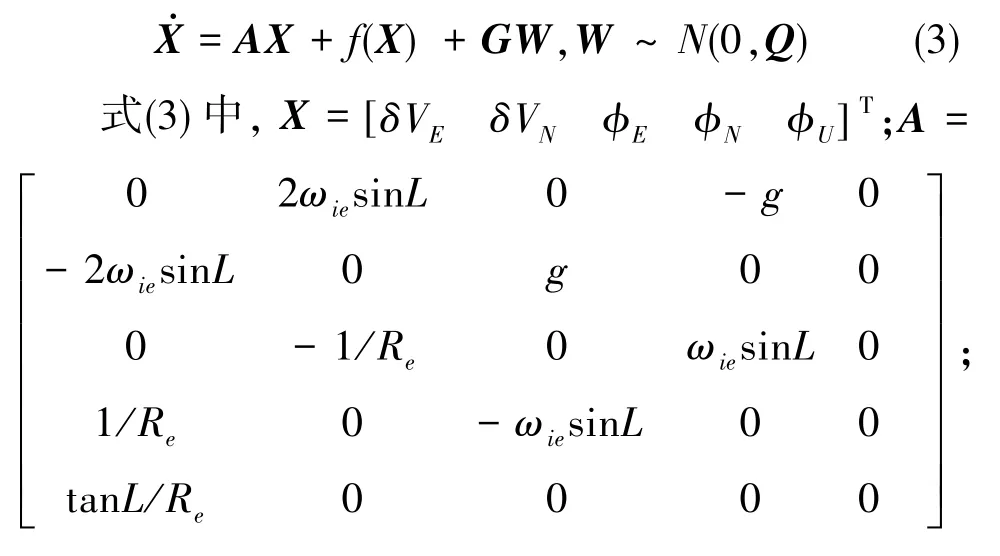

常见的初始对准过程中的零速量测模型表示如下
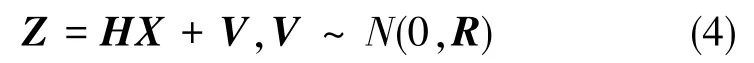
式(4)中,Z=[δVEδVN]T;V=[vEvN]T,V为满足Gauss分布的量测噪声变量,vE和vN分别为东向和北向速度变量的随机误差;H=[I2×2O2×3]为量测转移矩阵。
1.2 罗经对准方法
为了改善一定时间区间内的对准精度,本文采用了变参数罗经对准方法。在静基座的情况下,姿态方程和速度方程可以表示为
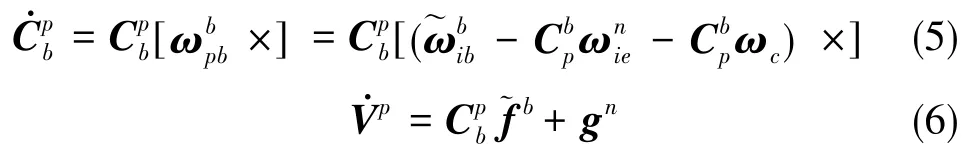
水平罗经环路和方位罗经环路的示意图分别如图1和图2所示。

图1 水平罗经环路示意图Fig.1 Diagram of horizontal compass loop

图2 方位罗经环路示意图Fig.2 Diagram of azimuth compass loop
由图1和图2可知,变量KEi、KNi和KUj(i=1,2,3;j=1,2,3,4)是控制参数,其值可通过式(7)、式(8)计算得到

式(9)中,HE=HN=1,东向速度误差和北向速度误差同时用于计算方位轴的控制角速率,这样图2才能够用于大方位失准角的对准过程。为了缩短对准过程的收敛时间,方位对准环路中需采用一种变参数方法,即
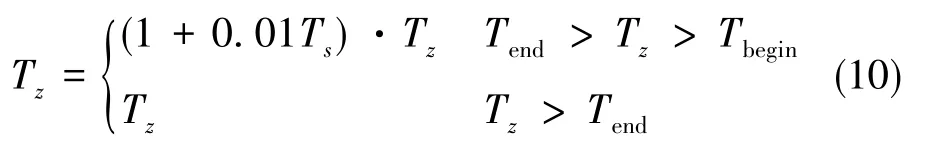
式(10)中,Tbegin为方位罗经对准的起始时间,Tend为确保方位对准角收敛到小角时所需的最长时间节点。当Tz>Tend时,控制参数Ke(s)为零。
1.3 组合对准机制示意图
在捷联惯导系统的初始对准过程中,系统是不完全可观和可控的,因为Kalman滤波方法不能够准确估计惯性传感器的常值漂移,这也就导致了失准角会存在一定的理论误差值。通常,这些传感器的常值漂移可以通过旋转调制技术进行一定的补偿,但旋转调制技术的引入会加大惯导系统的复杂度,而且会引入额外的误差。为了简化系统的复杂程度,减少额外误差的引入,本文提出了一种组合对准方法用于解决因惯导系统不完全可观可控而导致的状态变量可观测度低的问题。该方法在罗经对准进入理论误差范围内后将Kalman滤波模型中的速度量测模型切换到组合过程中的增量模型,该增量模型的量测状态由速度误差、姿态角误差和方位角误差构成。
为了实现这一组合对准过程,有两点是需要明确知道的。第一点就是增量量测模型的建立是为了实现完全可观测模型的构建,增量量测模型采用三个失准角和水平速度误差作为量测状态,从而构成了五维量测模型。其中,三个失准角可以通过在同一时间节点下求得的Kalman滤波方法中未补偿的方向余弦矩阵与罗经对准方法中补偿后的方向余弦矩阵乘积并求解得到。失准角的计算过程可以按式(11)和式(12)来进行求解

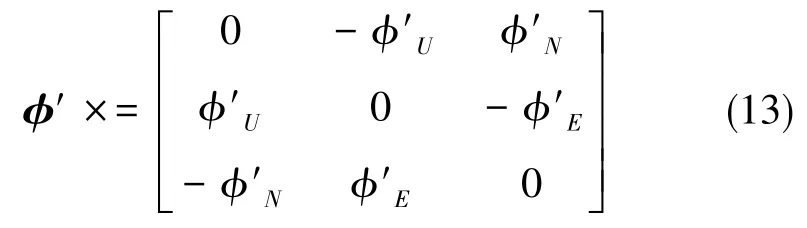
因此,增量量测模型可以用式(14)来表示

式(14)中,Z∗=[δVEδVNφ′Eφ′Nφ′U]T,V∗=[vEvN0 0 0]T,H∗为一个5×5的单位矩阵。所以,由式(5)和式(14)便可构成完全可观测的组合对准模型。由于在大方位失准角对准过程中,方位失准角不能同小失准角一样进行线性等效,因而需要通过姿态矩阵来进行姿态的计算。
实现组合过程的第二点就是切换时间的选择。Kalman滤波对准方法收敛到理论精度的速度要比罗经对准方法快,为了得到更加准确的量测值就需要选择罗经对准结果进入理论精度区域后的时间作为两种方法的组合时间。组合对准机制流程图如图3所示。
在图3中,Kalman滤波对准方法和罗经对准方法同时运行。t1为水平角对准时间,t2与t3之和为方位角对准时间。t2时间段为方位角稳定阶段,即罗经对准结果收敛到理论精度范围内的阶段。在方位角稳定之后,式(4)切换到式(14),由式(3)和式(14)来完成后续的组合对准过程。
因为两种对准方法的方位失准角的理论精度计算不尽相同,作为量测状态变量的方位失准角误差与状态变量的方位失准角误差在组合过程中会部分抵消。因此,组合对准得到的方位失准角估计值略优于常规对准方法。
2 五阶容积-二阶平滑变结构方法
二阶平滑变结构滤波方法在其预测更新过程中是一个预测-校正的形式。在预测过程中,先验状态估计通过k时刻的系统先验知识来进行计算。在更新过程中,计算得到的先验估计值用来产生后验状态估计值。在这种方法中,校正增益用于将估计的状态和其一阶导数限制在滑动超平面的临近区域,这个临近区域也就是其存在子空间。为了便于描述二阶平滑变结构滤波过程,假设通过离散时间状态转移模型表示的一类非线性系统为

图3 组合对准过程示意图Fig.3 Schematic diagram of integrated alignment process
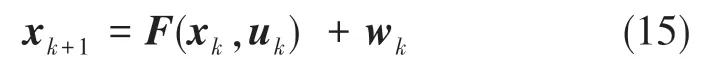
式(15)中,F:Rn+p→Rn为非线性状态转移函数,xk+1∈Rn×1为状态变量,uk∈Rp×1为控制变量,wk∈Rn×1为过程不确定变量。假设量测方程为线性或分段线性的,那么其可具体表示如下
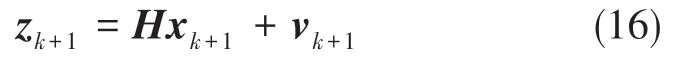
式(16)中,zk+1∈Rm×1为量测变量,vk+1∈Rm×1为量测噪声,H∈Rm×n为一个已知的正对角线或伪对角线测量矩阵。
二阶平滑变结构滤波算法是针对线性系统进行设计的,为了解决该系统的非线性问题,本文提出采用五阶容积规则进行一步预测,从而构建成了五阶容积-二阶平滑变结构滤波算法,该算法在非线性系统中的应用主要可归纳为以下5个步骤[10]:
1)由系统的状态转移矩阵得到的先验状态估计向量的预测为
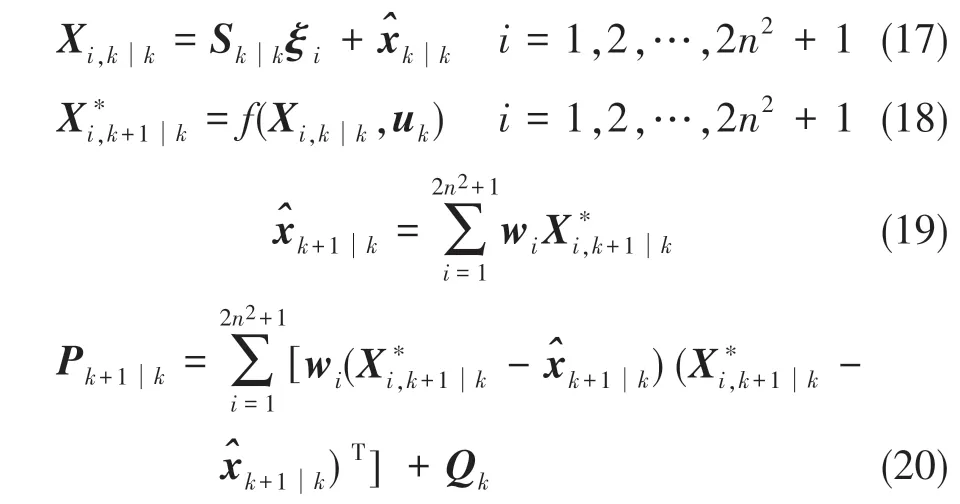
其中,容积点和权重表示如下

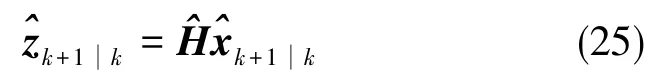
式(25)中,为准确的量测模型H的估计。
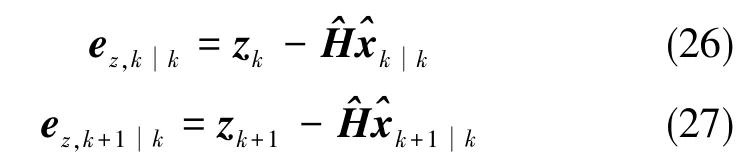
3)二阶平滑变结构滤波算法校正增益向量Kk+1∈Rn×1可通过一个包含了先验量测误差、后验量测误差和前一时刻的后验量测误差的函数来表示

式(28)中,为量测矩阵的伪逆。假设初始时刻所有状态是可测的,那么和H在初始时刻就是方阵,。γ=diag(γii)∈Rm×m为一个对角矩阵,其对角元素满足0<γii<1。

5)在每个采样时间点进行步骤1~步骤4的迭代重复就是整个算法的具体实现过程,需要特别说明的是后续的迭代过程中,需要将作为来使用。
3 仿真验证
3.1 仿真参数
初始对准过程的仿真参数如表1所示。一般地,大方位失准角不会超过15°,因此将初始方位失准角设为15°,水平失准角设为1°。
常规非线性Kalman滤波方法(UKF、CKF和五阶CKF)的初始参数如下所示:



表1 仿真参数Table 1 Simulation parameters

五阶容积-二阶平滑变结构滤波算法的初始参数表示如下:


3.2 仿真结果与分析
仿真过程持续600s,五阶容积-二阶平滑变结构滤波算法可以通过图3中的组合对准方法来实现。组合对准过程开始于200s之后,失准角误差曲线如图4~图6所示。
在图4中,很明显俯仰失准角误差不是最小的,但却是稳定的。同样的现象在图6中也可以看到,而且在所有估计方法中,其方位失准角误差是最小的,方位失准角误差是精对准过程的关键。因此,五阶容积-二阶平滑变结构滤波对准方法能够较好地解决大方位失准角对准问题。
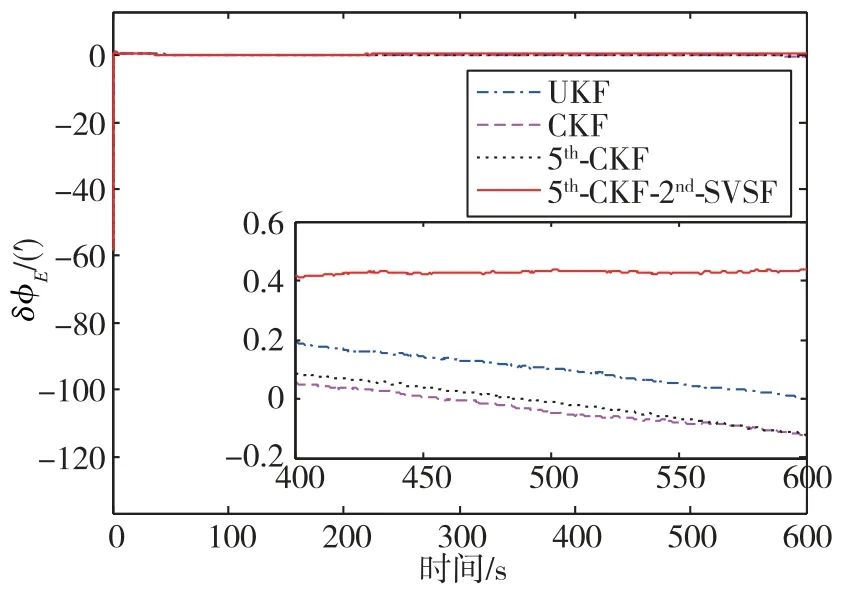
图4 俯仰失准角估计误差曲线Fig.4 Estimation error curves of pitch misalignment angle

图5 横滚失准角估计误差曲线Fig.5 Estimation error curves of roll misalignment angle

图6 方位失准角估计误差曲线Fig.6 Estimation error curves of azimuth misalignment angle
为了表明五阶容积-二阶平滑变结构滤波算法的有效性,在误差测量条件下进行了100次Monte Carlo仿真模拟,均值和标准差如表2和表3所示。

表2 估计误差均值Table 2 Mean of estimation errors

表3 估计误差标准差Table 3 Standard deviation of estimation errors
从表2可以看出,五阶容积-二阶平滑变结构滤波方法的水平对准误差不比其他方法的结果更好,但是其方位失准角估计精度明显比其他几种方法高。表3中的标准差表明了估计结果的稳定性,同时也说明了本文提出的方法具有更好的重现性。总之,五阶容积-二阶平滑变结构滤波方法能够用于捷联惯导初始对准过程中,并且能够得到很好的估计精度和稳定的估计结果。
4 结论
本文提出了一种五阶容积-二阶平滑变结构滤波对准方法,该方法提高了大方位失准角对准过程中方位失准角的对准精度。五阶容积-二阶平滑变结构滤波方法需通过Kalman 滤波对准方法和罗经对准方法组合的方式才能得以实现。五阶容积-二阶平滑变结构滤波是一个鲁棒估计方法,仿真结果表明该方法比其他常规对准方法有更好的估计精度。此外,需要特别指出的是,五阶容积-二阶平滑变结构滤波对系统构成还有其特殊要求,即系统状态变量维数与量测变量维数要相同,且要求系统完全可观和可控。本文通过组合对准方法和量测模型的切换,很好地解决了其在捷联惯导系统初始对准中的应用这一问题。

