双星编队对空间非合作目标的仅测角跟踪方法

姚培东，李星秀，吴盘龙，苏 鼎

（1.南京理工大学自动化学院， 南京 210094；2.南京理工大学理学院， 南京 210094；3.中国人民解放军 66483 部队， 北京 100093）

0 引言

随着全球太空资源开发的提高和未来太空作战趋势的加剧，越来越多的国家拥有了进入太空和利用太空的能力，太空变得更加具有竞争性和对抗性。其中，空间监视系统可以监视空间目标的运行，确定潜在的威胁，还可以预测空间目标的轨道，其水平的高低直接制约着空间对抗能力的发挥［1］。同时，空间监视系统相比地面监视系统具有全天候、视场广、不受大气环境影响等特点，发展天基监视系统就显得尤为重要。

天基观测平台上获取目标信息的方式包括有源主动和无源被动两种［2］。其中，无源被动的工作方式隐蔽性好、作用距离远，具有重要的实用价值，但是此种方法只能获得目标的角度测量信息，定位精度不高。为了提高定位精度，一些学者［3-4］通过引入改进的迭代扩展Kalman滤波（Iterated Extended Kalman Filter，IEKF）和迭代扩展Kalman粒子滤波（Iterated Extended Kalman Particle Filter，IEKPF）来增加迭代次数。虽然能提高定位精度，但是这种方法计算量太大，实时性很难满足，当测量误差较大时，效果反而更差。文献［5］通过将初定轨（Initial Orbit Determination，IOD）和序贯估计相结合，利用改进的Laplace法，通过在一定时间内利用更多组测量信息提高初定轨的精度用于序贯估计。但是，这种方法需要在短时间内获取更多组测量值，对系统硬件要求很高，且单个平台对空间目标光学测角定轨可观度和几何约束较差，当目标与观测星的距离较远时，短弧段的测量序列随时间变化近似线性，Laplace方程接近病态，造成定轨偏差较大。因此，该方法不适合跟踪远距离的目标。为了解决此问题，文献［6］通过对目标长时间的观测数据采集，选取不同的可观测弧段进行数据融合，间接改善了观测几何条件，使定轨精度提高。但是，这种方法需要长时间采集数据，实时性也比较差，且量测模型没有考虑坐标转换，虽然公式简单，但是实用性不强。

针对上述问题，结合现有分布式卫星快速发展的背景，利用编队卫星对目标进行多视线测量，改善观测的几何条件，融合观测数据，在保证实时性的同时，提高了对非合作目标的跟踪精度和稳定性。此外，受空间几何因素和光学因素的影响［7］，利用光电传感器对目标进行观测时会出现某段时间内测量值丢失和测量值误差过大的现象，这些测量故障会造成跟踪精度不高甚至跟踪结果发散。基于此设计自适应滤波，该滤波基于新息构建自适应因子，设计增益调节矩阵，提高了滤波的鲁棒性。最后，通过仿真对提出方法的有效性进行了验证和分析。

1 空间目标状态模型

如图1所示，在理想情况下，卫星和地球组成一个二体系统，卫星沿固定的轨道围绕地球运动。但实际情况下，卫星在围绕地球运动的过程中会受到很多干扰，其中最主要的是地球非球形引力摄动、大气阻力摄动、日月引力摄动、太阳光压摄动等。不同高度轨道的卫星所受的摄动影响不同，本文选取的非合作目标运行在高度较低的轨道，因此所受的主要摄动为地球非球形引力摄动。

图1 卫星编队非合作目标跟踪系统Fig.1 Satellite formation for NCST tracking system

在仅考虑地球J2摄动时，卫星的轨道方程如下

式（1）中，f为地球非球形J2摄动下所产生的加速度。f在地心惯性坐标系（Earth Centered Inertial，ECI）下可表示为［6］

则式（2）可改写为

式（1）～式（5）中，r＝［xyz］T为卫星在ECI下的位置矢量；为卫星在ECI下的速度矢量；为卫星距地心的距离；μ为地球引力常数，其值为3.986×1014m3/s2；J2为二阶带谐项系数，其值为1.08263×10-3；Re为地球赤道半径；k＝［0 0 1］T。

将r和v定义为状态矢量，即X＝［r；v］，则式（1）可写为

式（6）离散化后可进一步写为

利用Euler法对式（7）进行求解

式（8）中，Δt＝tk+1-tk，wk为过程噪声矩阵，假定Gauss白噪声均值为0，协方差为Qk。

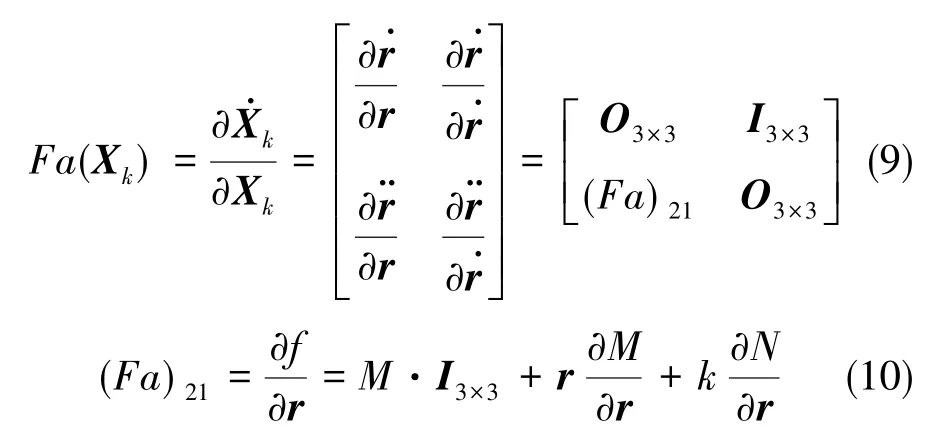
2 测量模型

2.1 观测方程中的坐标转换

在典型的仅测角无源定位中，方位角和高低角的计算定义为目标与观测器位置矢量之差。以往的文献多是直接在ECI下建立观测方程，公式简单，但是观测数据是在主星和从星各自的轨道坐标系下测量的，而双星观测器和目标的位置矢量都建立在ECI下，而且需要建立编队双星之间的坐标关系。因此，需要进行坐标转换才更接近真实系统，Euler角的坐标转换如图2所示。

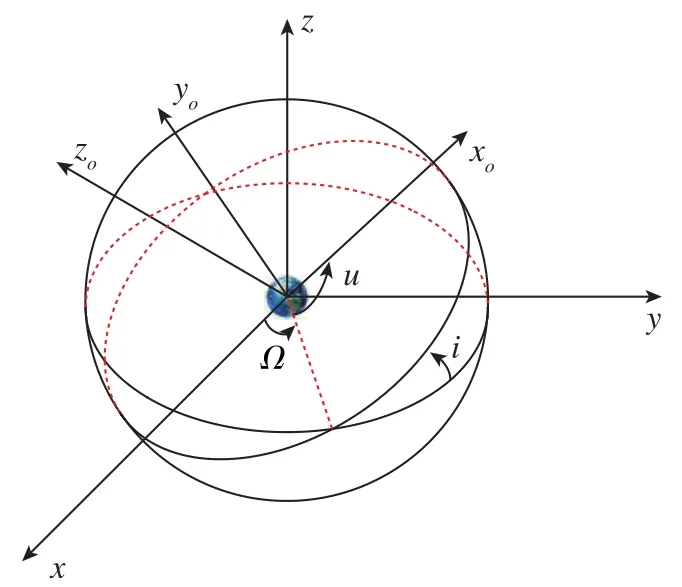
图2 Euler角坐标转换示意图Fig.2 Schematic diagram of Euler angles coordinate transformation

式（11）中，Gi为坐标转换矩阵。以观测主星为例，G1＝R3（u）R1（i）R3（Ω），Ω、i、u分别为观测主星的升交点赤经、轨道倾角和纬度幅角［8］，R3（Ω）、R3（u）为绕z轴旋转角度Ω和u的变换矩阵，R1（i）为绕x轴旋转角度i的变换矩阵，其矩阵形式为

2.2 目标运动观测方程

设观测主星对目标测得的高低角和方位角分别为αk1、βk1，观测从星对目标测得的高低角和方位角分别为αk2、βk2，其定义如下

式（13）中，ηα1、ηα2为高低角的测量噪声，ηβ1、ηβ2为方位角的测量噪声。

将获得的方位角和高低角投影到观测主星和观测从星的轨道坐标系下，则测量值可表示为

从星的测量值通过星间链路传输给主星，zk2为目标在从星轨道系下的量测值，应转换到主星轨道系下。将zk2从从星轨道系转换到ECI，其坐标转换矩阵为；再从ECI转换到主星轨道坐标系，其坐标转换矩阵为G1。因此，为从星轨道坐标系到主星轨道坐标系的转换矩阵。最终，双星编队对非合作目标的量测值为

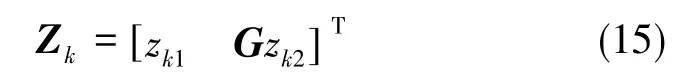
观测双星对目标的观测量均为单位矢量，故量测方程的右端也应为单位矢量。在惯性坐标系下，观测双星到NCST的单位观测矢量为

式（15）建立在主星轨道坐标系下，式（16）建立在ECI下。为了方便滤波时协方差矩阵等的获取，需进行坐标转换，最终可写为

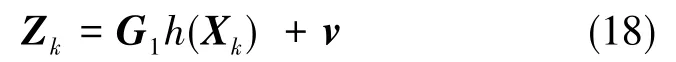
式（18）中，v为测量噪声矢量。假设为Gauss白噪声序列，其均值为0，协方差为Rk。

3 跟踪滤波算法

3.1 平方根容积Kalman滤波

天基仅测角跟踪是非线性状态估计，平方根容积Kalman滤波（Square Root Cubature Kalman Filter，SRCKF）使用基于容积规则的数值积分方法直接计算非线性函数的均值和方差，只需计算函数值，避免求导计算。同时，SRCKF利用协方差的平方根直接参与递推运算，确保了协方差矩阵的对称性和正定性，能保证滤波的精度和稳定性。

SRCKF滤波的步骤如下：

（1）初始化

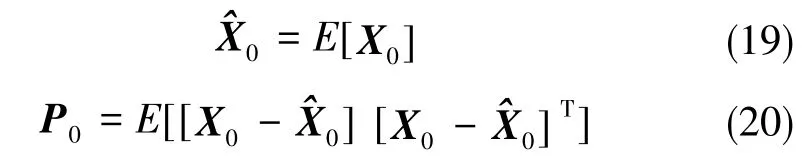
（2）时间更新

计算容积点，有

式（21）中，N＝2m，m为状态的维数；S0＝chol（P0），即。记m维单位向量为e＝［1 0 … 0］T，使用符号［1］表示对e的元素进行全排列和改变元素符号所产生的点集，称为完整全对称点集。

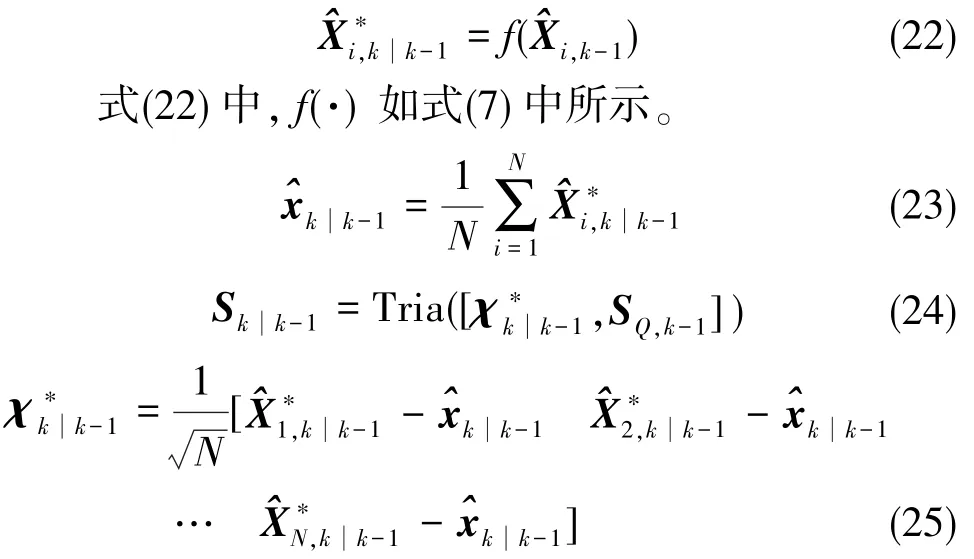
（3）量测更新

3.2 自适应SRCKF

在复杂的太空环境中，由于地球遮挡等几何因素、目标辐射强度以及目标背景较亮等影响光电传感器工作的光学因素，难免会出现量测信息不准确或者信息传输的暂时中断，导致不能提供正确的量测信息。此时，传统的Kalman滤波精度会大大降低，甚至导致滤波发散。因此，需要设计自适应滤波来提高其鲁棒性。自适应滤波一般是基于新息和基于残差设计的［9-10］，本文采用的是基于新息的方法来设计自适应平方根容积Kalman滤波（Adaptive Square Root Cubature Kalman Filter，ASRCKF）。

自适应滤波通过采集过去一定时间的新息，利用采集到的新息实时调整滤波器的误差矩阵［11-12］。具体调整策略是通过比较实时估计的矩阵值和设定的矩阵值，当相差大于一定的阈值时就进行调整。

真实测量值和一步预测值计算的残差公式如下

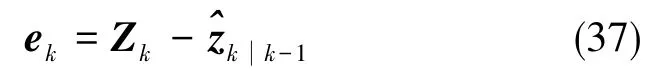
式（37）中，Zk为k时刻的真实测量值，为k时刻的量测估计值。

若系统量测的真实误差统计特性与滤波递推误差模型一致时，以下等式成立

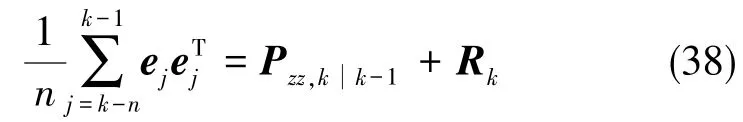
式（38）中，n为滑动窗口宽度，表示历元新息值的采集个数。

当量测异常时，量测噪声与滤波递推模型不符，需要引入一个由比例因子组成的自适应矩阵Sk到算法中来调整测量协方差矩阵和让理论值接近真实值，关系式如下

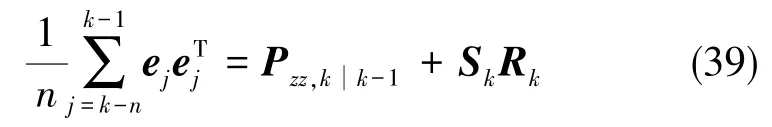
其中，式（39）左边为实际的新息协方差，右边为经调整后的理论新息协方差，则Sk可推导如下

由以上公式可知，当测量噪声异常时，Sk是一个单位矩阵，对滤波无影响。当量测出现异常时，由比例因子组成的自适应矩阵对应的项将变得相对更大，会消除测量值异常的影响。

矩阵Sk在计算过程中，由于误差等因素的影响，其对角线元素可能小于1或者为负数。然而，自适应矩阵Sk不能有元素小于1，故需要对自适应矩阵做进一步处理

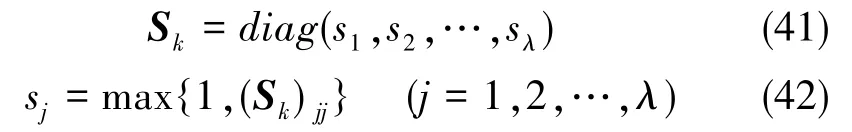
（Sk）jj为Sk的第j个主对角线元素，当量测噪声突变时，会对滤波增益产生影响，式（34）变为

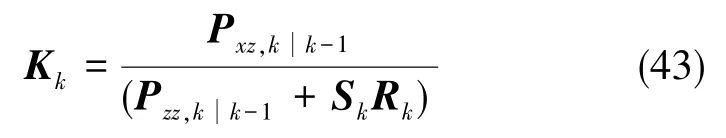
4 仿真验证

观测双星编队平台处于高轨道，非合作目标卫星处于低轨道，编队卫星和目标卫星的初始轨道参数如表1所示。其中，a为轨道半常轴，e为偏心率，i为轨道倾角，Ω为升交点赤经，ω为近地点幅角，f为真近点角。

表1 编队卫星和空间非合作目标初始轨道参数Table 1 Initial orbit parameters of satellite formation and NCST

利用STK11卫星仿真软件高精度轨道预报模型（High-precision Orbit Propagator，HPOP）生成NCST的星历作为标称数据，生成观测双星的星历作为双星的状态量，利用Access功能产生仿真的数据弧度，可得到一天之内非合作目标对观测编队卫星的可见时间表。本文选定仿真时间为2019年3月11日07：56：50～09：03：23约4000s，采样间隔为1s。

仿真的初始状态矢量X0＝［-6535.038km-2142.106km 2329.429km-0.730km/s-4.327km/s -5.905km/s］，初始状态误差P0＝diag（25km，25km，25km，10m/s，10m/s，10m/s），方位角和高低角测量误差均为0.0001rad，其他的仿真参数在上文已给出，仿真结果如图3所示。

图3 空间非合作目标状态估计误差Fig.3 State estimation error of NCST

表2给出了两种跟踪方法的状态估计均方根误差（Root Mean Square Error，RMSE）结果对比，Monte Carlo仿真次数为100次。从结果中可以看出，在相同的仿真条件下，相比单星跟踪，双星跟踪的收敛位置误差减少了27.06%，收敛速度误差减少了26.96%。

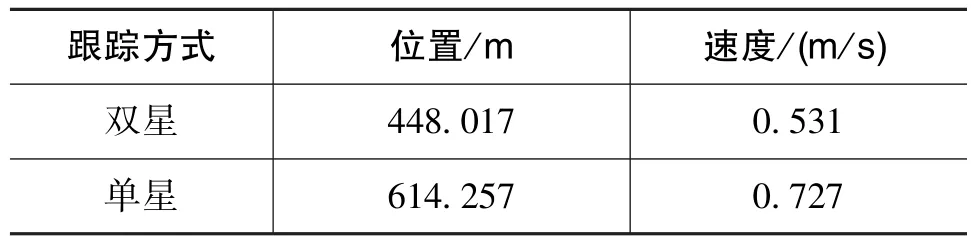
表2 两种跟踪方法均方根误差对比Table 2 RMSE comparison of two tracking methods

4.1 量测故障

为了验证所设计的自适应滤波算法的性能，跟踪方式为双星跟踪，分别给出如下两个算例。

算例1：在保持以上仿真条件不变的基础上，模拟测量数据丢失的场景。在历元2000s～2050s，方位角和高低角输出都设置为0，ASRCKF和SRCKF的仿真结果如图4、图5所示。

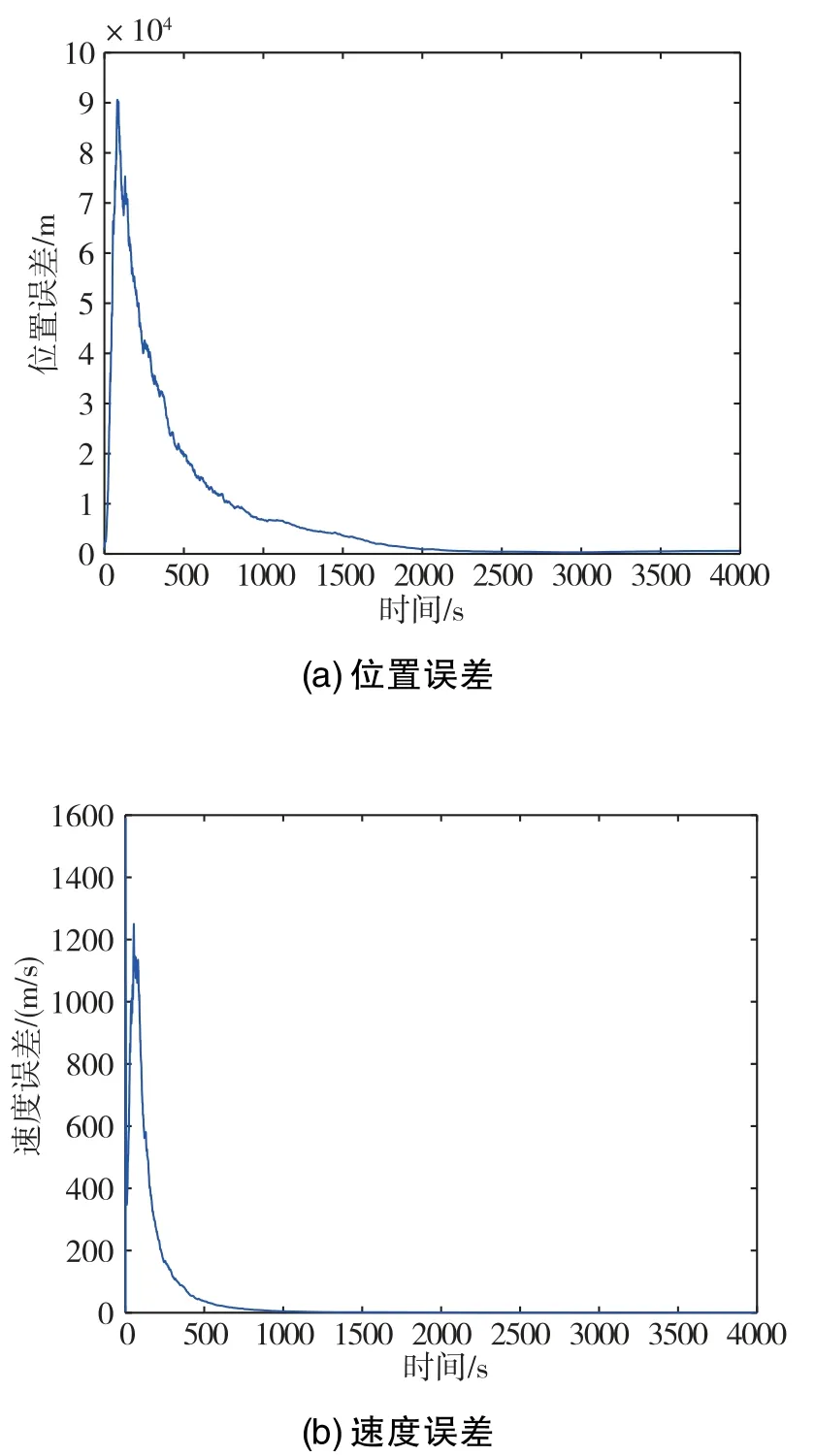
图4 算例1下的ASRCKF状态估计误差Fig.4 State estimation errors of ASRCKF in case1

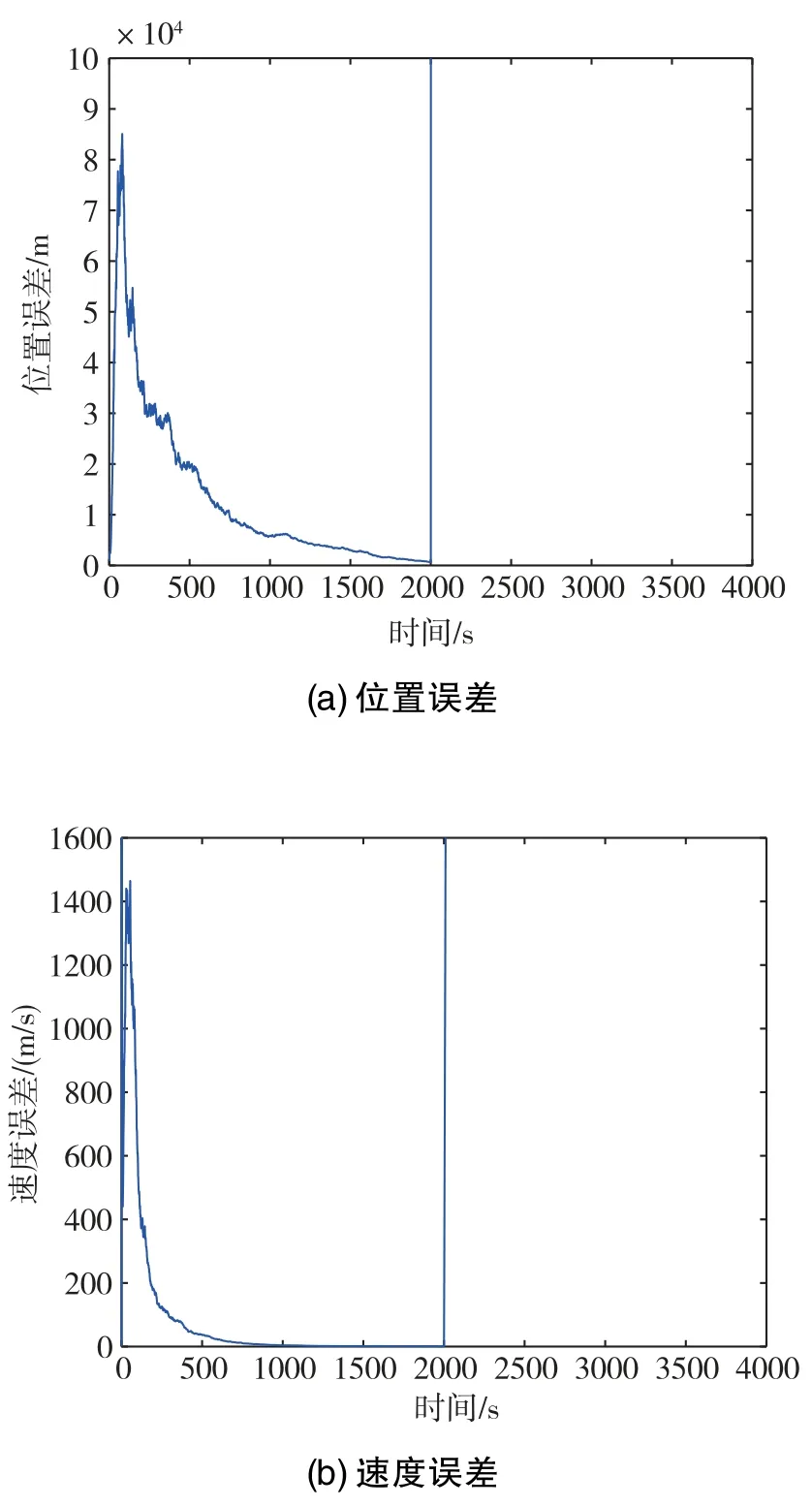
图5 算例1下的SRCKF状态估计误差Fig.5 State estimation errors of SRCKF in case1

算例2：模拟测量数据不准确时的场景。在历元2500s～2510s 高低角和方位角的角度测量基础上加入0.0004rad的常值粗差，ASRCKF和SRCKF的仿真结果如图6、图7 所示。

图6 算例2下的ASRCKF状态估计误差Fig.6 State estimation errors of ASRCKF in case2

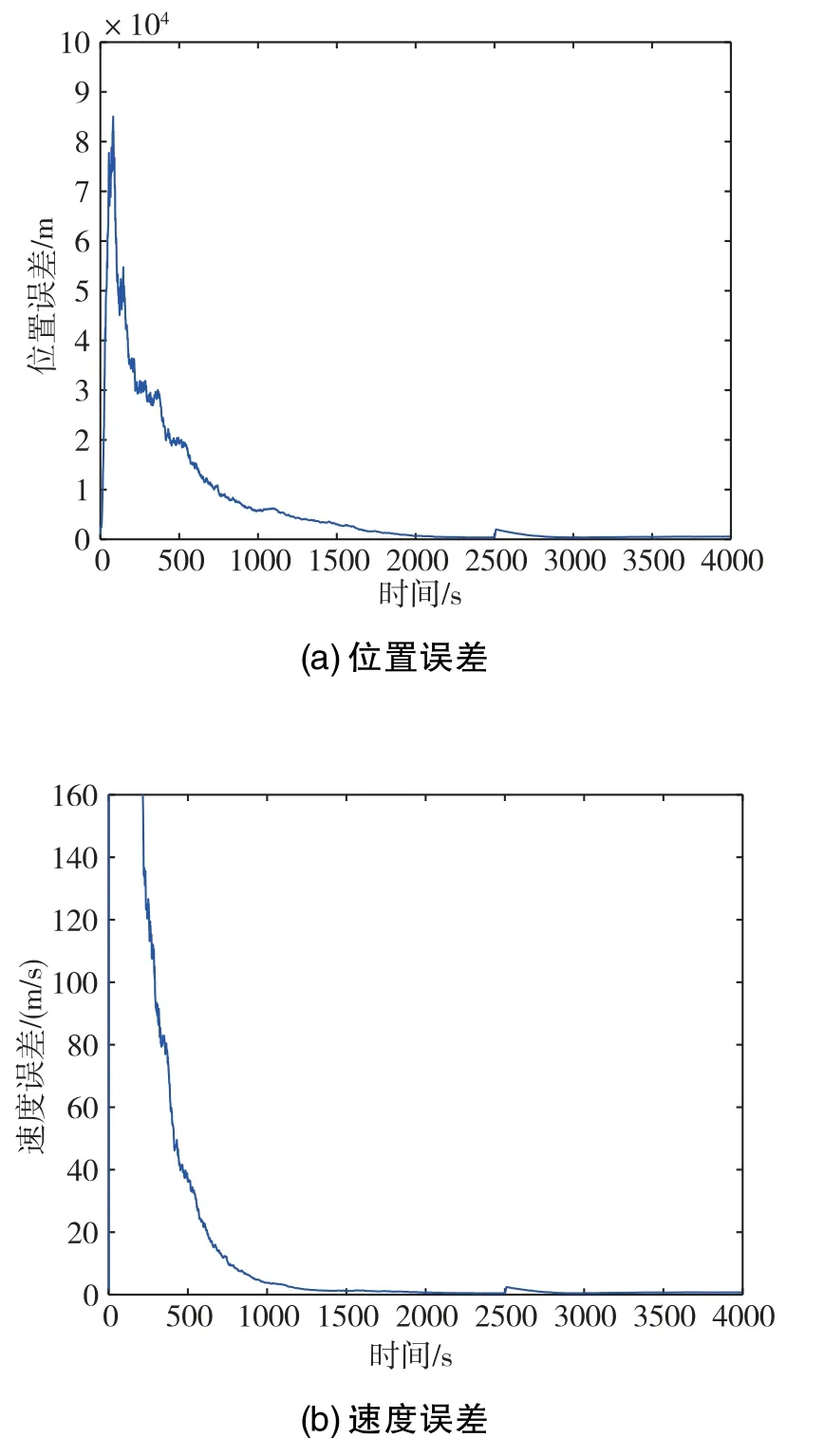
图7 算例2下SRCKF状态估计误差Fig.7 State estimation errors of SRCKF in case2

在此基础上求解两种滤波算法的均方根误差，如表3 所示。

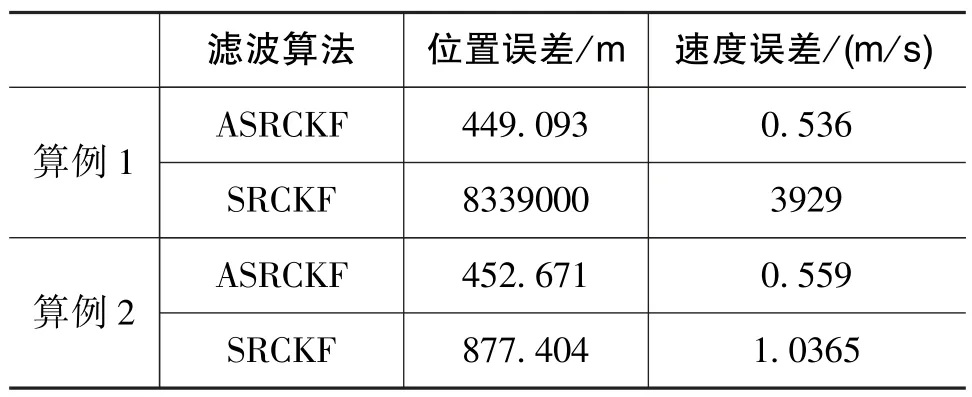
表3 两种滤波算法均方根误差对比Table 3 RMSE comparison of two filter algorithms

对比表2和表3中算例1的数据可以看到，当出现量测缺失扰动时，自适应滤波结果几乎无变化，依然能够不受量测异常扰动的影响。滤波结果趋于平稳，而常规滤波则直接发散，滤波结果不正确。

对比表2和表3中算例2的数据可以看到，ASRCKF面对量测值不准确扰动时，滤波结果出现小幅度范围的波动，但是和正常量测相比，滤波结果变化不大且很快重新收敛；而SRCKF则出现了较大的波动，滤波精度较差，虽然最终依然能够收敛，但是需要较长的时间。

5 结论

本文提出了一种双星编队对非合作目标的仅测角跟踪方法，建立了跟踪的状态模型和量测模型，利用ASRCKF滤波算法进行状态估计，并且完成了不同量测条件下的仿真估计。仿真结果表明，双星编队的联合跟踪相比单星具有更高的跟踪精度，位置误差和速度误差分别减少了27.06%和26.96%。针对量测异常的情况，ASRCKF相比SRCKF能够很好地抑制量测异常扰动对滤波结果的影响。本文提出的方法在实际应用中还存在一定的局限性，例如双星编队量测数据不同步对跟踪精度的影响、测量角度象限的跳变对跟踪精度的影响，这些问题都需要后续进一步研究解决。