局部紧的阿贝尔群上谱测度的几何结构

买买提艾力·喀迪尔，范琼，2，阿里米热·阿布拉

(1.喀什大学数学与统计学院，新疆 喀什 844000；2.华中师范大学数学与统计学学院，湖北 武汉，430079)

0 引言

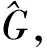
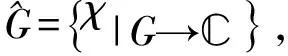
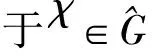
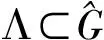
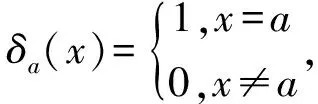
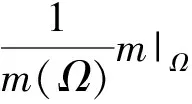
在任何局部紧的阿贝尔群G上，甚至在有限群上可以讨论谱集猜想[2].在欧式空间Rd，谱集猜想的研究取得了一些局部性的结果[3-4]，已知一般谱集猜想在维数d≥3的时候不成立[5-7].但迄今为止，谱集猜想在一维或者二维空间上是否成立仍不清楚.

1998年，文献[8]发现了第一类奇异、非原子的谱测度.这一类奇异测度中，最简单的情形是四分Cantor分形测度μ4，也被称作伯努利卷积.从此以后，一大批数学家在这一领域进行研究，取得了有意义的研究结果[9-14].

本文将欧式空间Rd上有关谱对(μ，Λ)的研究推广到一般的局部紧的阿贝尔群G上任意概率测度对(μ，ν)上，主要研究局部紧的阿贝尔群G上测度的谱性质与其卷积测度的谱性质之间的关系，同时研究G上谱测度的几何结构.在欧式空间d上的相关研究可以参阅文献[14-16].

1 预备知识

将谱对的概念推广到任意概率测度.设μ是G上的一个Borel概率测度，L2(μ)是平方μ-可积函数空间所构成的Hilbert空间，亦即

在空间L2(μ)上的内积和范数分别定义为

称(μ，ν)为一个谱对，当且仅当Fμ，ν：L2(μ)→L2(ν)是一个酉算子，亦即等距到上映射.

根据定义1，(μ，ν)是一个谱对，当且仅当(ν，μ)是一个谱对.根据等距算子的定义，

‖Fμ，ν‖L2(ν)=‖f‖L2(μ).

(1)

等式(1)等价于对任意f1，f2∈L2(μ)，有

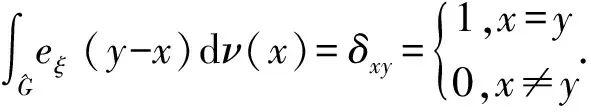
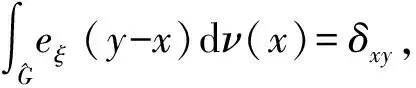
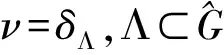
定义3 设μ是群G上的Borel概率测度，则其Fourier-Stieltjies变换定义为

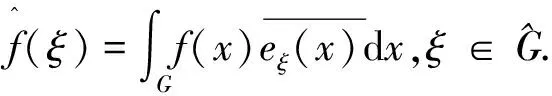
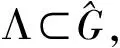
则以下说法是等价的：

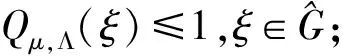
2 主要结论及其证明

定义4 设X是一个度量空间，A⊂X是一个非空集合.如果对任意a1，a2∈A，0<α<1都有

αa1+(1-α)a2∈A，

那么称集合A为凸集.

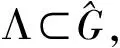
另一方面，对于μ∈M，定义：

注1 根据引理1，若μ∈M⊥(Λ)，则{eλ}λ∈Λ是空间L2(μ)上的规范正交系.若μ∈MONB(Λ)，则{eλ}λ∈Λ是空间L2(μ)上的规范正交基，亦即(μ，Λ)是一个谱对.集合MONB(μ)是测度μ的所有谱组成的集合.

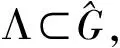
证明设μ，ν∈M⊥(Λ)，并且0<α<1，由Fourier变换的线性性可得

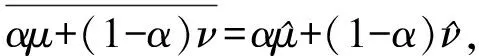
所以

根据Cauchy-Schwarz不等式，有

(2)

从而，根据μ，ν∈M⊥(Λ)和不等式(2)，得到

故集合M⊥(Λ)是一个凸集.

为了证明集合MONB(Λ)不是凸集，对于μ，ν∈MONB(Λ)，0<α<1，考虑

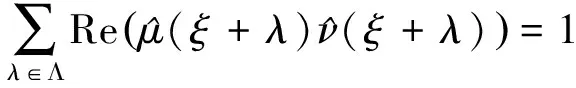
不成立.因此，一般的情况下有不等式

故集合MONB(Λ)不是凸集.

对于μ，ν∈M，令μ⊗ν表示乘积空间G×G上的乘积测度，即对于集合A×B⊆G×G，有

(μ⊗ν)(A×B)=μ(A)·ν(B).

对集合A⊆G，定义A+={(x，y)∈G×G|x+y∈G}.如果A⊆G是一个Borel集，那么A+是G×G上的一个Borel集.

定义5[18]设μ，ν∈M，A⊆G是一个Borel集，则测度μ和ν的卷积定义为

(μ*ν)(A)=(μ⊗ν)(A+).

测度的卷积有如下性质[18]：

(1) 若μ和ν是概率测度，则μ*ν也是概率测度；

定理2说明在一般情况下，群G上的两个谱测度的卷积测度不一定是谱测度，而定理3说明对测度附加一定条件之下，两个谱测度的卷积测度还是谱测度.

定理2 设μ1，μ2是G上的两个概率测度，且都不是Dirac测度，令μ=μ1*μ2.若{eλ}λ∈Λ是空间L2(μ1)上的一个正交系，则{eλ}λ∈Λ也是L2(μ)上的正交系，但不是L2(μ)上的正交基.

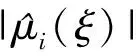
由引理1，{eλ}λ∈Λ是空间L2(μ)上的正交系，但不是L2(μ)上的正交基.

定义6 设A，B，C是G上的3个离散集合.如果对于任意a∈A，存在唯一一对(b，c)∈(B×C)使得a=b+c，那么称集合A是集合B和集合C的直和，记为A=B⨁C.

(1) (μ，Λ)和(ν，Γ)分别是两个谱对；

那么卷积测度μ*ν是以Λ⨁Γ为谱的谱测度.

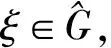
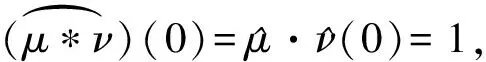
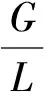
显然Zd是欧式空间Rd上的一个格，格L的对偶格定义为

因此，从定理3得到下面推论.

推论1 假设：

(1) 概率测度μ是G上以Λ1⊂L*为谱的一个谱测度；

(2)A⊆L是有限离散集合，且(A，Λ2)是一个谱对.

则测度μ*δA是以Λ1⨁Λ2为谱的谱测度.