一个代数问题解法探究与推广

上海市七宝中学(201101) 李佳伟

上海师范大学(200235) 游佳乐

上海市浦东外国语学校东校(201206) 顾 锋

1.试题呈现

2.解法探讨

那么,除了纯代数的解法,还有没有其他方法呢?事实上,我们在上述解题过程中发现:这可以看作(2,1)点在直线上,而根据我们可以联想到直角三角形的周长.因此,题意可以转化为:一条直线经过(2,1)点(或者(1,2)点),与x轴正半轴、y轴正半轴相交,求围成的三角形周长的最小值.基于如上分析,这里再介绍一种比较巧妙的解法:

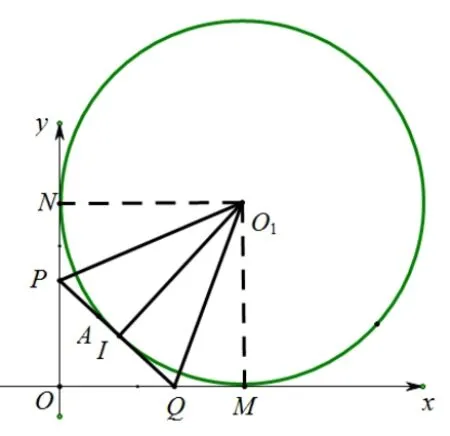
图1

解法二如图1:A(1,2),∆OPQ的斜边PQ过A点,P(0,p),Q(q,0),⊙O1为∆OPQ的旁切圆,与x轴相切于点M,与y轴相切于点N,与PQ相切于点I,O1点坐标为(r,r),易知∆OPQ的周长为且NP=PI,IQ=MQ,所以C∆OPQ=OM+ON=2r,而O1A≥r,所以(r−1)2+(r−2)2≥r2,解得r≥ 5或r≤ 1(舍),所以(C∆OPQ)min=2×5=10.

此外,我们还可以利用方程的思想解决这个问题:

当然,本题还有许多其他的解法,有兴趣的读者可以不妨尝试一下.

3.试题加强与推广

根据第二种利用几何意义的解法,笔者经过一番研究,解决了更为一般的问题.

问题推广1设直线PQ经过点A(a,b),a＞0,b＞0,与x轴,y轴分别交于Q,P两点,求∆OPQ周长的最小值.

我们不妨利用同样的方法尝试下:条件与解法二一致,因此,只有最后的不等式与解法二不同:(r−a)2+(r−b)2≥r2,因此r2−(2a+2b)r+a2+b2≥0,因此可得或者r≤a+因此我们可以看到,当a=1,b=2时,得到这与之前得到的结果是一致的.

若我们把条件中的a＞0,b＞0改成0,也就是说点A不一定在第一象限内,则可以利用对称性得到更为一般的结论:因此我们最终得到一个结论:若直线PQ经过点A(a,b)0,与x轴,y轴分别交于Q,P两点,则∆OPQ周长的最小值为

4.进一步推广

问题推广2设∠O＜180◦,点A(a,b)在∠O内,直线PQ过点A交∠O的两边于P、Q两点,求∆OPQ周长的最小值.

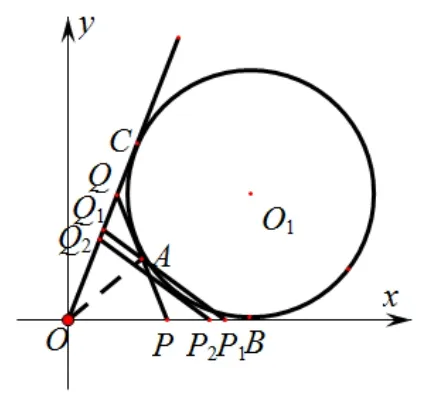
图2

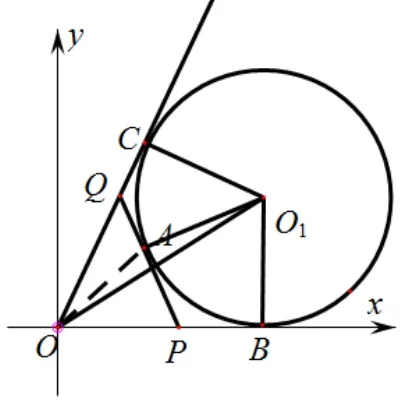
图3

我们可以采用与之前解法二类似的方法.如图2,圆O1与∠O的两边相切于B、C,且过点A,点A在劣弧上,当直线PQ与圆O1相切于点A时,∆OPQ的周长最小.事实上,过点A作圆O1的割线交∠O的两边于P1、Q1,在上存在一条平行于P1Q1的圆O1的切线交∠O的两边于于P2、Q2切点为D.所以∆POQ的周长

关于此类问题还可以从多个角度作进一步的探究,有兴趣的读者不妨尝试一下.

5.总结

数学题目千千万,要善于利用做过的题目,从中汲取有用的模型,有用的处理方法,有用的结论,建立题目之间的联想系统.新课标提出的数学核心素养中有数学建模和直观想象,建立哪些模型?想象哪些方法和结论?建立命题联想系统不失为一种好方法.

学生一直在解给定的题目,与解决问题相比,提出问题或许更为重要.在教学的过程中,我们要为学生提供微探究的机会,从给定的题目中提出新的问题,解决新的问题.在教学中不仅教会学生如何思考问题,还要帮助学生学会提出问题.