高考全国卷理科极坐标与参数方程的常见题型

重庆市南川道南中学(408400) 汪仁友

重庆市巴南区鱼洞南区学校(401320) 李加燕

在近几年的高考全国卷理科试题中,“极坐标与参数方程”是一道选做题,分值10分,但多数考生都选做该题.试题对知识的考查趋势基本稳定,既注重基础知识的考查,同时又突出对知识应用的考查,题型多集中在求曲线的(极坐标、参数、直角坐标)方程、极坐标与参数方程的应用.针对高考题的特点,复习备考时,应强化转化,突出应用,突破“用什么”(即究竟用“直”“极”还是用“参”),做好常规题.本文以近三年高考全国卷理科试题为例,解析高考极坐标与参数方程的常见题型.

一、求曲线的极坐标方程

例1(2019年高考全国卷Ⅱ)在极坐标系中,O为极点,点M(ρ0,θ0)(ρ0＞0)在曲线C:ρ=4sinθ上,直线l过点A(4,0)且与OM垂直,垂足为P.

(2)当M在C上运动且P在线段OM上时,求P点轨迹的极坐标方程.

评注求曲线的极坐标方程,通常采用两种方法:一是直接求出曲线的极坐标方程,二是先求曲线的直角坐标方程,再把直角坐标方程化为极坐标方程.

二、求曲线的参数方程

例2(2018年高考全国卷Ⅲ)在平面直角坐标系xOy中,⊙O的参数方程为(θ为参数),过点且倾斜角为α的直线l与⊙O交于A,B两点.

(1)求α的取值范围;

(2)求AB中点P的轨迹的参数方程.

评注求曲线的参数方程,关键是参数的选择,选择参数时,通常与题设有关.

三、求曲线的直角坐标方程

例3(2018年高考全国卷Ⅰ)在直角坐标系xOy中,曲线C1的方程为y=k|x|+2.以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ2+2ρcosθ−3=0.

(1)求C2的直角坐标方程;

(2)若C1与C2有且仅有三个公共点,求C1的方程.

解(1)由x=ρcosθ,y=ρsinθ得C2的直角坐标方程为(x+1)2+y2=4.

(2)由(1)知C2是圆心为A(−1,0),半径为2的圆.

由题设知,C1是过点B(0,2)且关于y轴对称的两条射线.记y轴右边的射线为l1,y轴左边的射线为l2.由于B在圆C2的外面,故C1与C2有且仅有三个公共点等价于l1与C2只有一个公共点且l2与C2有两个公共点,或l2与C2只有一个公共点且l1与C2有两个公共点.

当l1与C2只有一个公共点时,A到l1所在直线的距离为2,所以故或k=0.经检验,当k=0时,l1与C2没有公共点;当时,l与C只有12一个公共点,l2与C2有两个公共点.

当l2与C2只有一个公共点时,A到l2所在直线的距离为2,所以故k=0或经检验,当k=0时,l1与C2没有公共点;当时,l与C没有公22共点.

综上,所求C1的方程为

评注求曲线的直角坐标方程,通常是把极坐标的有关问题转化为直角坐标的问题,再利用解析几何的有关知识求出曲线的直角坐标方程.但也可以先求出曲线的极坐标方程或参数方程,再将其化为直角坐标方程(如本文例6(1)).

四、直线参数方程的应用

例4(2018年高考全国卷Ⅱ)在直角坐标系xOy中,曲线C的参数方程为(θ为参数),直线l的参数方程为(t为参数).

(1)求C和l的直角坐标方程;

(2)若曲线C截直线l所得线段的中点坐标为(1,2),求l的斜率.

解(1)曲线C的直角坐标方程为当cos0时,l的直角坐标方程为y=tanα·x+2−tanα,当cosα=0时,l的直角坐标方程为x=1.

(2)将l的参数方程代入C的直角坐标方程,整理得关于t的方程

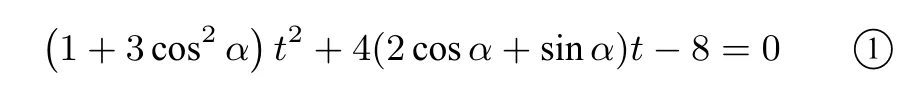
因为曲线C截直线l所得线段的中点(1,2)在C内,所以①有两个解,设为t1,t2,则t1+t2=0.又由①得

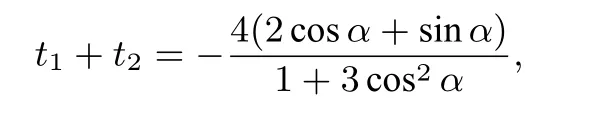
故2cosα+sinα=0,于是直线l的斜率k=tanα=−2.

评注处理直线与二次曲线有关中点、长度等问题时,利用直线的参数方程较为便捷,应充分利用参数t的几何意义,结合根与系数的关系求解.

五、圆、椭圆参数方程的应用

例5(2019年高考全国卷Ⅰ)在直角坐标系xOy中,曲线C的参数方程

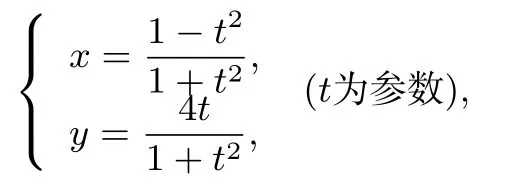
以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为

(1)求C和l的直角坐标方程;

(2)求C上的点到l距离的最小值.

解(1)C的直角坐标方程为l的直角坐标方程为:.(过程略)

(2)设C上点的坐标为:(cosθ,2sinθ),则C上的点到直线l的距离

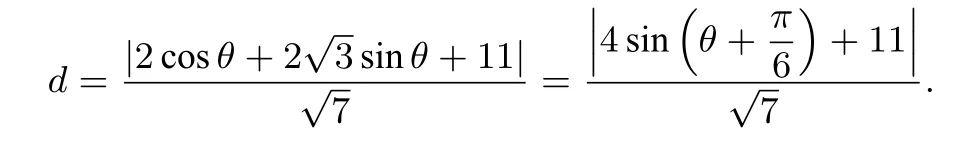
评注处理与圆、椭圆有关的最值、定值等问题,可以利用圆、椭圆的参数方程进行三角代换,将问题转化为用三角法求解.

六、极坐标方程的应用

例6(2017年高考全国卷Ⅱ)在直角坐标系xOy中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C1的极坐标方程为ρcosθ=4.

(1)M为曲线C1上的动点,点P在线段OM上,且满足|OM|·|OP|=16,求点P的轨迹C2的直角坐标方程;

(2)设点A的极坐标为点B在曲线C2上,求∆OAB面积的最大值.

解(1)设P的极坐标为(ρ,θ)(ρ＞0),M的极坐标为(ρ1,θ)(ρ1＞0).由题设知由|OM|·|OP|=16得C2的极坐标方程ρ=4cosθ(ρ＞0),因此C2的直角坐标方程为

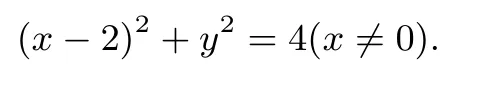
(2)设点B的极坐标为 (ρB,α)(ρB＞0).由题设知|OA|=2,ρB=4cosα,于是 ∆OAB面积

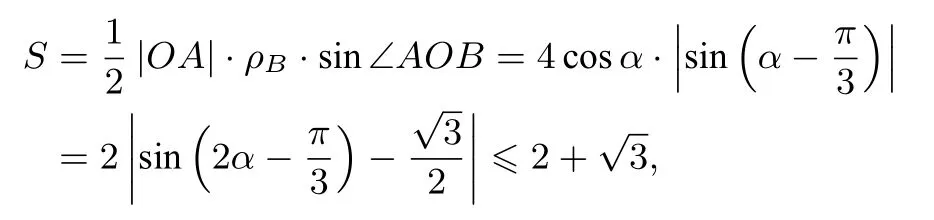
评注处理与长度、角度有关的问题,可以充分利用极径与极角的几何意义求解,常能简化运算.