一道2019年直线过定点模考题的探究与思考*

北京市第十二中学高中部(100071) 刘 刚

题目(2019年北京市海淀区一模文科第20题)已知椭圆的左顶点为A(−2,0),两个焦点与短轴一个顶点构成等腰直角三角形,过点P(1,0)且与x轴不重合的直线l与椭圆C交于M,N不同的两点.

(Ⅰ)求椭圆C的方程;

(Ⅱ)当AM与MN垂直时,求AM的长;

(Ⅲ)若过点P且平行于AM的直线交直线于点Q,求证:直线NQ恒过定点.

试题考查了椭圆的标准方程、几何性质、直线与椭圆的位置关系以及直线过定点问题,考查了设而不求、整体替换等数学方法,检验了运算求解、分析问题与解决问题的能力.试题解法多样,内涵丰富,为不同学生搭建了施展才能的舞台,是一道好题.第(Ⅰ)问求得椭圆C的方程为第(Ⅱ)问求得AM的长为下面重点探究第(Ⅲ)问的解法以及对试题的进一步思考.

1.解法探究

思路1设出M(x1,y1),N(x2,y2),然后表示出点Q的坐标,进而写出直线NQ的方程,接下来联立直线l与椭圆C的方程,运用韦达定理求解.

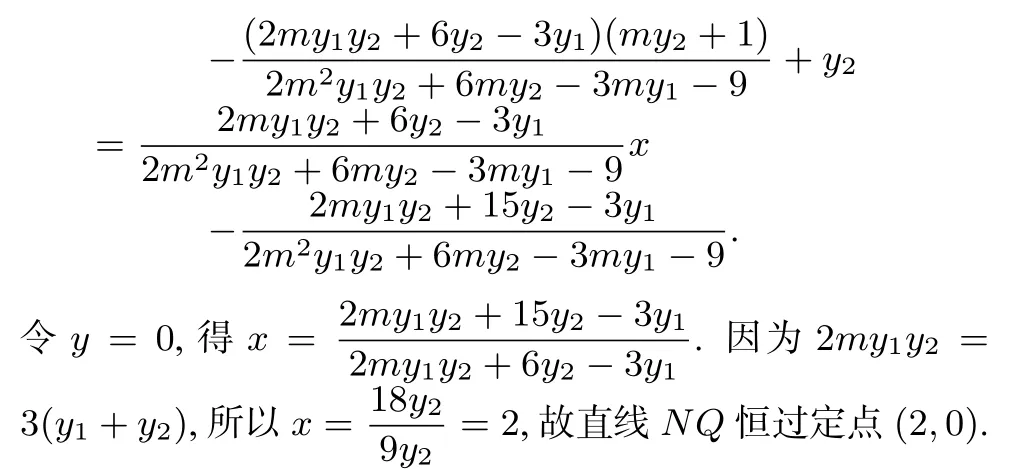
点评证法1由命题组提供,基本思路是借助直线NQ的方程以及韦达定理求解,但易想难算,对学生的运算能力要求较高.

思路2先考虑直线l与x轴垂直,求得直线NQ过点(2,0),由椭圆的对称性猜想直线NQ过定点(2,0),然后再转化为一般性的证明.

点评由于直线NQ所过的定点并没有给出,这给解答增添了难度,如果事先能知道这个定点,无疑给前进的道路指明了方向,将会柳暗花明.因此,在解决这种问题时,先通过特殊位置(如直线与坐标轴垂直、与曲线相切等)找出定点,再转化为一般性的证明,这是常用的解题思路.

思路3借助椭圆的参数方程求解.

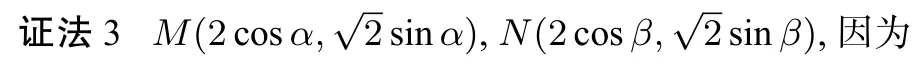
点评证法3借助椭圆的参数方程设出点M,N的坐标,然后借助三角公式进行推理,回避了韦达定理,令人耳目一新.

2 思考

思考1将试题一般化,有怎样的结论呢?经过探究,得到下面的性质.

性质1已知椭圆的左顶点为A,过点P(t,0)(0＜t＜a)且与x轴不重合的直线l与椭圆C交于M,N不同的两点.若过点P且平行于AM的直线交直线于点Q,则直线NQ恒过定点(a,0).

请读者参考以上三种证法,此处不再赘述.

思考2性质1是由推出了(iii)“直线NQ恒过定点(a,0)”,那么能否由(ii)(iii)推出(i)以及(i)(iii)推出(ii)呢?经过探究,结论依然成立,于是有下面的性质.

性质2已知椭圆的左、右顶点分别为为A,B,过点P(t,0)(0＜t＜a)且与x轴不重合的直线l与椭圆C交于M,N不同的两点.若直线NB与直线交于点Q,则PQ//AM.

性质4,6的证明留给读者自行完成.

以上从一道椭圆中的直线过定点问题出发,探究了其解法并将题目引申得到了几个优美性质.在解题教学中,教师要引导学生学会思考,积极探究,善于挖掘题目的背景,弄清试题的来龙去脉,养成良好的解题习惯,努力将题目的价值最大化,这样才会提高教学效率,从而提升学生的核心素养.

以下试题供读者练习

(1)若点P在椭圆C的内部,求直线AM的斜率的取值范围;

(2)设椭圆C的右焦点为F,点Q在y轴上,且∠PFQ=90◦,求证:AQ//BM.

(1)当n=0,且直线CD⊥x轴时,求四边形ACBD的面积;

(2)设n=1,直线CB与直线x=4相交于点M,求证:A,D,M三点共线.

3.(2008年全国高中数学联赛辽宁预赛)如图,已知椭圆的左顶点为A,右焦点为F(c,0),且 2b、a、c成等比数列.

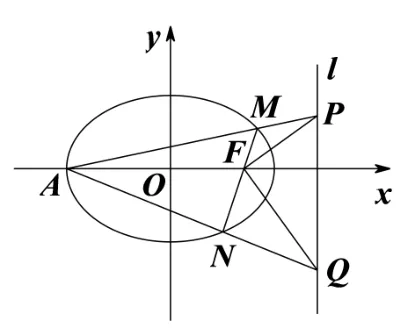
图

(1)求椭圆C的离心率;

(2)过点F的直线与椭圆C相交于M、N两点,直线AM、AN分别与右准线l相交于P、Q两点,求证为定值.