2019年高考全国Ⅱ卷理科第21题的解法探究与推广

广东省湛江一中培才学校(524037) 魏 欣

2019年高考全国卷理科第21题,题型结构常见,三个问题按梯度层层递进,难度步步提升,很好地考查考生的推理论证能力与运算求解能力,体现试题的区分功能与选拔功能.这就需要我们探究时仔细品味欣赏,进一步去揭示问题的本质特征,挖掘其潜在的价值和功能.本文对其进行多种解法解答与分析,通过与教材习题对比、与往年高考试题对比,力求找到命制此题的素材,希望通过加强对高考命题的研究,为师生复习备考指明方向,提高教学质量.

一、试题展示与评析

题目(2019年高考全国卷理科第21题)已知点A(−2,0),B(2,0),动点M(x,y)满足直线AM与BM的斜率乘积为记M的轨迹为曲线C.

(Ⅰ)求C的方程,并说明C是什么曲线?

(Ⅱ)过坐标原点的直线交C于P,Q两点,点P在第一象限,PE⊥x轴,垂足为E,连接QE并延长C交于点G.

(i)证明:∆PGQ是直角三角形;

(ii)求∆PGQ面积的最大值.

评析此题主要考查轨迹方程的求法,直线和椭圆的位置问题以及最值问题,意在考查学生的逻辑推理能力、运算求解能力,考查方程思想、数形结合思想、化归与转化思想,考查学生的逻辑推理、直观想象、数学运算等数学核心素养,检验了学生运算求解、分析问题、解决问题的能力.试题解法灵活,内涵丰富,综合性强,为不同学生搭建了施展才能的舞台,是一道有价值的试题.

二、解法探究

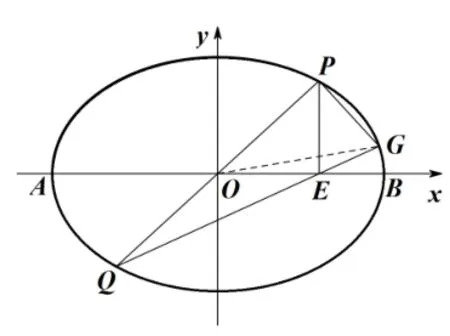
图1

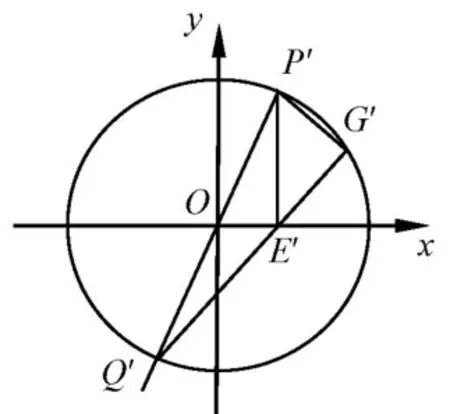
图2

图3

二、教材寻根

高考题的命题有些是来源于教材,但往往又高于教材,因而我们的课堂教学需要回归教材,扎根教材,根深才能叶茂,源远方能流长.2019年高考全国卷理科第21题第一问来源于新课标人教A版选修2-1第41页例3题.教材是命制高考试题的一个源头,这也符合“源于教材,高于教材”的命题理念,这就要求我们了解高考试题的来龙去脉,领悟教材和高考试题的功能,这对跳出题海,正确把握高考复习方向,有着重要的意义和作用.

题目(新课标人教A版选修2-1第41页例3)设点A,B的坐标分别为(−5,0),(5,0),直线AM,BM相交于点M,且它们的斜率之积是求M点的轨迹方程.

教材中的例题和习题具有典型性与代表性,能有效检查学生对重点知识的掌握及灵活应用的程度.分析历年的高考试题,可以发现,很多高考试题的原型都来自于课本教材,适当地进行一些改编和创新.高考的命题指导思想中也指出,要考查学生对基础知识、基本能力的掌握程度和运用所学知识分析、解决问题的能力.因此,对教材例、习题的探究是高三备考复习的重要方式之一.

三、性质研究

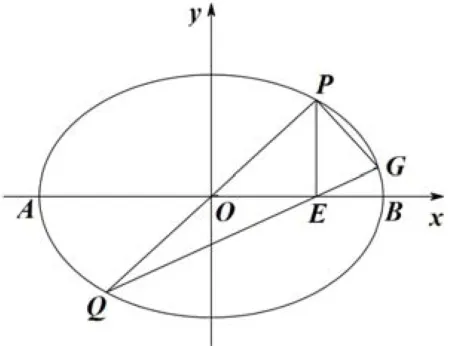
图4

结论二如图4所示,已知椭圆过坐标原点的直线交曲线C于P,Q两点,设P在第一象限,过P作x轴或y轴的垂线,垂足为E,连接QE交曲线C于点G.则有

四、真题回顾

由以上结论不难发现,历年高考题也均考查以上圆锥曲线的定值和最值问题,体现了高考试题“常考常新,推陈出新”的理念,在解决相关问题时,灵活运用上面的性质,不仅比较容易找到解题的突破口,而且往往会获得简洁、明快的解题方法和途径.下面略举几例说明上述结论的应用.

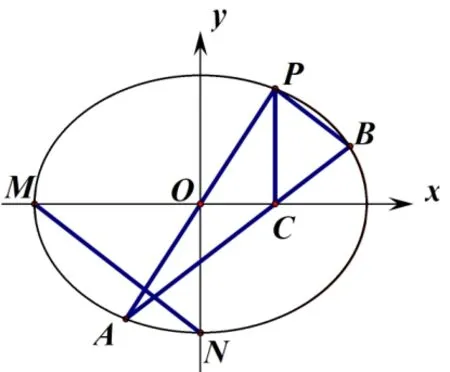
图5

例1(2011年高考江苏卷第18题)如图5,在平面直角坐标系xOy中,M,N分别是椭圆的顶点,过坐标原点的直线交椭圆于P,A两点,其中P在第一象限,过P作x轴的垂线,垂足为C,连接AC,并延长交椭圆于点B,设直线PA的斜率为k.

(Ⅰ)当直线PA平分线段MN时,求k的值;

(Ⅱ)当k=2时,求点P到直线AB的距离;

(Ⅲ)对任意k＞0,求证:PA⊥PB.

点评例1与2019年高考全国Ⅱ卷理科第21题的已知条件非常相似,区别在:例1中曲线方程直接给出,而全国Ⅱ卷的试题则把曲线方程设置为第(Ⅰ)问进行求解,两道试题考查的难点都是”垂直”问题.此外,例1的第(Ⅰ)问和第(Ⅱ)问设置比较基本,面对大部分考生,难度比全国Ⅱ卷试题低;全国Ⅱ卷试题第(Ⅰ)问利用斜率定义求解曲线方程,属于概念题型,大部分考生能够完成,但从第(Ⅱ)问题开始难度提高.整体上看,两道试题考查的目标与解题思路一致,都是考查曲线轨迹知识与解析几何相关知识,考查考生数学阅读水平,数形结合思想、推理论证能力和运算求解能力.

例2(2012年高考湖北卷理科第21题)设A是单位圆x2+y2=1上的任意一点,l是过点A与x轴垂直的直线,D是直线l与x轴的交点,点M在直线l上,且满足|DM|=m|DA|(m＞0且1).当点A在圆上运动时,记点M的轨迹为曲线C.

(Ⅰ)求曲线C的方程,判断曲线C为何种圆锥曲线,并求其焦点坐标;

(Ⅱ)过原点且斜率为k的直线交C于P、Q两点,其中点P在第一象限,它在y轴上的射影为N,直线QN交曲线C于另一点H.是否存在m,使对任意的k＞0,都有PQ⊥PH?若存在,求m的值;若不存在,请说明理由.

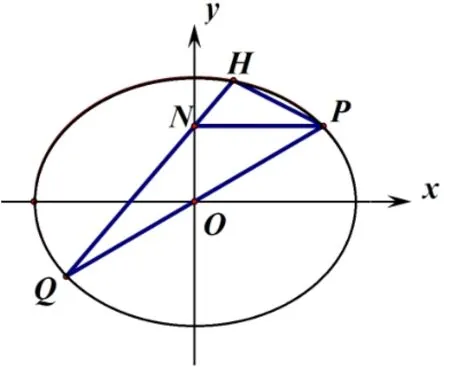
图6

点评例2引入参数m,讨论轨迹方程,考查椭圆的定义与几何性质知识,考查考生分类讨论思想和运算求解能力.如图6,第(Ⅱ)问在第(Ⅰ)问的基础上,探究PQ⊥PH成立所需的m值,虽然已知条件把x轴换成y轴,但是解题思路与全国Ⅱ卷和江苏卷试题一脉相承,解题方法殊途同归.考查直线与椭圆位置关系的相关知识,考查考生数形结合思想、推理论证能力和运算求解能力,同时例2与全国Ⅱ卷第21题在试卷中的定位类似,都是作为压轴题,体现试题的区分功能与选拔功能.

五、备考建议

G·波利亚有句名言:“掌握数学就是意味着善于解题,如果我们在日常的教学中,能对课本例习题作深入的研究,一题多解,一题多变,多题一法进行变式教学,立根课本,必定能取得丰硕的成果”.

在数学教学中,我们要善于挖掘教材的潜在教学功能.教材中有一些典型性题目,它们或者是重要的结论,或者体现某种数学思想方法,或者是某个一般数学命题的具体形式,它的延伸、转化和拓广,可以呈现出丰富多彩的数学内容.我们必须充分重视课本典型例题、习题的探究,这是”用教材教”之根本,也是教师专业成长的必有之路.

随着新一轮高中课程改革的实施,教师对解析几何的教学应由传统的“结果性教学”转变为素养立意的“过程性教学”,这就要求教师在教学过程中,不仅要让学生知其然,更要知其所以然,同时引导学生了解甚至主动去探究解析几何问题的本“源”,学会举一反三,而不是就题解题,机械模仿.一方面,教师探寻解析几何问题的本“源”,追溯数学思维发展的源泉,可以提升教师自身数学专业素养和专业化水平;另一方面,教师把握解析几何问题的“流”[4],可以培养学生多维度思考问题的习惯,登高望远,拓展视野,如全国Ⅱ卷的第(Ⅱ)问,能够培养学生思维的深度和广度,提高学习数学的兴趣,挖掘数学学习的潜能.