稀薄燃烧发动机改型设计及正时策略优化*

杨 靖，罗贤芳，何联格，陶文祝，赵 超

（1.重庆理工大学车辆工程学院，重庆 400054； 2.重庆理工大学，汽车零部件先进制造技术教育部重点实验室，重庆 400054）

前言

目前，能源危机问题受到各界的广泛关注，人们对发动机提出了更高要求。因此降低汽油机的燃油消耗率成为研究的重点与热点，稀薄燃烧发动机应运而生。由于稀薄燃烧发动机的过量空气系数较大、对燃烧过程要求高等特点［1］，因此需要分析设计计算与之匹配的配气正时策略和点火正时策略。

本文中以某高速汽油机改型的稀薄燃烧发动机为研究对象，采用响应面法对改型后稀薄燃烧发动机的配气正时和点火正时进行优化计算，以进排气凸轮正时、过量空气系数和点火正时为设计变量，以提高有效功率和降低有效燃油消耗率为优化目标，建立了利用响应面法优化发动机正时的计算流程，改善了发动机的燃油经济性；同时将响应面应用于发动机优化中，提高了仿真优化的效率，为响应面在发动机优化上的应用提供了思路。

1 性能仿真模型建立与标定

1.1 发动机工作过程仿真模型建立

GT-POWER以一维CFD为基础，采用有限容积法对热流体进行计算。对发动机内流体状态进行计算的控制方程为

连续方程：

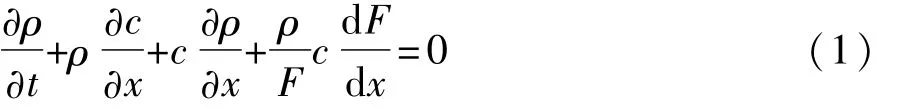
动量方程：

能量方程：

式中：ρ为气体密度；c为气体流速；F为管道截面积；f为管壁摩擦阻力。

本文中以某进气道喷射的高速汽油机为研究对象，将其改型为稀薄燃烧发动机，依据原机的三维模型和台架实测边界条件建立仿真计算模型，见图1。考虑混合气运动、燃料特性和便于控制点火正时，缸内燃烧模型选用 EngCylCombSITurb模型［2］。表1为原机主要技术参数。

图1 原机性能仿真模型

1.2 性能仿真模型标定

由于该发动机为摩托车用单缸高速汽油机，较车用发动机的转速高，额定功率点转速为8 000 r／min。为验证该仿真模型的准确性和可靠性，对原机额定功率点转速8 000 r／min的模拟计算与试验中实测的缸内压力曲线和瞬时放热率曲线进行对比分析。图2为原机在8 000 r／min时的缸内压力曲线和瞬时放热率曲线模拟值和实测值。

表1 原机主要技术参数

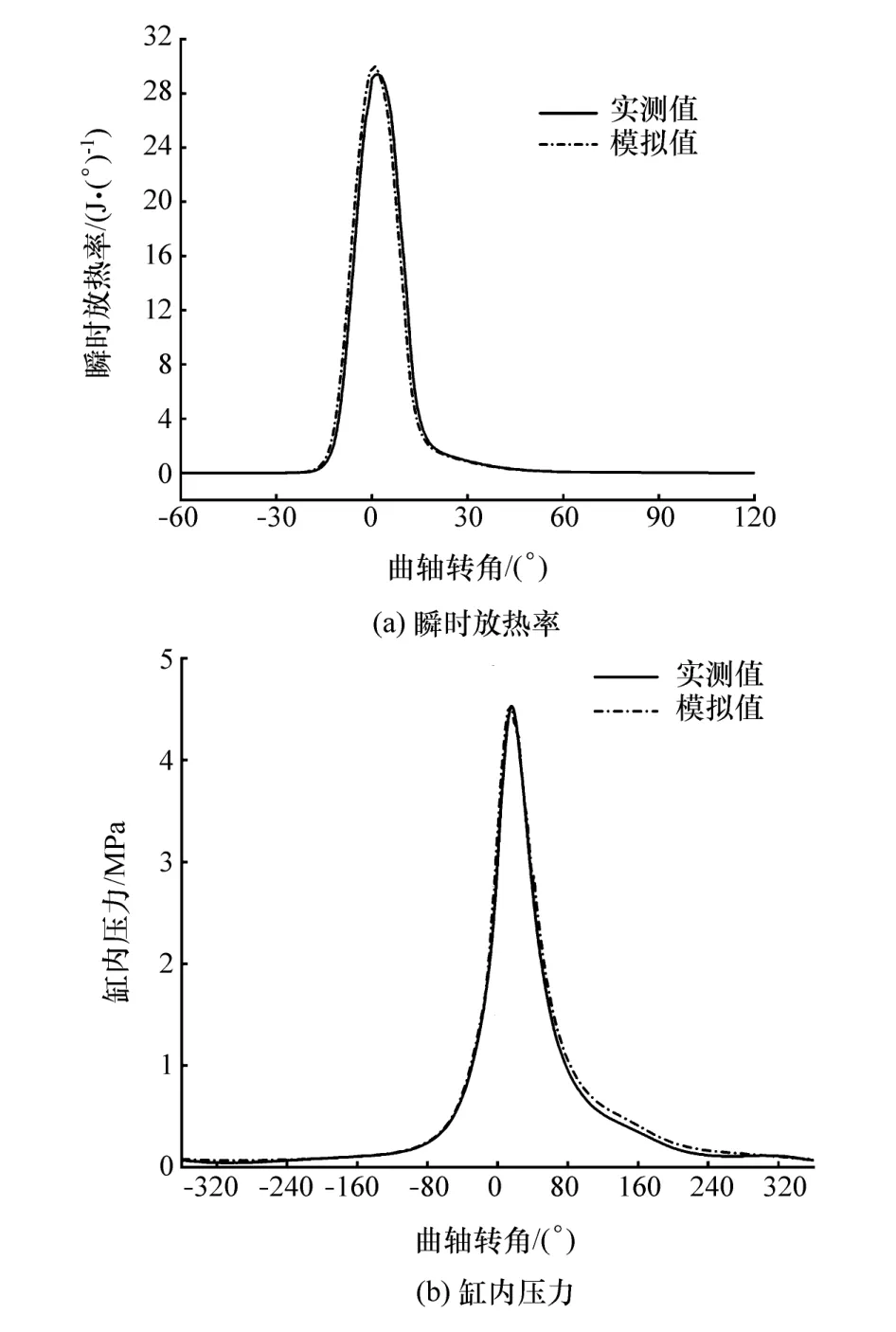
图2 模型验证对比图

从图2（a）瞬时放热率图中可知，最大瞬时放热率试验值较仿真计算值稍低，这是由于在计算瞬时放热流程时做了一定的基本假设及简化，但整体瞬时放热率趋势变化符合工程误差要求。从图2（b）缸内压力的模拟值与实测值对比可以看出，通过对仿真模型标定后，当转速为8 000 r／min时模拟值与试验值的缸内压力的变化趋势一致，最大误差率小于5%，模型精度较高，满足工程要求，可利用该模型进行参数分析与优化。

2 稀薄燃烧发动机的改型设计

在均质混合燃烧的进气道喷射的汽油机稳定燃烧界限空燃比可达到17左右［3］。为实现稀薄燃烧，对原机进行了主要结构和关键参数改型设计。主要包括燃烧室结构改型、燃油喷射改进和凸轮型线设计。

2.1 燃烧室改进设计

为采用较稀的混合气实现稀薄燃烧，提高循环热效率，对原机的燃烧室进行了较大改动。如图3所示，将半球形燃烧室改为浴盆形燃烧室，使燃烧室结构更紧凑，实现了压缩比从9.5提高到10.3。并在燃烧室的链条侧增设一副火花塞，实现由单火花塞点火向主副双火花塞点火的转变，减少散热损失，使得燃烧迅速，进一步缩短燃烧持续期。

图3 改进前后燃烧室

2.2 燃油喷射改进设计

喷油器的安装角度与位置以及喷油器的类型在喷雾和混合气制备过程中起着十分重要的作用［3］。因此，应合理选择喷油器的位置、角度和喷嘴类型。

原机喷油器安装在节气门后约2 cm的位置，喷油器安装位置离气缸较远，使缸内混合气的变化滞后于燃油喷射的控制，从而导致过量空气系数响应较慢且波动较大［4］。鉴于此，改型机将喷油器的安装位置调整为进气道进口处，角度调整为开阀喷射，减小喷雾着壁。同时，将喷油器类型由0.61 mm、2孔喷咀换为0.18 mm、6孔喷咀喷油器，使雾化效果更好，燃油蒸发速度加快，过量空气系数响应加快。图4为改型前后喷油器喷油特性试验比较。

图4 不同喷雾特性比较

2.3 凸轮型线改进设计

在保证气门与活塞不发生干涉的前提下，将进排气门升程分别提高到7.8和7.6 mm，并重新对缓冲段进行了合理设计。图5为改型前后气门升程对比，在确保配气机构运动学与动力学合理的前提下，气门重叠角适当减小，降低了进气倒流，且改型后气门最大升程增大，显著提高了发动机充气效率。

图5 改型前后气门升程曲线

3 基于响应面法的正时策略优化

将原机改型为稀薄燃烧发动机后，需要对稀薄燃烧发动机进行重新标定，为更好地优化改型后发动机，同时为台架试验标定提供指导，节省标定时间，故采用基于响应面法对进排气正时、空燃比和点火正时进行优化。

3.1 响应面法

响应曲面是数学方法和统计方法的产物，将系统的响应作为一个或多个因素的函数，运用图形技术将这种函数关系显示出来，借助图形选择试验设计中的最优化条件［5］。

响应函数可用模型表示为

式中：y为响应输出；xi为响应因子；ε为响应的观测误差［5］。假定ε在不同的实验中是相互独立的，均值为0，方差为 σ2。

当试验区域远离曲面的最优位置时，可采用自变量某区域内的1阶模型来逼近。

式中βi为xi的斜率或线性效应。

在输入变量的水平接近响应曲面的最优区域或位于最优区域中，为更精确逼近并识别出最优输入变量的最优水平组合，采用2阶模型来逼近［5］。

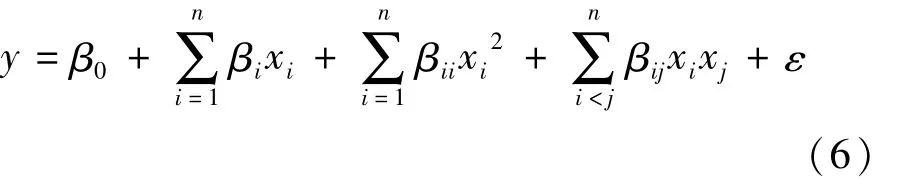
式中：βi为xi的线性效应；βii为编码xi的2阶效应；βij为编码xi和xj的交互作用效应。

由试验设计方法得到初始设计点，利用真实求解器求解初始设计点的响应输出，对得到的响应输出进行统计分析，建立设计变量与目标响应输出的响应曲面［6－7］。从而对建立的响应曲面进行评估，在精度水平满足要求的前提下，利用优化算法在响应曲面上（即使用虚拟求解器）搜寻最优设计变量的解，然后在仿真模型中验证选取的最优设计变量，最后利用试验验证最优设计变量。由于利用响应曲面优化设计使用的是RSM函数而不是真实求解器进行计算，因此响应面优化比常规优化更快，效率更高。

3.2 试验设计变量和响应

以进气凸轮正时、排气凸轮正时、过量空气系数和点火正时为设计变量，以有效功率（BKW）和有效燃油消耗率（BSFC）为响应输出。优化模型中边界与约束条件见表2。在模型进行计算时将进排气提前角转化为进排气凸轮正时，进排气凸轮正时分别是指压缩上止点到进排气门开启到最大升程对应的曲轴转角。图6为建立基于响应面法的正时参数优化模型。

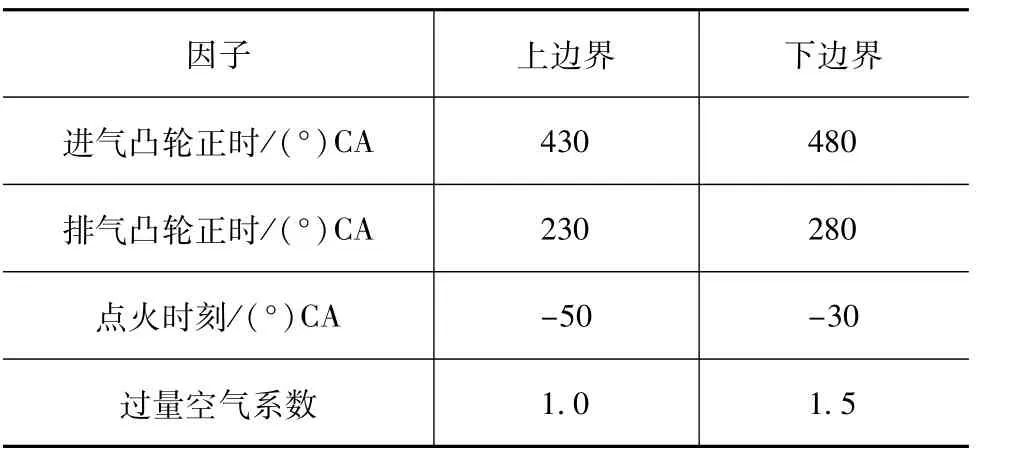
表2 优化模型边界及约束条件的设置

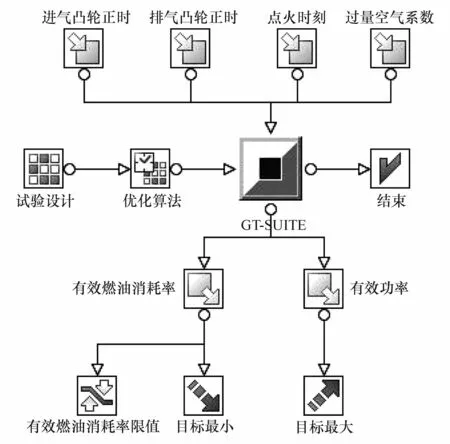
图6 基于响应面优化仿真模型

3.3 响应面的建立与验证

试验设计中初始数据点分布与响应曲面的精度密切相关，训练点越多，响应面越可靠［8］。本文中采用均匀拉丁超立方（ULH）选取初始数据。ULH是一种先进的蒙特卡罗采样，采用最小化输入变量之间的相关性，并使生成的设计之间的距离最大化［9］。初始点在可变范围内相对均匀分布，能表现出全部试验空间的特征。采用2阶响应曲面，试验设计的初始数据点应满足识别计算2阶多项式响应表面所需的最小训练点的两倍或至少大于最小值［7，10］，因此实际初始设计试验的个数确定为50个。

基于试验设计的计算结果，采用RBF（径向基函数）、KR（克里金插值法）和NN（人工神经网络）3种回归分析方法进行响应曲面拟合，表3和表4为3种回归分析方法建立的响应面模型精度评估数据。

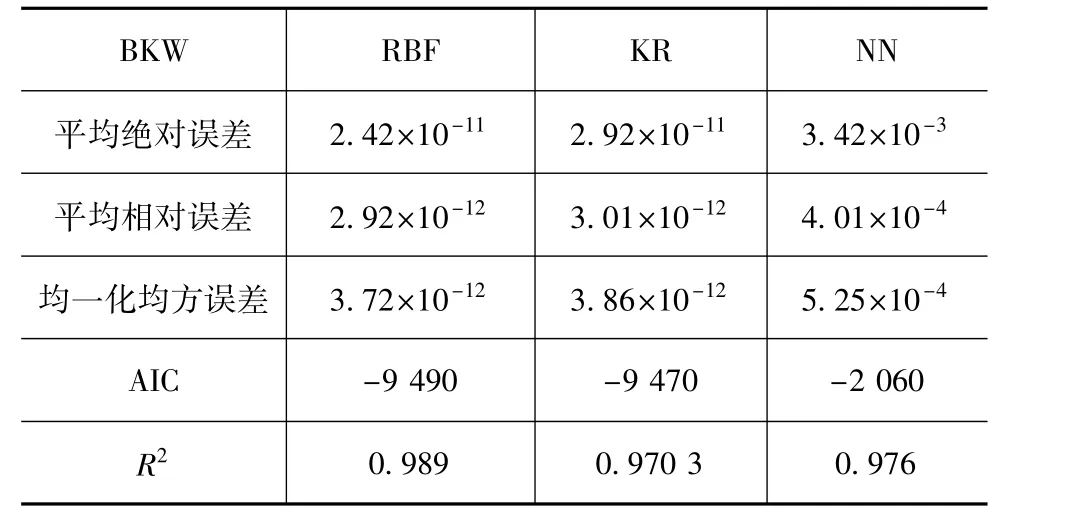
表3 不同回归分析方法构建的有效功率响应面模型误差值

表4 不同回归分析方法构建的有效燃油消耗率响应面模型误差值

由表3和表4可知，RBF回归拟合的平均相对误差、平均绝对误差、均一化均方误差和AIC均低于KR和NN，RBF回归拟合的判定系数R2最接近1，即RBF函数拟合精度最高，因此，选用RBF拟合响应面模型。

图7和图8为采用RBF函数拟合8 000 r／min全负荷时的响应曲面。

图7 进气与排气凸轮正时对有效功率的影响模型

图8 点火时刻与过量空气系数对有效功率的影响模型

3.4 基于响应面正时参数优化

利用建立的响应曲面进行虚拟优化，优化算法采用带精英策略的非支配排序的遗传算法（NSGAII），降低算法的计算复杂度，利用拥挤度和拥挤度比较算子使准帕累托域中的个体能扩展到整个帕累托域［11］。

优化目标函数为

式中：αIN、αEX、αST、αλ分别为进气门凸轮正时、排气门凸轮正时、点火正时、过量空气系数的目标函数。

初始种群为试验设计的50个初始数据点，种群代数为100，在5 000个数据点中寻优，得到响应输出的Pareto解。

由图9可见，优化目标帕累托前沿清晰可见，所有最优解都是平等的。考虑到设计变量的变化范围，虚拟设计非常接近真正的帕累托前沿。由于评估所有最优解的计算庞大，只选择了帕累托前沿上3组设计使用真实求解器进行验证，见表5。表6和表7为虚拟求解器与真实求解计算值的相对误差分析。

图9 优化目标的帕累托前沿

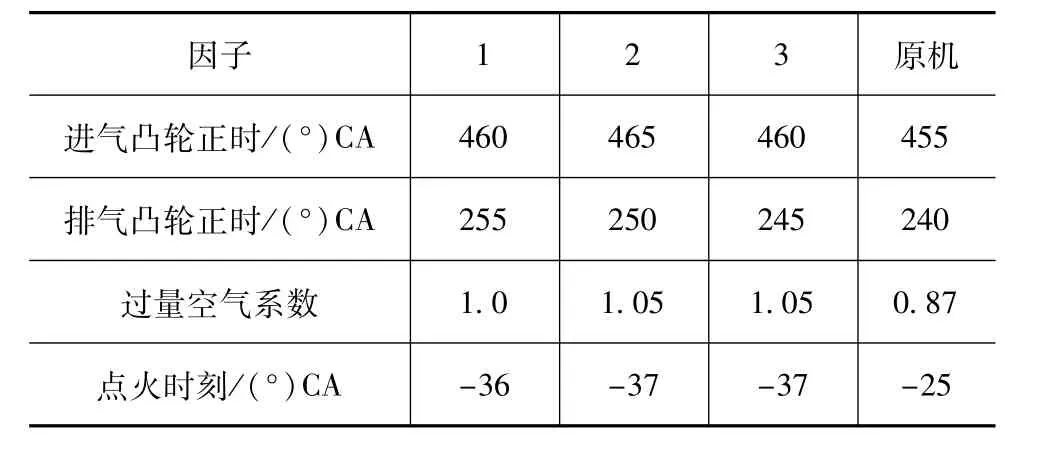
表5 响应面模型优化后参数值与目标函数值

由表6和表7可知，利用响应面模型虚拟求解与真实求解器计算的有效功率相对误差小于2%，有效燃油消耗率相对误差小于0.5%，利用响应面模型虚拟求解的结果有效，可利用响应面模型代替真实求解器计算，节约优化计算时间。

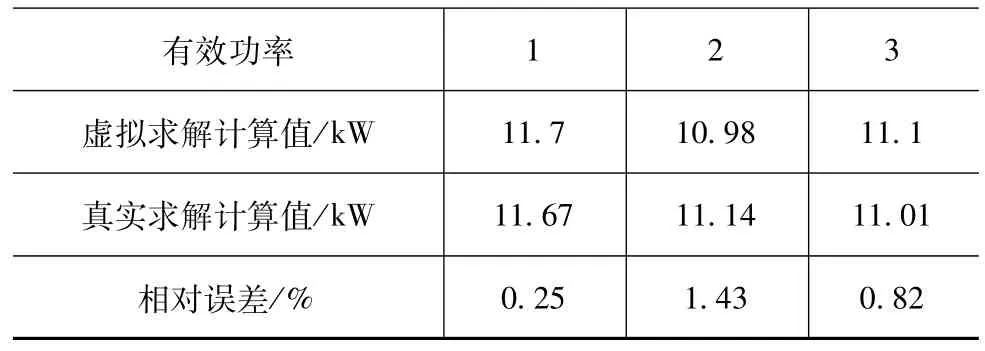
表6 虚拟求解器与真实求解器计算有效功率误差

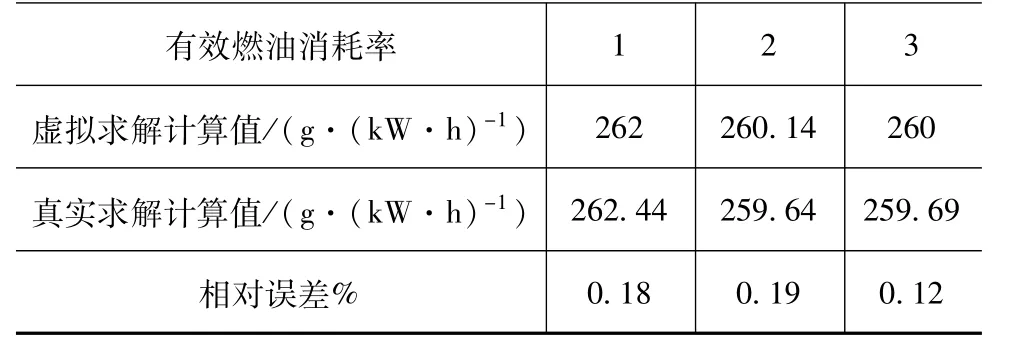
表7 虚拟求解器与真实求解器计算有效燃油消耗率误差

由于该发动机没有VVT，根据实际使用要求，在各转速帕累托前沿中侧重高转速工况，确定进气提前角为56°CA，排气提前角为72°CA，即减小上止点前气门重叠角，有效避免废气倒流。表8为设计变量与响应输出值。

4 性能预测与试验验证

基于原机性能模型，对改型后稀薄燃烧发动机进行预测。为验证基于响应面法的仿真优化模型的准确性和精度，同时确保优化计算结果对台架试验的有效指导性，以优化后正时策略为指导，对改型后发动机进行台架试验。

由图10可知，优化后试验值与性能预测值变化趋势一致，最大误差为1.4%。通过对原机改型，各转速下发动机有效功率都有提升，其中高速时有效功率提升更为明显，这是由于在优化正时策略时侧重考虑到高速性能。优化前后最大有效功率提升9.7%；其中正时策略优化可将最大功率提升3.37%。

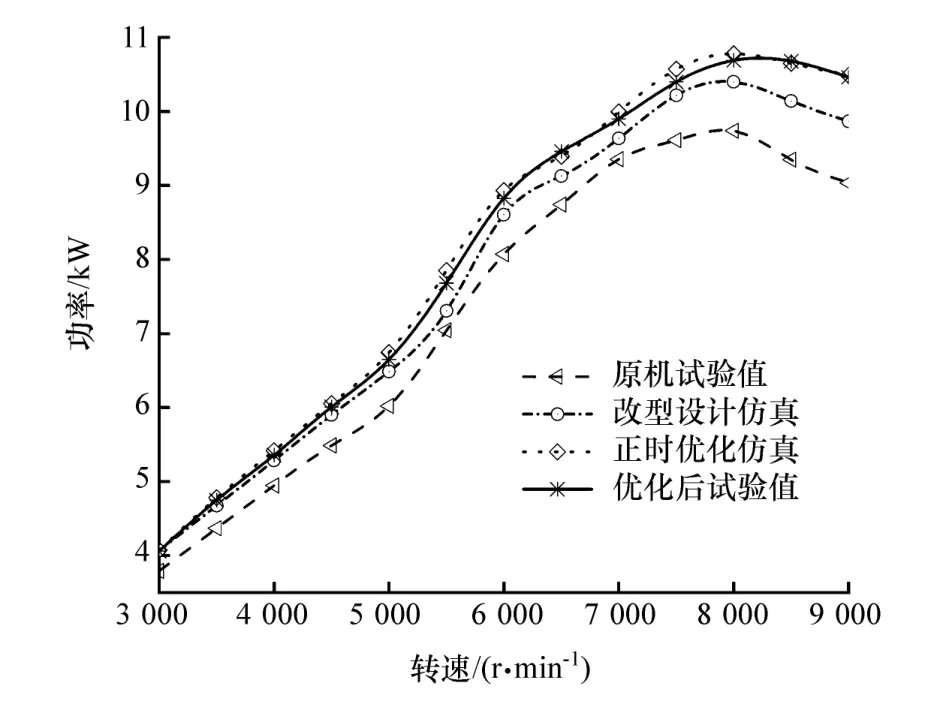
图10 优化前后功率对比与验证

由图11可知，优化后最低有效燃油消耗率试验值与模型预测值的最大误差为1.08%，最低燃油消耗率提升3.9%，优化正时策略提升1.5%。

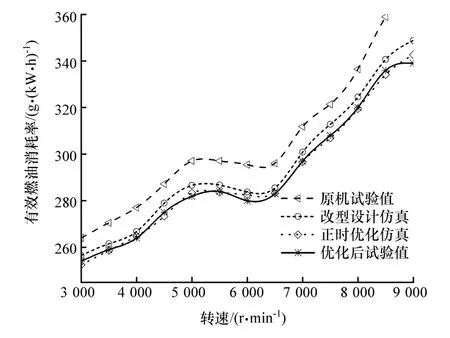
图11 优化前后燃油消耗率对比与验证

5 结论

（1）较标准混合比燃烧时，优化后稀薄燃烧发动机的进排气提前角都减小，其中进气提前角减小10°CA，排气提前角减小12°CA。

（2）利用响应面近似模型优化发动机配气与点火正时的方法是有效的，合理设计试验，利用合理的统计分析方法建立响应面模型，可使虚拟求解器与真实求解器的计算误差在允许范围内，计算结果可为标定试验提供参考。

（3）采用基于响应面法的优化方法，利用响应面虚拟优化可大大节约优化时间优化成本。

（4）优化后稀薄燃烧发动机最低有效燃油消耗率可降低3.9%，最大有效功率可提升9.7%。