镁铝合金车轮胶栓复合连接稳健性优化设计*

王登峰，许文超

（吉林大学，汽车仿真与控制国家重点实验室，长春 130022）

前言

轻质合金车轮的应用提高了汽车行驶的稳定性和安全性［1］。本文中提出镁铝合金组装式车轮的设计方案，该组装式车轮在强度、刚度和冲击强度等方面表现出优良的性能［2］，但在动态弯曲疲劳寿命试验中，连接轮辐和轮辋的螺栓在循环加载6.5万次后断裂，轮辋与轮辐间的连接可靠性需要提升。

螺栓连接在异种材料的连接中应用最为普遍，已有诸多学者对影响螺栓连接结构疲劳强度的因素进行了研究。Esmaeili等［3］的研究结果表明，螺栓预紧力能够提高接头的疲劳寿命。Esmaeili-Goldarag等［4］在进一步研究中指出，栓接接头的预紧力会随载荷环境的变化而产生相应变化。Abazadeh等［5－6］分别研究了螺栓干涉配合和循环载荷范围对铝合金双搭接螺栓连接结构的疲劳寿命的影响。在螺栓连接的基础上提出胶栓复合连接方式，Hoang-Ngoc等［7］建立了基于柔性胶的胶螺复合连接仿真模型，通过数值分析得出：胶螺复合连接接头的疲劳寿命高于螺栓连接接头的疲劳寿命，在胶栓复合连接结构中，胶层的厚度［8］、胶层的种类［9］、胶层与被连接板间的粘附程度和被连接板的表面处理方式［10］等因素均对接头的疲劳强度有重要影响。在胶栓接头中，胶层和螺栓所承担的载荷传递比会影响接头的应力分布，进而影响到其疲劳强度［11－13］。当胶栓接头处于复杂多变的载荷环境时，胶层和螺栓的载荷传递比将时刻发生变化，接头的载荷形式难以有效预测。针对不同的载荷环境，如何匹配性设计螺栓、胶层的结构和力学参数，进而提高接头的疲劳强度，是有待解决的技术难题。与此同时，在实际工程中，车轮结构尺寸参数与胶栓连接工艺带来的不确定因素会导致车轮胶栓连接的性能产生较大波动，如何有效提升车轮胶栓连接可靠性的问题有待进一步解决。

现有研究中胶栓接头连接性能的研究大多以单搭接或双搭接接头为研究对象，将胶栓复合连接应用到汽车结构件上；综合考虑连接螺栓、结构胶的结构和力学参数对结构件性能的影响，通过匹配性设计实现连接结构最优整体性能的研究较为匮乏。组装式车轮受到来自路面的载荷激励，其胶栓接头处于复杂多变的服役环境，连接的失效模式难以直接预测，故本文中在前人的研究基础上，以镁铝合金组装式车轮连接螺栓的疲劳强度和结构胶的断裂失效为主要研究目标，借助多目标优化设计理论和方法，寻优得到车轮胶栓复合连接的最佳结构和工艺参数，并采用6σ稳健性设计理论提高胶栓连接的可靠性。

1 建模与验证

组装式车轮通过沿车轮中心周向分布的20个M6圆柱头内六角螺钉连接，螺钉材料选取SUS304钢或45号钢，轮辐材料为6061铝合金，轮辋材料为ZK61M镁合金。组装式车轮螺栓连接有限元模型如图1（a）所示，螺栓和轮辋采用六面体单元划分，如图1（b）和1（c）所示，轮辐采用四面体单元划分，如图1（d）所示，共得到车轮模型的单元总数为1 294 034，节点总数为849 379。依据汽车用螺纹紧固件紧固扭矩标准（QC／T 518—2007），在车轮有限元模型中，将20个连接螺栓的预紧力值均设为7 900 N·m，为更真实地模拟螺栓的连接状态，将螺母与轮辋间建立摩擦因数为0.2的*Automatic＿surface＿to＿surface接触、螺帽与轮辐间建立摩擦因数为0.2的*Automatic＿surface＿to＿surface接触、轮辐与轮辋间建立摩擦因数为0.05的*Automatic＿surface＿to＿surface接触。

图1 组装式车轮栓接有限元模型

参照GB／T 5334—2005《乘用车车轮性能要求和试验方法》和相关文献［14］，建立组装式车轮弯曲静力仿真模型，将仿真结果导入MSC.Fatigue疲劳分析软件，并载入车轮材料的试验S-N曲线和弯曲疲劳试验载荷［2］，螺栓材料的S-N曲线根据其抗拉强度在疲劳软件中估算得到；基于Palmgren-Miner线性疲劳损伤累计理论，描述见式（1），使用名义应力法［15］（S-N法）对车轮进行疲劳寿命预测，求解时根据Von Mises准则，存活率选取50%（常规的疲劳台架试验存活率一般为50%［16］）；将仿真得到的车轮疲劳损伤与弯曲疲劳台架试验结果对比，如图2所示，将仿真得到的SUS304材料和45号钢材料螺栓的疲劳损伤与弯曲疲劳试验结果对比，如图3所示。

式中：m为载荷幅值的应力水平级数；ni为第i级载荷循环次数；Ni为第i级载荷下的疲劳寿命；D为结构的总损伤。Miner准则认为损伤之和达到1时，结构发生疲劳破坏。

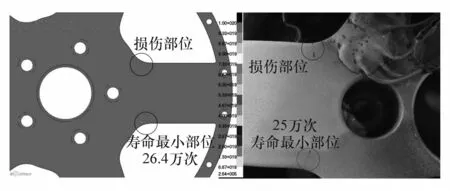
图2 轮辐疲劳寿命仿真云图与试验损伤

图3 螺栓疲劳寿命仿真云图与试验损伤

从图2和图3可以看出，仿真和试验得到的轮辐的最小疲劳寿命分别为26.4和25.0万次，两者相对误差为5.6%，损伤位置均位于辐条根部圆弧处。两种材料螺栓仿真得到的最小疲劳寿命分别为6.14和8.96万次，和试验的相对误差均在6%以内，损伤位置均位于靠近螺头的螺杆表面。

2 结构胶本构模型

结构胶模拟常采用双线性弹塑性模型［17］、CZM模型［18］和 Gurson模型［19］，文中将弹塑性模型作为胶层的本构模型。采用最大应力准则来判断胶层的失效，如式（2）和式（3）所示。

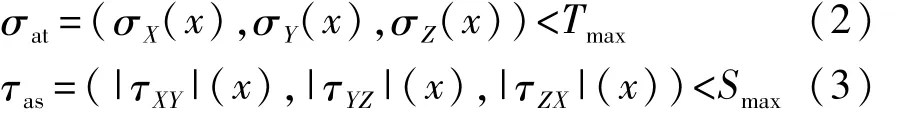
式中：σX、σY、σZ分别表示胶层在空间坐标系 X、Y、Z方向的最大拉伸应力，MPa；Tmax为胶层的拉伸强度，MPa；｜τXY｜、｜τYZ｜、｜τZX｜分别为胶层在 X、Y、Z方向的最大剪切应力，MPa；Smax为胶层的剪切强度，MPa；σat（x）为三向最大拉伸应力的集合，MPa；τas（x）为三向最大剪切应力的集合，MPa。

选取结构胶环氧树脂胶A、丙烯酸脂胶B与C和环氧树脂胶D，依据GB／T 1040.1—2006标准，将胶条加工成标准的哑铃型试样，对其进行准静态拉伸，得到结构胶的应力应变曲线，如图4所示。依据GB 7124—2008标准，设计铝镁合金单搭接胶粘接头，得到不同种类结构胶的剪切强度，如图5所示。

图4 胶条应力应变曲线

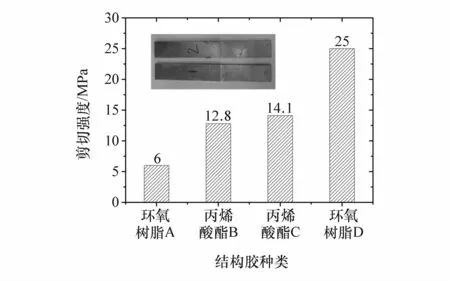
图5 不同种类结构胶的试验剪切强度

3 胶栓连接稳健性优化模型

建立组装式车轮胶栓复合连接有限元模型，图6为胶层、单个螺栓和车轮的连接关系，胶层采用实体单元模拟，初始厚度0.2 mm，使用六面体单元进行网格划分，胶层本构模型为双线性弹塑性材料模型，胶层与轮辐、轮辋的接触面分别建立绑定接触。螺栓连接的参数设置和前文相同。

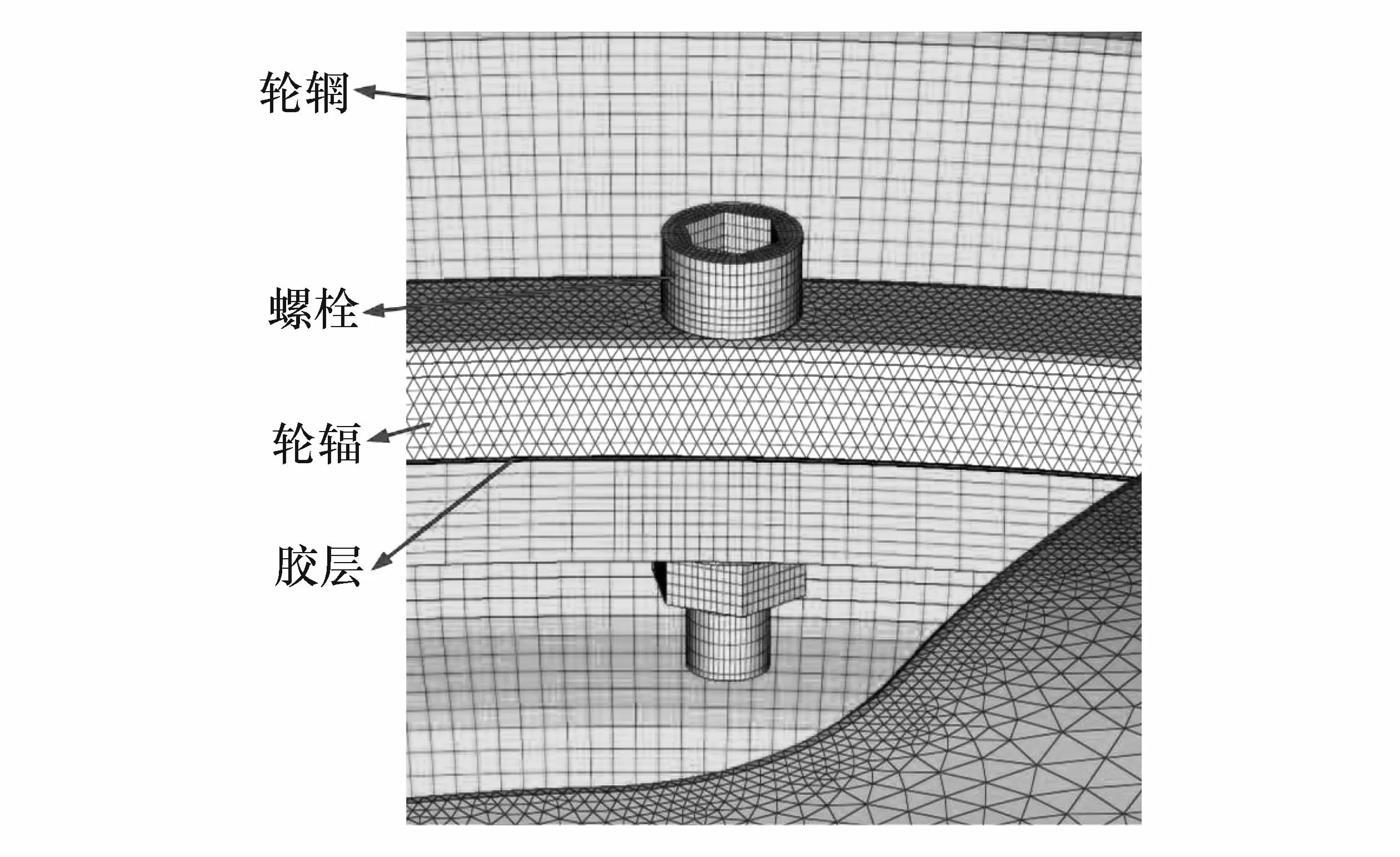
图6 胶层、螺栓和车轮的连接关系

3.1 设计变量

选取胶粘剂的类型、胶层的厚度、螺栓预紧力大小、螺栓孔直径为设计变量，通过DEP／Meshworks网格变形软件，建立车轮胶栓复合连接弯曲静力仿真的参数化模型，如图7所示。在胶接工艺中，胶层的厚度通过垫放金属丝来控制，可认为胶层的厚度符合正态分布，方差变异系数选为0.012。根据相关研究，螺栓预紧力具有分散性，呈正态分布［20］，设定其方差变异系数为0.010。加工过程中，尺寸参数一般存在加工误差，符合正态分布，设定螺栓孔直径的方差变异系数为0.010。胶粘剂的种类呈离散分布，各设计变量的取值如表1所示，胶粘剂1、2、3、4分别代表结构胶 A、B、C、D。

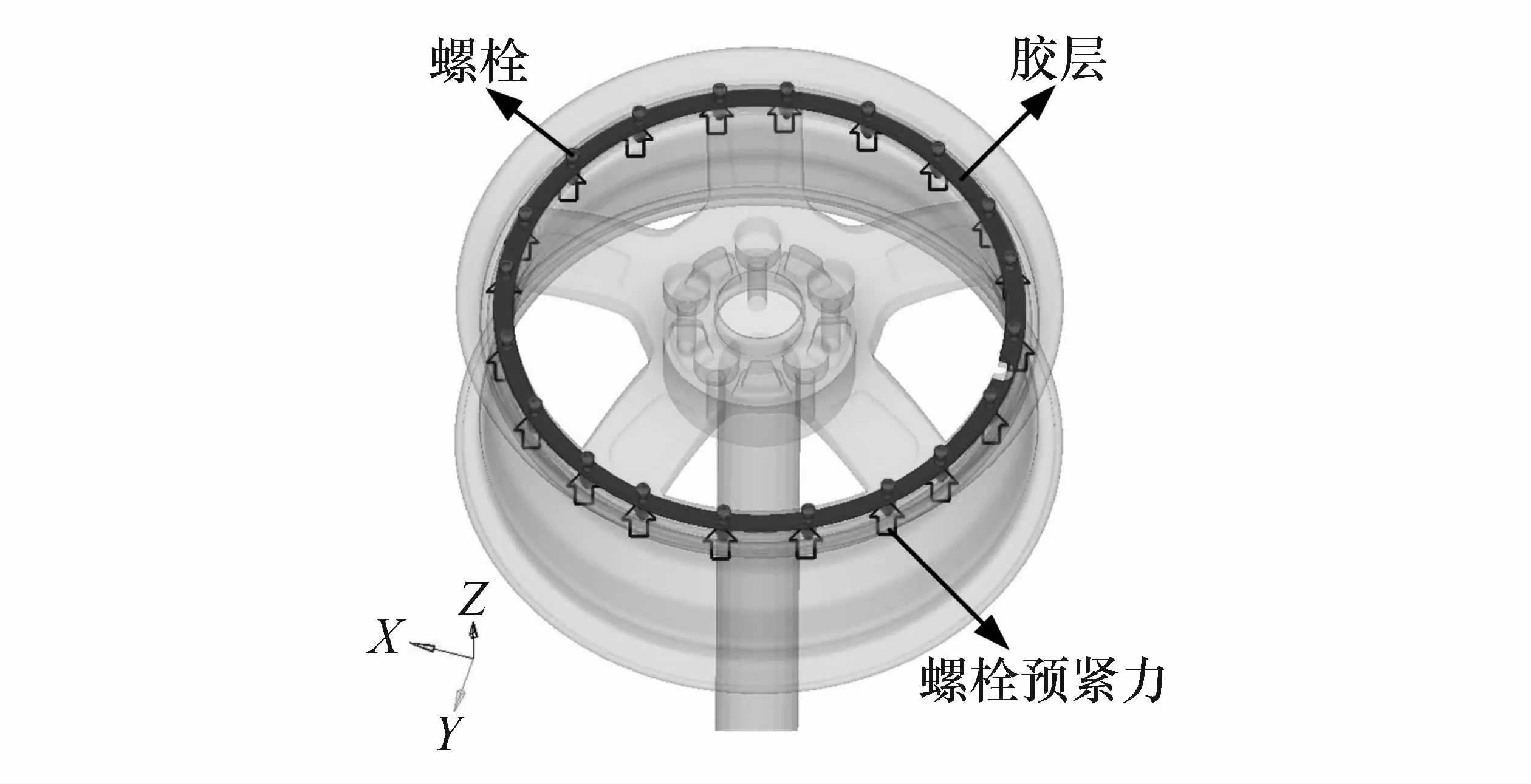
图7 车轮胶栓复合连接参数化模型

3.2 确定性和稳健性优化模型

由于螺栓的疲劳寿命与胶层的最大拉伸、最大剪切应力间存在着耦合和矛盾关系，对车轮进行栓胶复合连接多目标轻量化时，选取螺栓的疲劳寿命、胶层的拉伸应力和剪切应力为优化目标，以车轮结构不发生塑性变形、结构胶不发生断裂失效、车轮连接螺栓的疲劳寿命大于轮辐疲劳寿命（根据前文试验结果，轮辐疲劳寿命25万次，故连接螺栓的疲劳寿命应达30万次以上）为约束条件，建立的确定性优化模型如式（4）所示，建立的稳健性优化模型如式（5）所示。

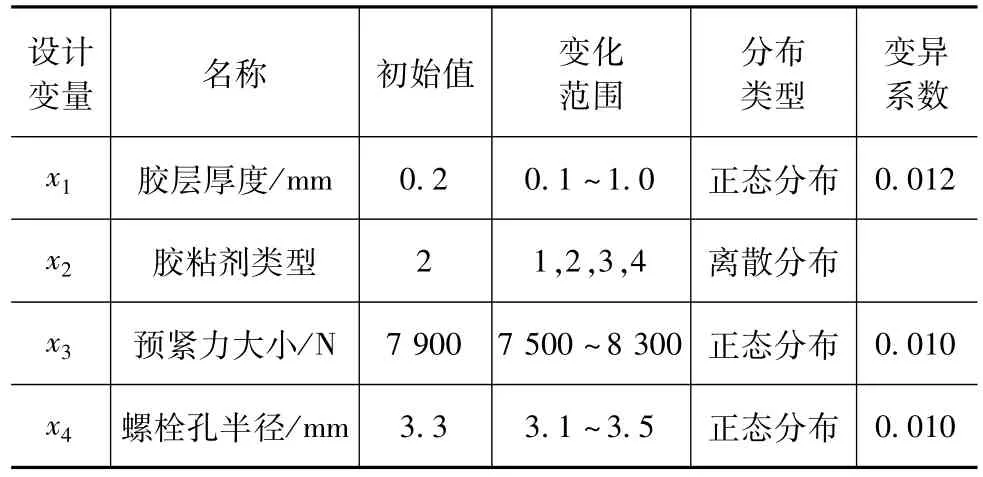
表1 各设计变量及取值范围

式中：m（x）为栓胶连接车轮总成的质量，kg；m0为栓胶连接车轮总成优化前的质量，kg；Nb（x）为螺栓的最小动态弯曲疲劳寿命，104万次；σa（x）、σs（x）、σr（x）、σb（x）分别为结构胶、轮辐、轮辋、螺栓在弯曲工况下的最大等效应力，MPa；［σ］a、［σ］s、［σ］r、［σ］b分别为结构胶、轮辐、轮辋、螺栓所用材料的许用应力，［σ］a＝46.8 MPa，［σ］s＝170 MPa，［σ］r＝190 MPa，［σ］b＝640 MPa；xL和 xU分别为设计变量x的取值下限和上限；μ为平均值；σ为标准差。

3.3 Kriging近似模型

采用最优拉丁方抽样方法在设计变量的取值空间内均匀采样，得到40组样本点来拟合各响应的Kriging近似模型，采用哈默斯雷抽样方法额外抽取30组样本点进行误差检验，检验原理如式（6）所示，以决定系数R2的值来评价近似模型精度，R2越接近1，近似模型的精度越高。通过检验，所建的12个响应值的决定系数均大于0.9，如表2所示，其中，螺栓的最小疲劳寿命、结构胶Z向最大拉伸应力近似模型的精度检验结果如图8所示。

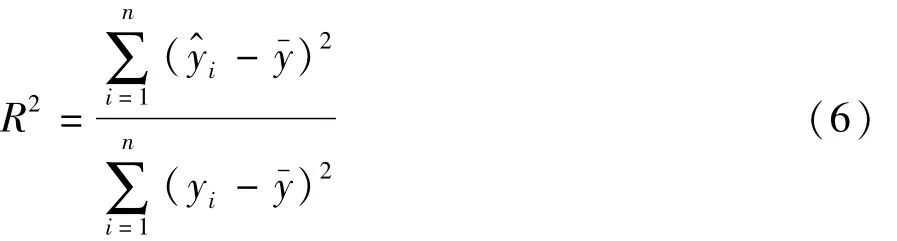
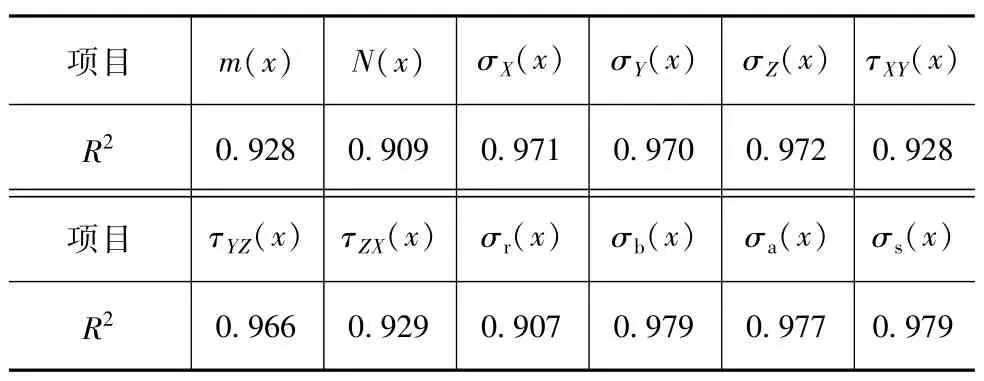
表2 近似模型误差分析结果

4 优化与讨论

使用多学科优化设计软件ISIGHT搭建车轮栓胶复合连接多目标优化平台，集成各性能指标的计算组件，结合第二代非支配排序遗传算法NSGA-II，对所建立的Kriging近似模型进行确定性多目标优化，优化分析模型如图9（a）所示。

多目标优化后，从Pareto解集中选取得到最优解，如表3所示。采用Monte-Carlo描述抽样方法对最优解进行6σ稳健性分析，由于变量x2胶层类型为离散分布，在6σ稳健性分析时，其取固定值4。稳健性分析结果表明，各输出响应的质量水平均达到8σ水平，螺栓的最小疲劳寿命提升至71.45万次，满足设计要求，胶层的等效应力、最大拉伸和剪切应力均在破坏强度内，胶层未发生失效。

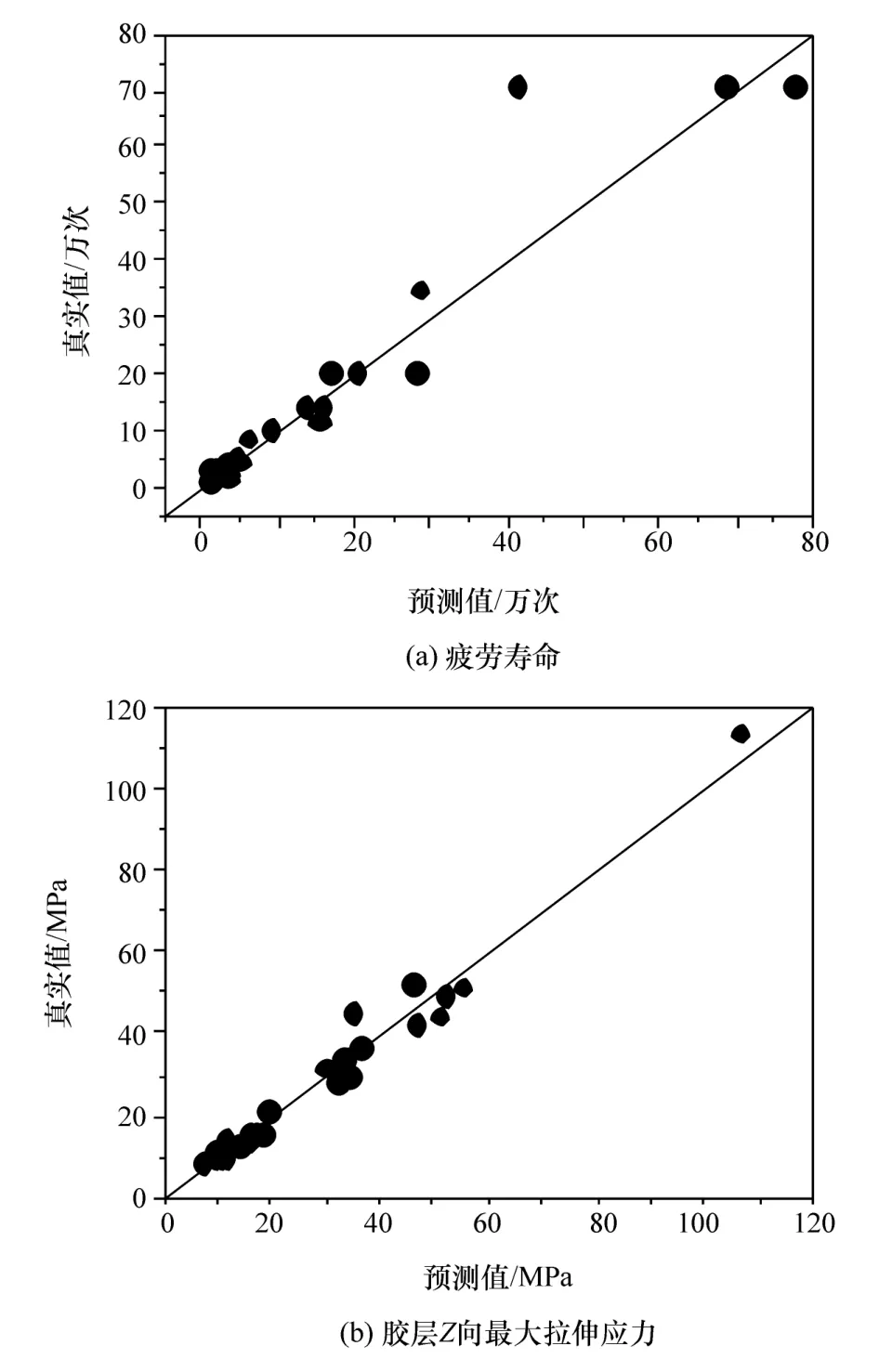
图8 Kriging模型精度检验结果

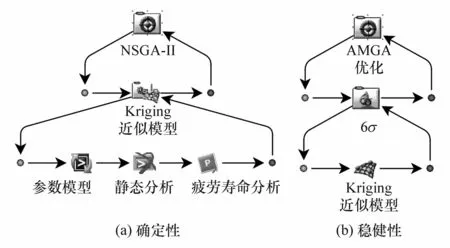
图9 多目标优化分析模型

基于6σ稳健性设计理论，采用Monte-Carlo描述抽样技术，结合微存档遗传算法AMGA对所建立的Kriging近似模型进行稳健性多目标优化，优化分析模型如图9（b）所示。优化后的结果如表3所示。

表3 确定性和稳健性优化设计结果

由表3可以看出，稳健性多目标优化后，各设计变量和输出响应的质量水平均控制在8σ水平。优化后螺栓的最小疲劳寿命为64.23万次，与确定性优化解相比，稳健性有所降低，两者的概率密度分布如图10（a）所示。优化后胶层的最大拉伸和剪切应力均略高于确定性优化解，但其稳健性得到有效提升，两者的概率密度分布如图10（b）和图10（c）所示。对于其他输出响应，稳健性优化的可靠性均高于确定性优化。从整个连接系统的可靠度出发，在螺栓疲劳寿命远大于设计要求的情况下，6σ稳健性优化结果的系统综合可靠性更优。从工程应用出发，和螺栓相比，结构胶在湿热或交变载荷环境下的敏感度更高，更易产生疲劳退化［21－22］，故胶层的可靠性优先度高于螺栓。综上，6σ稳健性优化有效降低车轮在复杂服役环境下的破坏几率。

5 结论

（1）使用名义应力法对组装式车轮和连接螺栓进行动态弯曲疲劳寿命仿真分析，将仿真结果与试验结果对比，验证了车轮仿真模型的准确性。

（2）将弹塑性模型作为胶层的本构模型，对哑铃型胶条标准样件进行拉伸试验，得到结构胶的应力应变曲线；对铝镁合金单搭接胶粘接头进行拉伸试验，得到结构胶的剪切强度。

（3）综合运用网格变形技术、Kriging近似模型理论和NSGA-II多目标优化算法，使用ISIGHT优化平台对车轮栓胶复合连接结构进行了确定性多目标优化。基于6σ稳健性设计理论，结合微存档遗传算法AMGA，对车轮胶栓复合连接结构进行了稳健性多目标优化，和确定性优化相比，车轮连接的可靠性得到进一步提升。

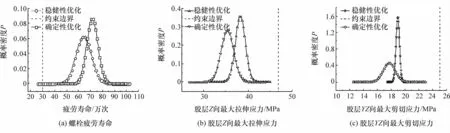
图10 确定性和稳健性优化的目标响应的概率密度分布