汽车滑移门典型关门驱动力构建的研究*

高云凯，袁 泽，段月星

（同济大学汽车学院，上海 201804）

前言

汽车滑移门系统因其开度大和开启后占用空间小等优点，目前在商务车、旅行车上得到了广泛应用。人在开启和关闭滑移门时要施加驱动力，这对滑移门导向系统的结构设计有着重要影响［1－2］。在滑移门前期开发阶段，符合实际的驱动力是滑移门导向系统动力学分析的前提和基础［3］。由于使用时所处环境不同，即使是同一个人，在操纵滑移门多次开闭的过程中施加的驱动力也不尽相同。在进行动力学分析时考虑计算成本，不可能将测得的驱动力全部施加于滑移门导向系统动力学模型中，而宜选取具有代表性的驱动力。因此，基于试验数据构建典型的驱动力能为滑移门导向系统动力学特性和耦合机制的研究提供可靠的输入数据，对滑移门导向系统动力学分析和优化具有重要意义。

目前，针对滑移门典型驱动力构建的相关研究较少。国内一些研究滑移门开闭性能的文献［4－6］使用STEP函数来定义驱动力—时间曲线，以模拟实际开关门过程，但力的大小和变化形式是根据经验得到的，因不同文献中驱动力峰值相差很大，会影响后续动力学分析结果的准确性。Chen等人［7］通过连接在门把手上的橡皮绳关门，并将测得的一次数据输入到ADAMS中。Gao等人［8］收集了几个使用者关门时的驱动力，并选取滑移门关门速度处于中间的驱动力作为仿真时的边界条件。然而，上述文献均未对滑移门在实际使用时的工况进行划分，无法得到不同工况下的典型驱动力。

为此，本文中提出了一种构建汽车滑移门典型关门驱动力的方法。由于人关门过程具有较强的随机性和无后效性，故可针对滑移门低、中和高速3种关门工况，将以力为序列的马尔可夫链方法运用到典型关门驱动力的构建中。最后，通过比较构建出的典型关门驱动力特征参数与试验数据的特征参数平均水平，验证本文所用方法的有效性。速关门工况（v200＜1.0 m／s）、中速关门工况（1.0 m／s≤v200≤1.3 m／s）和高速关门工况（v200＞1.3 m／s）。

踏板力传感器如图3所示，它和数采通道连接，以1 000 Hz频率测量关门时作用于门把手上3个方向的驱动分力，分别为纵向、横向和垂向驱动力，如图4所示。试验开始时，启动试验数据采集处理系统，人在车外拉门把手分别以低速、中速和高速关门。试验结束后，对无法判断识别门把手作用力时刻、关门驱动力与关门速度方向不相符的试验数据进行初步筛除，共获取173组关门驱动力数据。其中，低速关门工况56组，中速关门工况74组，高速关门工况43组。

图2 测速仪与支架

图3 踏板力传感器

1 试验数据采集与预处理

1.1 试验数据采集

以某品牌MPV车作为试验对象对滑移门关门驱动力曲线进行采集，见图1。

图1 试验对象

根据工程上滑移门使用寿命经验和其滚轮的磨损情况，同时为便于滑移门关闭性能分析，以滑移门距离全关位置200 mm处测得的关门速度作为划分滑移门关门工况的依据。此位置处滑移门的关门速度可由测速仪测量得到，测速仪和支架布置如图2所示。这样，可将滑移门分为3种主要关门工况：低

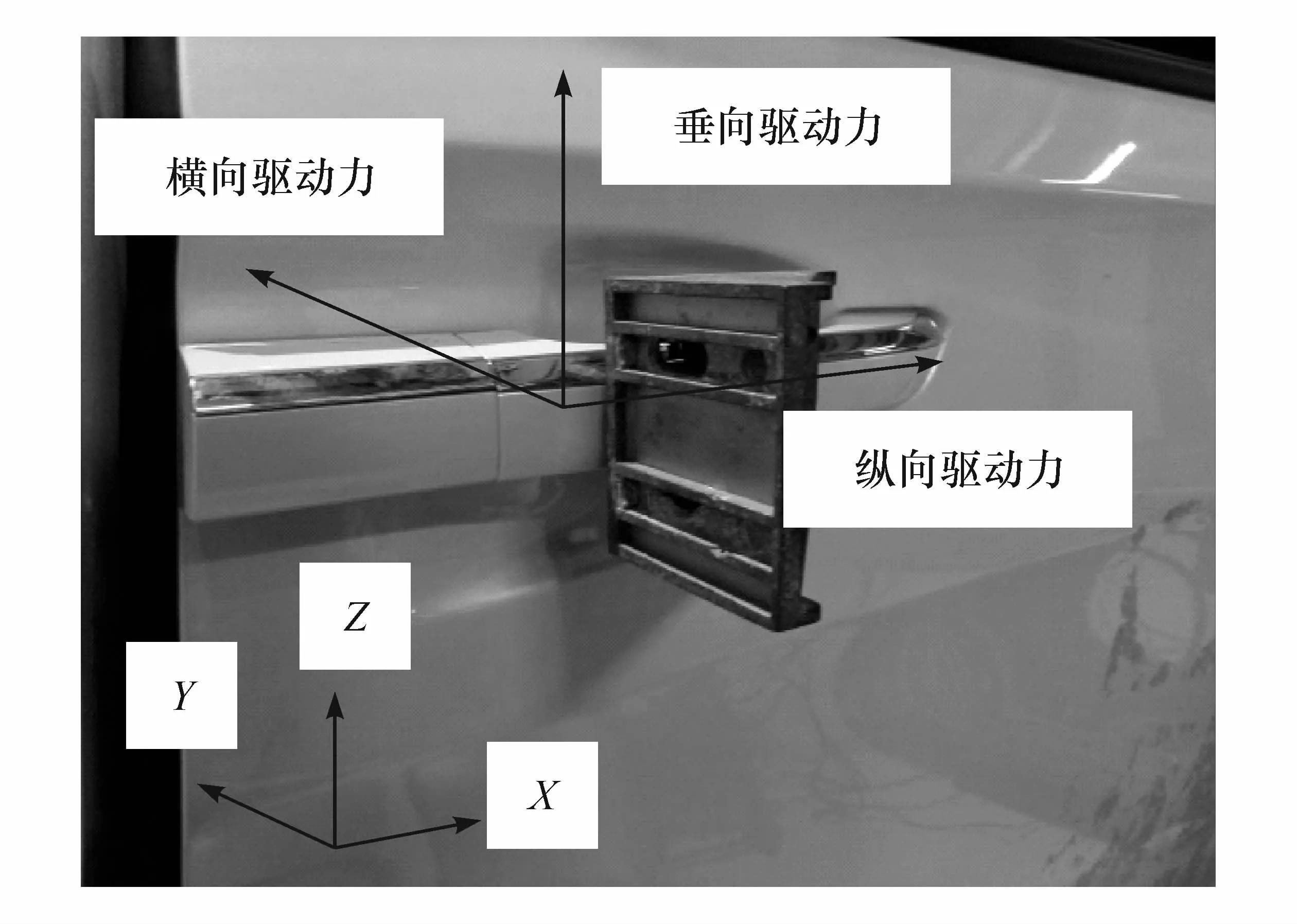
图4 作用在门把手上的纵向、横向和垂向驱动力

1.2 特征参数选取

试验采集得到的关门驱动力曲线所包含研究对象的信息是最完整和全面的，图5所示为低速关门工况驱动力曲线。然而直接用其来分析关门驱动力特性会比较困难，因此须从曲线中提取出一些能涵盖其所有重要信息的特征参数，以便利用这些特征参数完全代替曲线来对关门驱动力特性进行定量分析，使可运用的统计学方法大大增多。不过要涵盖曲线所有重要的信息，不能仅仅选取关门驱动力或时间和曲线斜率等单一特征参数的集合，而应该综合关门驱动力大小、持续时间长短、关门力变化率和冲量大小等描述曲线的参数。为了详细反映关门驱动力的瞬时特征和整体特征，同时根据工程经验，本文中对纵向和横向驱动力各引入了10个特征参数：持续时间T／s、关门驱动力平均值Fa／N、关门驱动力峰值 Fmax／N、整个关门过程冲量 I／（N·s）、关门驱动力减小总时间Ta／s、关门驱动力增加总时间Td／s、曲线斜率最大值 amax／（m·s－2）、曲线斜率最小值amin／（m·s－2）、曲线正斜率平均值 aa／（m·s－2）、曲线负斜率平均值 ad／（m·s－2）；由于垂向驱动力曲线的峰值和力增减时间特征并不明显，故只选取5个特征参数：持续时间T／s、垂向关门驱动力平均值Fz／N、关门过程冲量 Iz／（N·s）、曲线正斜率平均值aza／（m·s－2）、曲线负斜率平均值 azd／（m·s－2）。

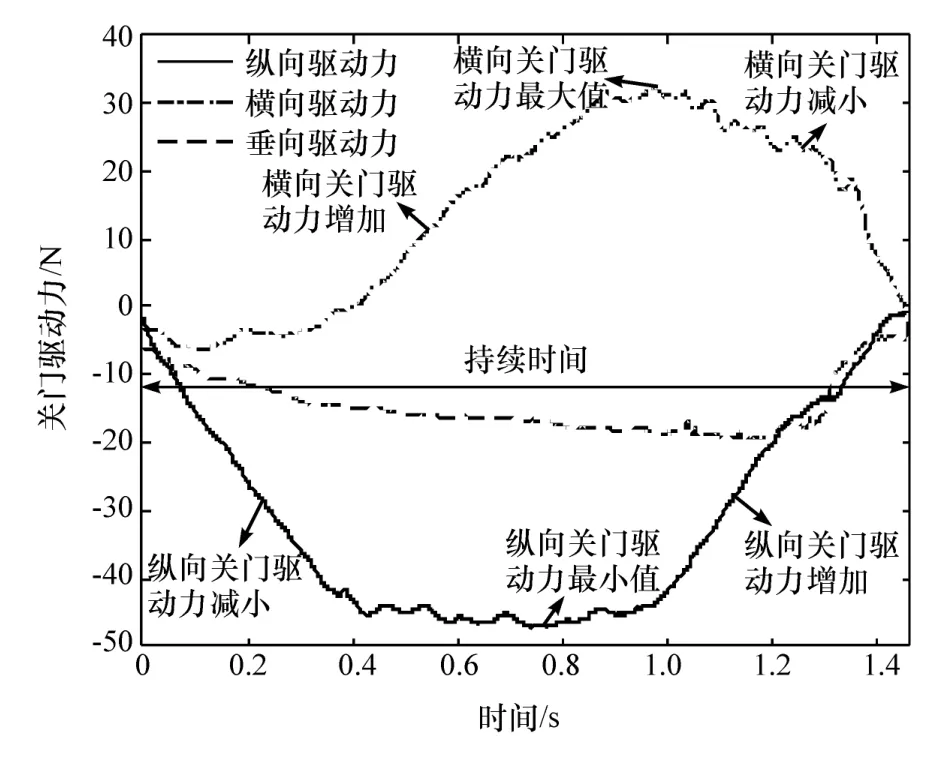
图5 低速关门工况驱动力曲线

通过试验数据构造出3种关门工况驱动力曲线的参数矩阵 Zmk×l：

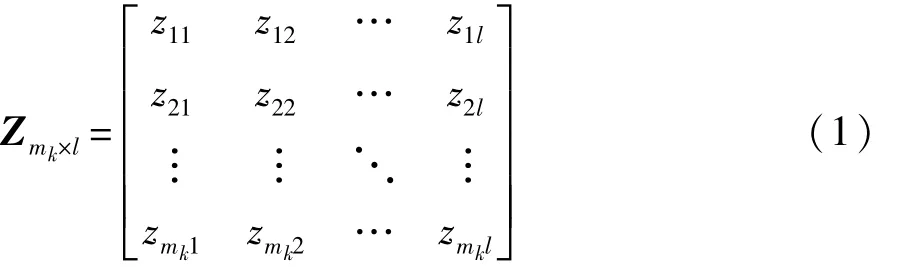
式中：zij（i＝1，2，…，mk，j＝1，2，…，l）为第 i条曲线的第j个参数；k＝1，2，3分别代表低速、中速和高速关门工况；mk为对应关门工况驱动力曲线数目；l为引入的特征参数个数。

1.3 异常值剔除与参数标准化

在对3种关门工况下的特征参数分别进行分析时，会发现某些曲线中的一些特征参数的波动规律与其他特征参数所呈现的规律明显不同，这时就须将这些异常值剔除，以避免其影响后续的主成分分析与典型关门驱动力的构建。本文中采用PauTa法则进行异常值剔除，如果某个特征参数zij满足如下公式：

其中

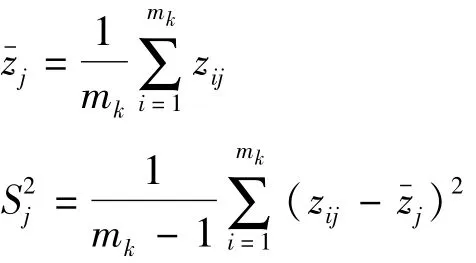
则认为zij是异常值，应予剔除。异常值剔除后，低、中和高速关门工况下驱动力曲线数目变为m′1、m′2和 m′3，其中 m′1＝55，m′2＝69，m′3＝42。

由于各个特征参数之间量纲不同，同时取值范围也存在差异，为消除它们对处理结果稳定性产生的影响，对上述矩阵进行标准化得到矩阵

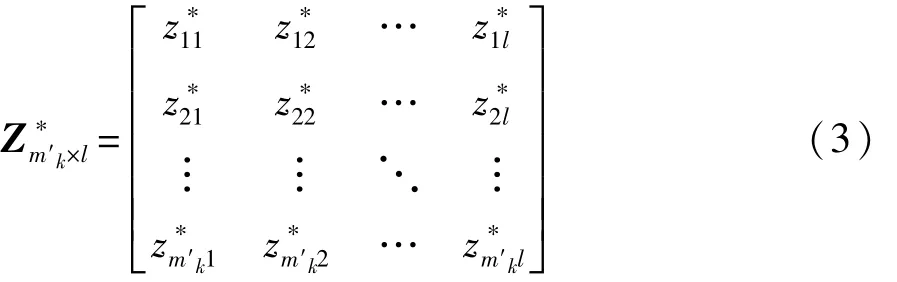
表1所示为低速关门工况下纵向驱动力曲线10个特征参数的标准化矩阵Z*55×10。

表1 特征参数标准化矩阵55×10

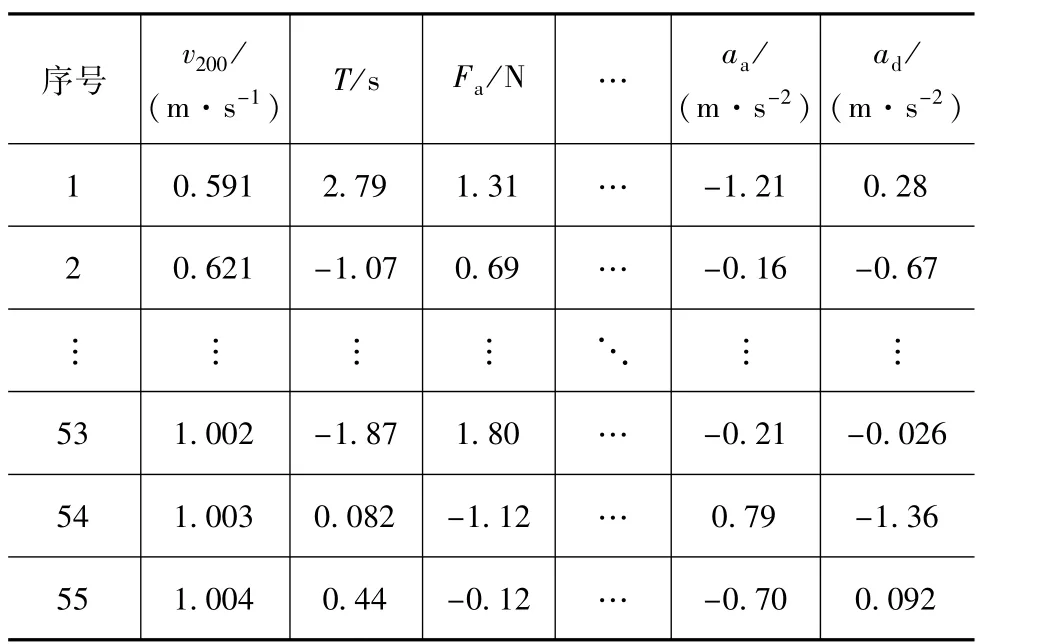
表1 特征参数标准化矩阵55×10

序号 v200／（m·s－1） T／s F a／N … a a／（m·s－2）a d／（m·s－2）1 0.591 2.79 1.31 … －1.21 0.28 2 0.621－1.07 0.69 … 53 1.002－1.87 1.80 …－0.16 －0.67⋱－0.21 －0.026 54 1.003 0.082 －1.12 …0.79 －1.36 55 1.004 0.44－0.12 … －0.70 0.092

2 典型关门驱动力的构建

2.1 马尔可夫链原理与驱动力构建流程

马尔可夫过程是典型的随机过程，它的主要特征是具有无后效性［9］，即：过程在t0时刻所处状态为已知的条件下，在t＞t0时刻所处状态的条件分布与t0时刻之前所处的状态无关。当马尔可夫过程中的时间与状态均为离散时，则称为马尔可夫链。

人拉滑移门门把手时施加的关门驱动力随机性较强，且当前的驱动力状态只和前一时刻的驱动力状态有关，具有马尔可夫性。在进行滑移门关门试验时，踏板力传感器每隔相同的时间就记录一次试验数据，这样时间和关门驱动力的变化均可看作是离散的，驱动力F的变化过程可表示为时间t的一个序列｛…，Ft－2，Ft－1，Ft，Ft＋1，Ft＋2，…｝。因此，可利用马尔可夫链进行各工况下典型关门驱动力的构建，构建流程如图6所示。

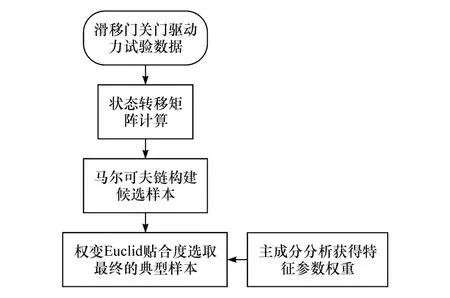
图6 马尔可夫链构建典型关门驱动力流程图

2.2 状态转移概率矩阵求解

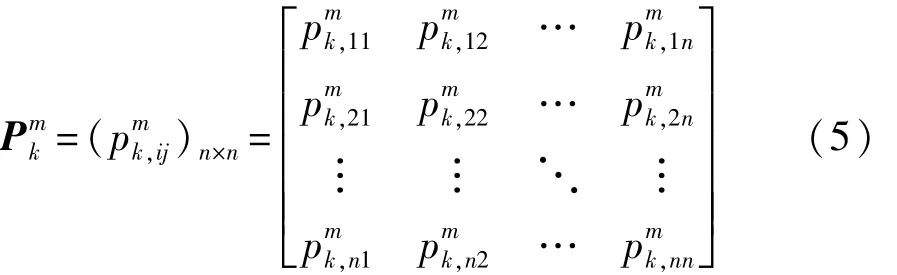
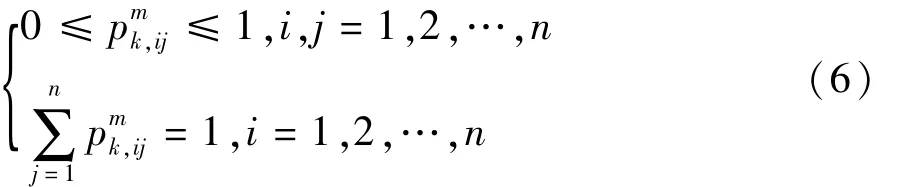
关门驱动力状态划分是利用马尔可夫链方法中非常重要的一环。根据理论，数据越多，数据状态划分得越细，预测准确度就会越高。然而，如果状态划分得太细，就会造成每个状态的数据点过少，转移概率失去规律性［10］。为保证计算精度，综合每种速度工况的关门驱动力范围与数据样本个数等因素，将低速关门工况的纵向、横向、垂向驱动力分别划分为25，28，18个状态，中速关门工况的3个方向驱动力分别划分为20，24，20个状态，高速关门工况的3个方向驱动力分别划分为25，34，22个状态。在MATLAB中编写程序，计算每种工况下每个方向状态转移概率矩阵Pmk，图7所示为低速关门工况下的纵向驱动力状态5、状态10和状态20时的转移概率曲线。由图可见，状态转移概率基本上都分布在当前状态下，这说明关门驱动力一般都是渐进变化的，与人拉车门把手的规律相符。

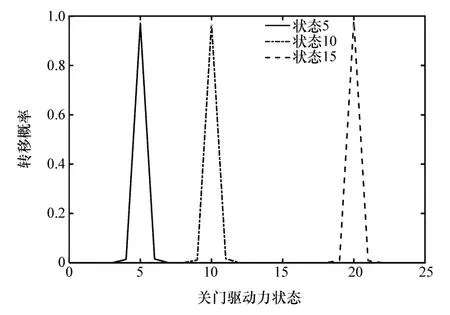
图7 状态、和时的转移概率分布曲线

2.3 关门驱动力候选曲线生成

在求解出状态转移概率矩阵和各个状态转移概率分布曲线后，进行各工况下候选关门驱动力的构建，具体步骤如下。

（1）确定关门驱动力的初始状态。当人拉滑移门门把手进行关门时，驱动力的初始值为0。由于低速关门工况的纵向驱动力值在［－80 20）之间，被划分为25个状态，故此时初始状态已知初始状态即可计算下个时刻的状态

（2）利用MATLAB中的rand函数生成当前关门驱动力状态服从均匀分布 U（0，1）的随机数r。按照式（8）利用状态转移概率矩阵对从当前状态转到下一时刻任一状态的概率进行累加，u代表累加次数，直到该累加值大于生成的随机数r，此时＝u。

2.4 典型关门驱动力选取

本文中每种工况每个方向都生成了10 000条候选驱动力—时间曲线，须根据权变Euclid贴合度方法从中选择一条最具代表性的关门驱动力曲线，而该方法中特征参数的权重则由主成分分析法获得。

由于从曲线中提取出的特征参数能描述的信息量不同，即它们的重要程度不同，所以要赋给其不同的权重。用主成分分析法确定权重首先须求出主成分的方差贡献率和每个特征参数在各主成分线性组合中的系数。由前面可知，对应工况下各方向关门驱动力数据的标准化矩阵为，由此计算协方差矩阵：

其中

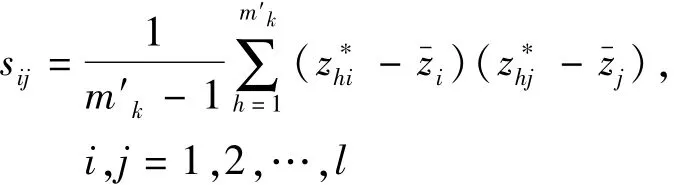
用λi表示协方差矩阵Σ的特征值λ1≥λ2≥…≥λl≥0，即为l个主成分对应的方差。计算出λi对应的单位化特征向量 ei＝｛e1′i，e2′i，…，et，i｝，则由此所确定的主成分为

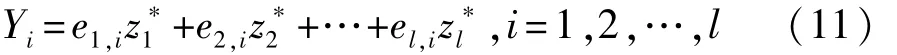
式中：Yi为第i个主成分为标准化后的第i个特征参数。主成分分析把l个特征参数的 方差之和

这里的总方差tr（Σ）分解成了l个相互独立的变量Y1，为第k个主成分Yk的贡献率，贡献率越大则代表该主成分描述的信息越多。若只取前m个主成分，则累计贡

通过对每个工况各方向驱动力的特征参数进行主成分分析，可获得各主成分特征值、贡献率和累计贡献率。表2所示为低速关门工况下纵向驱动力的各主成分情况。

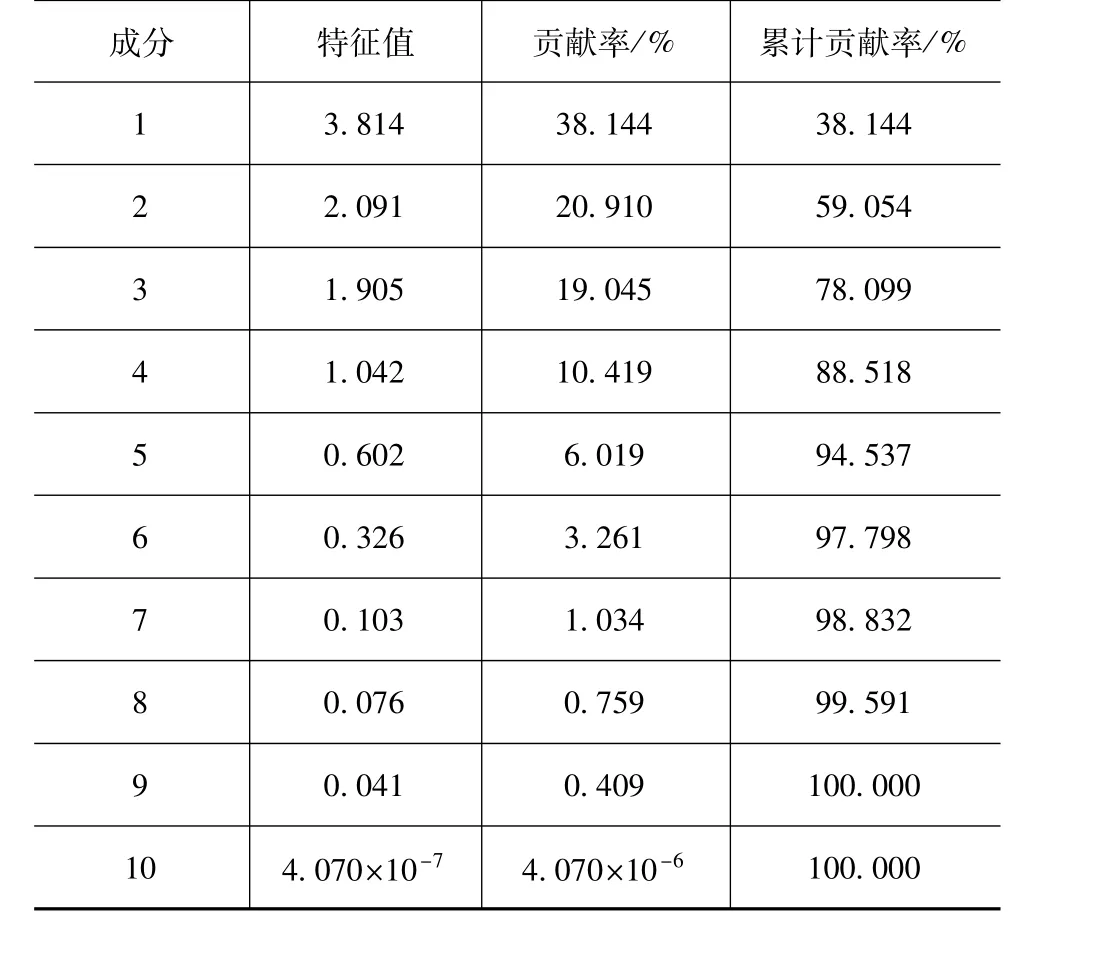
表2 主成分贡献率和累计贡献率

从理论上讲，各成分特征值在1以上，累计贡献率达到85%以上［12］，对最终结果的影响就很小。由表2可见，前4个主成分的累计贡献率已达88.518%，同时特征值都大于1。因此，选取前4个主成分即可代表一条关门驱动力曲线的大部分信息。

为建立选取的4个主成分与10个特征参数的表达式，得到成分得分系数矩阵R如表3所示。

得到了4个主成分的方差贡献率和每个特征参数在各主成分线性组合中的系数rij后，按式（12）计算第i个特征参数的系数αi：

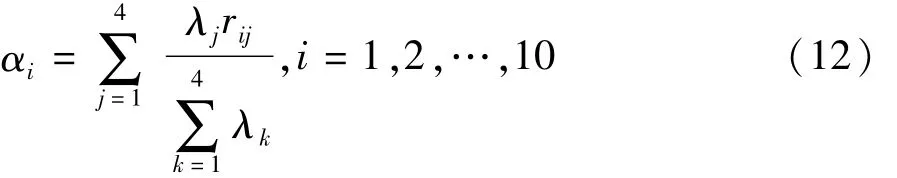
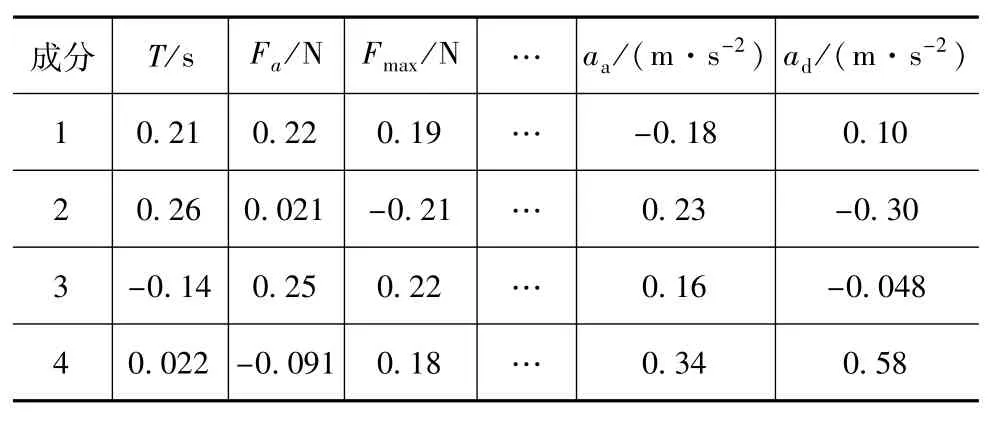
表3 成分得分系数矩阵R

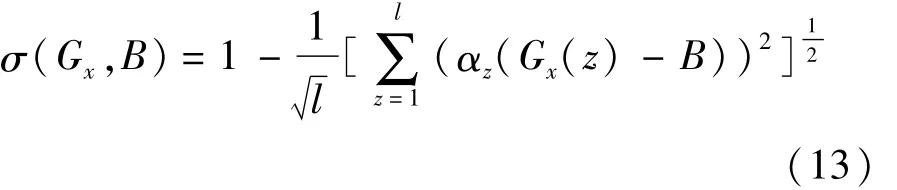
在对10个特征参数的系数进行归一化后，便能得到它们所占权重。将求出的权重代入式（13）计算权变Euclid贴合度：式中：σ为生成的候选关门驱动力与试验得到的关门驱动力之间的贴合度；Gx为生成的第x个候选样本数据；B为特征参数接近平均水平的一次试验数据；αz为第z个特征参数的权重；l代表选取的特征参数数目。将生成的10 000个候选样本数据代入到式（13）中，若 σ（Gd，B）＝max｛σ（G1，B），σ（G2，B），…，σ（Gn，B）｝，其中 n为候选样本数据总数，则选取Gd为典型关门驱动力。

根据上述步骤最终得到3种工况下纵向、横向和垂向典型关门驱动力曲线，如图8所示。

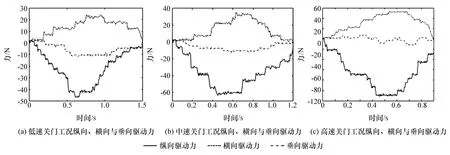
图8 3种工况下典型关门驱动力曲线

由图8可见，随着关门速度的增加，纵向和横向关门驱动力增大，而垂向关门驱动力则没有明显变化。注意到横向关门驱动力为正值，这说明在关门时使用者都有将滑移门向车内推的习惯。低速关门工况下，人在实际使用时作用于门把手的纵向、横向和垂向驱动力峰值分别为－46、25和－10 N左右；在中速关门工况下纵向、横向和垂向驱动力峰值分别为－65、37和－12 N左右；在高速关门工况下纵向、横向和垂向驱动力峰值则分别为－112、53和－16 N左右。3种工况下纵向关门驱动力峰值约为横向关门驱动力峰值的2倍，为垂向关门驱动力峰值的5～7倍。另外，人作用于门把手的持续时间会随着关门速度的增加下降，且在中高速关门工况下驱动力达到峰值的时间比在低速关门工况时稍短。

3 关门驱动力曲线拟合

构建出的典型关门驱动力曲线是不光滑的且有波动，但关门驱动力通常要满足尽量简单的特点，以便于工程上能实现对其的加载。因此，根据图8中关门驱动力曲线特征，对典型关门驱动力曲线进行拟合。与纵向、横向驱动力相比，垂向驱动力峰值较小，所以在低速和中速关门工况下使用STEP函数拟合，在高速工况可直接视为0水平函数。而纵向和横向驱动力则采用最小二乘法将其拟合成1阶线性V形函数和STEP函数两种形式。为比较两种拟合形式与典型关门驱动力曲线的吻合程度，采用均方根误差（RMSE）作为拟合误差比较准则，其公式为

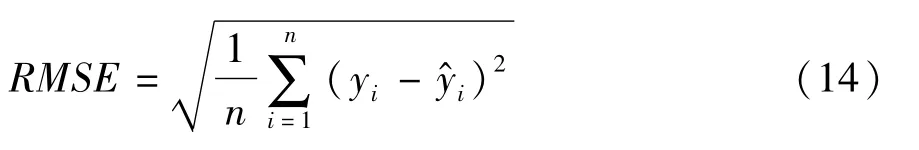
式中：yi为原始数据；为拟合数据。

由表4可见，使用STEP函数对典型关门驱动力曲线进行拟合的均方根误差比V形函数的小，拟合结果准确度高。另外，通过ADAMS／Step模块即可实现拟合函数的加载，具有较高的可行性。用STEP函数拟合后的典型关门驱动力如图9所示。

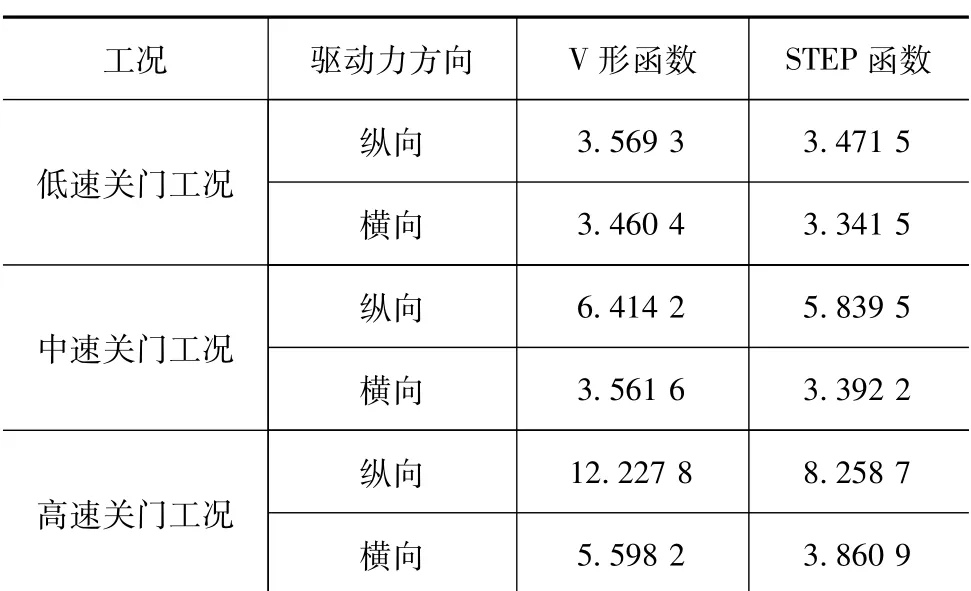
表4 两种拟合方式的均方根误差

4 有效性验证

为检验所用方法的有效性与合理性，求出了构建的滑移门典型关门驱动力特征参数与对应工况下特征参数平均水平的相对误差，表5所示为低速关门工况纵向驱动力特征参数的对比。其中，本文方法的数据是采用马尔可夫链方法构建的典型关门驱动力曲线的10个特征参数，平均水平的数据则是对对应工况的所有试验数据曲线的每个特征参数求平均值而得。

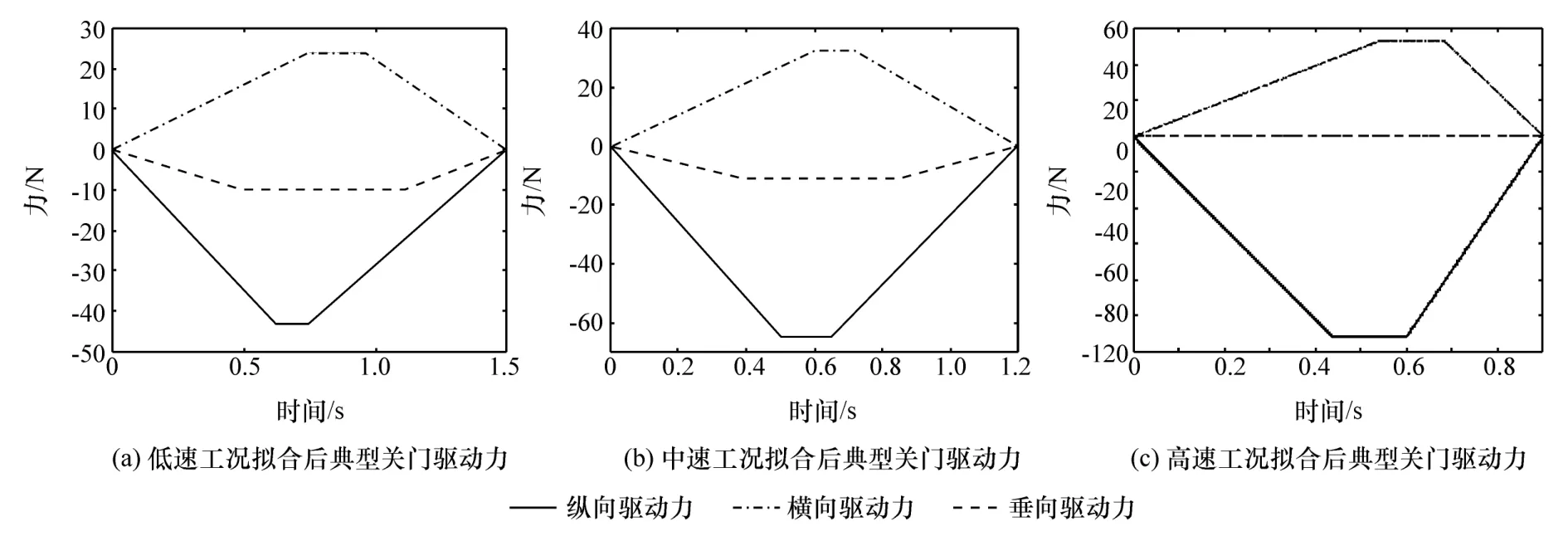
图9 3种工况下关门驱动力拟合函数

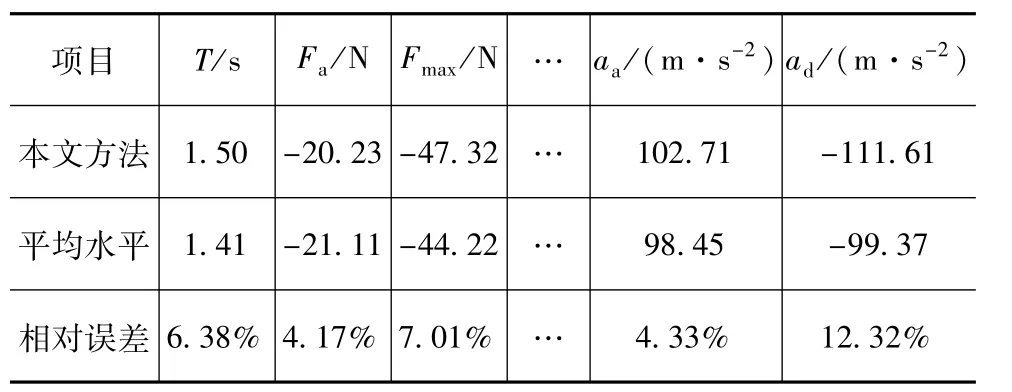
表5 低速关门工况纵向驱动力特征参数对比

由表5可见，构建的低速关门工况纵向驱动力特征参数与该工况下平均特征参数的相对误差较小，在考虑每个特征参数的权重后整体相对误差为5.37%。另外，其余关门工况各方向驱动力的整体相对误差也均在10%以内，表明本文所用方法构建的关门驱动力具有典型性。

在把典型关门驱动力曲线拟合成STEP函数后，须将拟合函数与试验数据平均水平进行比较以检验拟合的可行性与准确性。从表4可以看出，高速关门工况纵向驱动力的均方根误差最大，拟合效果比其他的要差，因此对其进行验证。由于关门驱动力拟合函数是光滑且没有波动的，与函数斜率有关的特征参数对比无法体现与试验数据平均水平的本质差异，因此本文中选用驱动力平均值、驱动力峰值和关门过程冲量3个特征参数做误差分析。表6所示为拟合后的高速关门工况纵向驱动力特征参数与该工况平均水平的对比。

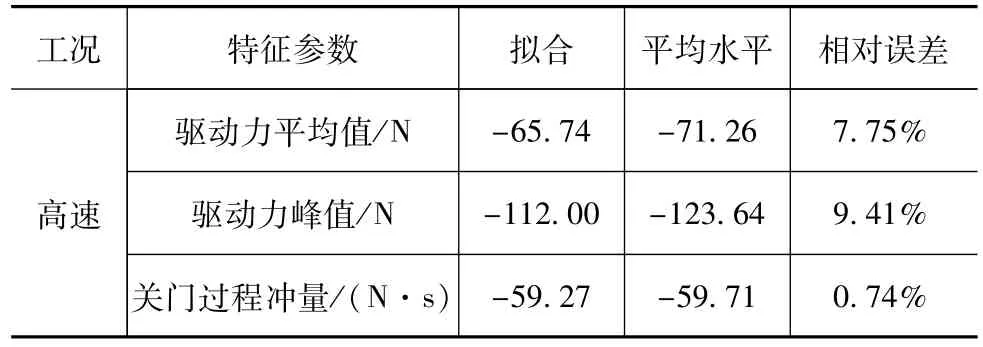
表6 拟合函数特征参数与平均水平对比

由表6可见，拟合后的高速关门工况纵向驱动力特征参数与平均水平的最大相对误差在10%以内，满足输入到滑移门动力学模型和工程上加载的精度要求。

5 结论

本文中基于某MPV车的滑移门关门驱动力试验数据，采用以力为序列的马尔可夫链方法构建出滑移门典型关门驱动力并拟合成STEP函数形式。将该典型关门驱动力曲线和拟合函数的特征参数与对应工况的特征参数平均水平进行对比，结果表明整体相对误差均在10%以内，构建方法具有有效性。

与直接使用一条试验驱动力曲线或根据经验构建STEP函数形式的滑移门导向系统动力学模型相比，该方法构建的3种工况下典型关门驱动力能为滑移门导向系统动力学特性和耦合机制的研究提供更真实可靠的输入数据，对后续的滑移门导向系统动力学分析与优化具有重要意义。