车内低频振动噪声的虚拟传递路径分析*

唐中华，张志飞，陈 钊，蒲弘杰，李 云，徐中明

（1.重庆大学汽车工程学院，重庆 400030； 2.东风柳州汽车有限公司，柳州 545005）

前言

随着汽车 NVH（noise，vibration，harshness）性能日益受到用户的关注，且已成为汽车的主要性能之一，因此，如何快速及更早地发现并改善NVH问题显得至关重要［1］。

车内某点的振动噪声响应是由不同激励源沿特定路径传递至该点后叠加的结果［2］，而传递路径分析法（transfer path analysis，TPA）是诊断汽车振动噪声问题准确有效的方法［3］。通过分析各传递路径对总响应的贡献量，找出起主导作用的路径［4］，指导设计，从而提升整车NVH性能。如解决转向盘抖动问题［5］、减小发动机燃烧激励产生的“隆隆”声［6］等。但目前应用较多的传递路径分析方法均以试验数据为基础［7－10］，可统称为试验 TPA，而试验数据获取耗时耗力，因此，将试验数据与仿真结合的混合TPA［11－12］在一定程度上能够缩短试验时间，提高效率。

由于试验TPA与混合TPA均依赖于试验数据，而在整车开发初期，缺少样车，无法获取相应的试验数据，因此，虚拟传递路径分析法被提出以诊断车内振动噪声问题。虚拟TPA在整车开发初期可有效诊断整车NVH问题，为整车设计提供参考。祖庆华［13］运用整车多体动力学模型提取工作载荷，并结合整车— 固耦合模型，对整车做了虚拟传递路径分析。何智成等［14］采用多体动力学方法和有限元法建立了整车刚柔耦合模型，并运用传递路径分析法对动力传动系统参数进行了匹配优化。但由于激励载荷提取和路径传递函数计算未在同时完成，仿真模型的建立和不同数据间的转换、衔接须花费较长时间，分析效率较低，因此，建立基于有限元法的整车NVH模型对整车分析意义重大。

为实现在设计阶段开展整车传递路径分析且避免数据间的转换、衔接以提高效率，运用有限元法建立包含车身、底盘和声腔的整车虚拟传递路径分析模型，并通过与频率响应法结果对比以验证虚拟TPA模型的正确性。然后运用该模型对车内响应峰值作传递路径分析，根据分析结果，找出引起该峰值响应的主要路径，并对主要路径上车身与底盘耦合的衬套参数进行优化，以改善车内振动噪声问题。

1 整车虚拟TPA模型建立

1.1 整车有限元建模

在hypermesh中，建立包含底盘的整车有限元模型，包括白车身、开闭件、声腔和底盘系统。

白车身和开闭件主要由钣金件构成，采用基本尺寸10 mm的壳单元建立有限元模型，并在车身上附集中质量模拟内外饰及电器附件。选择基本尺寸50 mm的实体单元建立声腔模型，并通过ACMODL卡片将车身和声腔模型耦合形成内饰车身声 固耦合模型［15］。

在内饰车身基础上，建立底盘系统形成整车NVH有限元模型。底盘系统主要包括动力总成、悬架系统和转向系统建模。由于主要考虑一般匀速行驶工况下路面激励的影响，因此以集中质量附转动惯量的方式模拟动力总成。采用滑动柱铰并附阻尼系数建立减振器模型，并用弹簧单元模拟减振弹簧组成悬架系统。转向系统采用壳单元与体单元建模，并用MPC模拟转向传动比关系。用集中质量模拟轮胎和轮辋。车身与底盘连接的橡胶衬套采用CBUSH单元模拟，并赋予实际的衬套刚度值。

最后建成整车模型如图1所示，共1 212 726个壳单元，1 655 851个体单元。其中57 604个三角形单元，1 155 122个四边形单元。主要材料参数如表1所示。

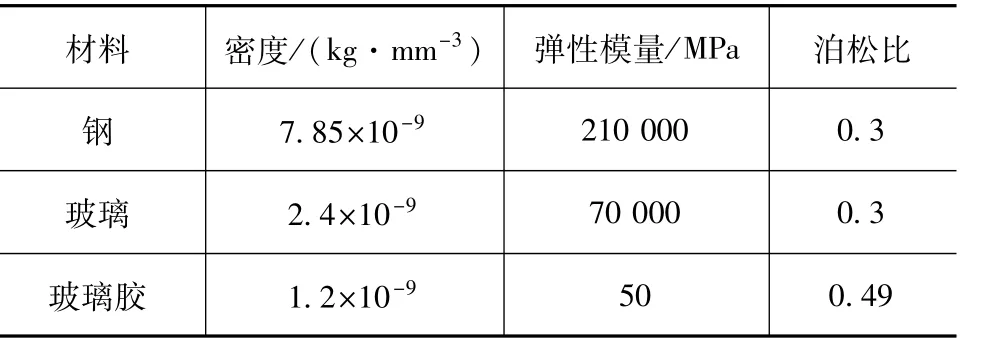
表1 主要材料参数

1.2 车内振动噪声响应预测

选取整车有限元模型4个轮心为激励点，分别施加Z向的单位白噪声激励来分析一般匀速行驶工况下路面激励的影响。单位白噪声激励频率范围为20～200 Hz，然后在Optistruct求解器中采用频率响应法［16－17］计算驾驶员右耳声压和驾驶员座椅导轨Z向振动响应，计算结果见图2。

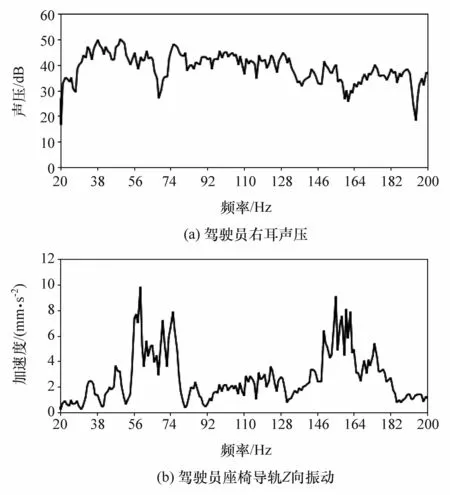
图2 车内振动噪声响应预测结果

在单位白噪声激励下，驾驶员右耳在38和48 Hz出现50 dB左右的峰值，而驾驶员座椅导轨在59 Hz处存在明显尖锐峰值，影响汽车的NVH性能。为查找峰值产生的原因，采用虚拟传递路径分析法作诊断分析。

1.3 虚拟传递路径分析法

车内总响应受激励源载荷与载荷传递路径共同影响。激励源包括振动源和噪声源，在此只考虑振动源，每个振动源通过结构路径向车内辐射噪声或引起车内部件振动。

振动源与响应点分别属于两个不同系统，两者在耦合处通过耦合元件（如衬套、铰链等）相连接。耦合处的每个自由度到车内响应点均形成一条传递路径。通常仅考虑3向的平动自由度，而忽略转动自由度［18］。假设有n条传递路径，第i条路径在车内的响应Pi为

式中：Hi（ω）为第 i条路径传递函数；Fi（ω）为该路径激励载荷。车内某点总响应Ptotal为各条路径响应的矢量和：

根据相位加权理论［19］，在某一频率下，第i条路径响应Pi与总响应Ptotal之间的相位夹角为θi，并以Ptotal方向为起始方向，逆时针为正向。

当 0°≤｜θi｜＜90°时，Pi在 Ptotal上投影为正，即贡献量为正值；90°＜｜θi｜≤180°时，Pi在 Ptotal上投影为负，即贡献量为负值；｜θi｜＝90°时，Pi在 Ptotal上投影为零，即贡献量为零。因此，响应幅值大的路径贡献量不一定大，贡献量还与相位角有关。某频率下第i条路径对总响应的贡献量Ci为

传递路径分析主要包含两部分工作，即路径传递函数计算和激励载荷提取。路径传递函数可由试验或数值计算获得，而提取激励载荷可通过直接测量法、动态复刚度法、矩阵求逆法和激励点反演法等［18］。

虚拟传递路径分析法的传递函数计算和激励载荷提取均在有限元计算中完成，即直接输出节点力作为激励载荷，类似于试验直接测量法获取激励载荷，而路径传递函数采用频率响应法计算。最后依据式（1）～式（3）计算总响应和各路径贡献量。

1.4 整车虚拟TPA模型建立

在整车声 固耦合模型基础上建立整车虚拟传递路径模型，并分析车内振动噪声问题。选取如表2所示的底盘与车身连接的18处耦合点作为激励点，驾驶员右耳和驾驶员座椅导轨为响应点，并建立如图3所示的TPA模型。考虑每个耦合点x、y、z 3个方向的平动自由度，因此每个响应点共有18×3＝54条路径。

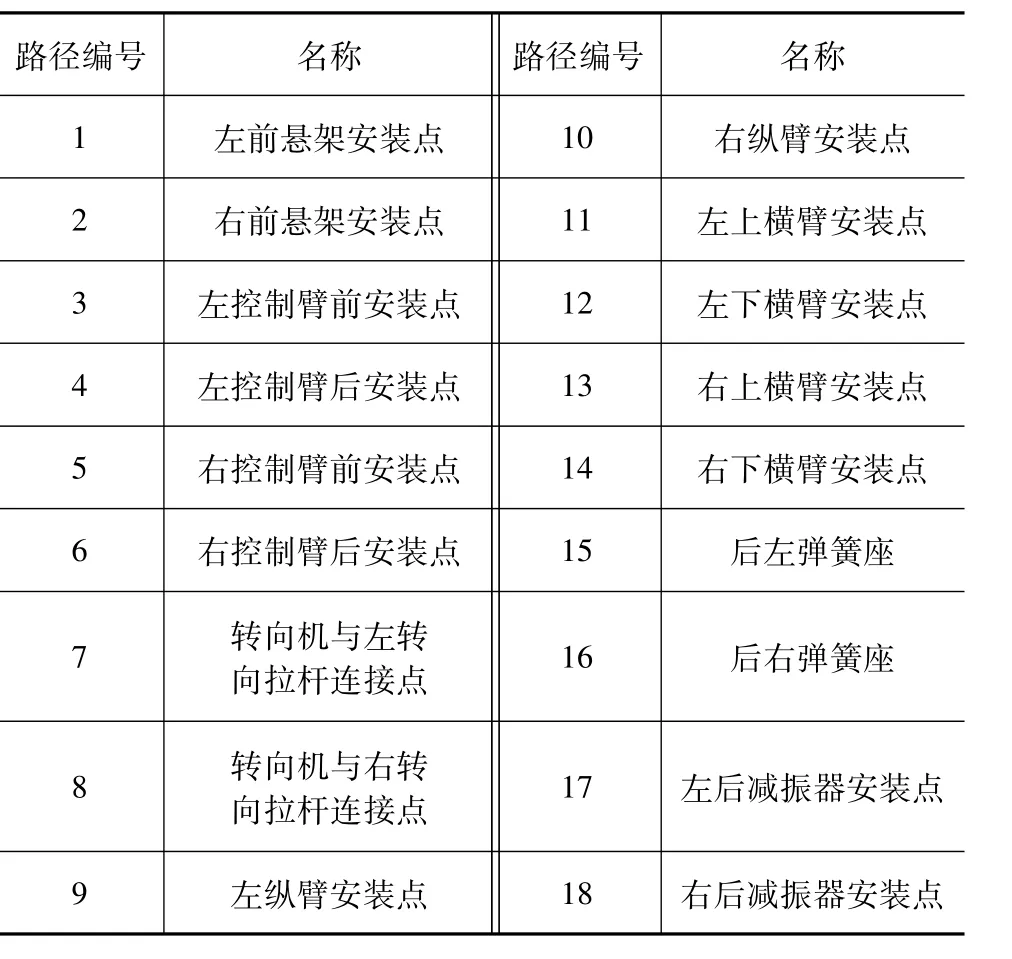
表2 路径与编号

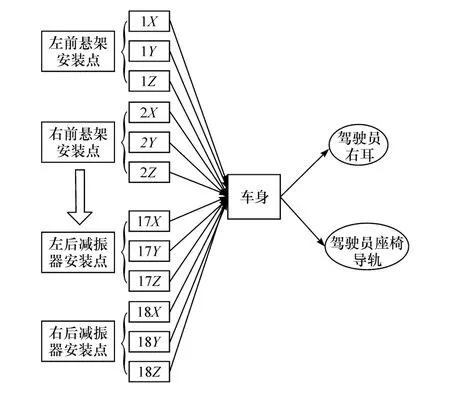
图3 整车虚拟传递路径示意图

2 结果分析

2.1 虚拟TPA模型验证

为验证虚拟传递路径模型的正确性，将虚拟传递路径法合成的车内声学振动响应与频率响应法结果进行对比，结果如图4所示。

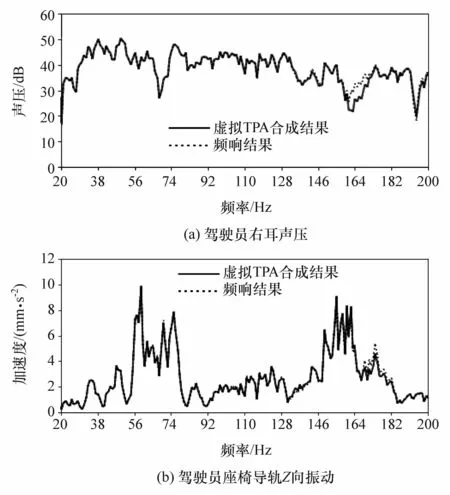
图4 频响法与虚拟TPA结果对比

虚拟TPA合成结果与频响结果两者吻合较好，说明传递路径选择正确，因此虚拟TPA模型可用来诊断车内振动噪声问题。以38 Hz处驾驶员右耳声压峰值和驾驶员座椅导轨Z向振动59 Hz处的峰值为例，分析各路径的传递特性。

2.2 驾驶员右耳声压响应贡献量分析

利用虚拟传递路径模型对驾驶员右耳声压38 Hz处峰值做分析，查找贡献量较大的传递路径，结果如图5所示。图中给出了贡献量较大的10条传递路径，路径编号见表2，X、Y、Z表示自由度。

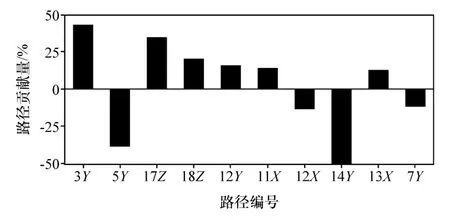
图5 驾驶员右耳声压路径贡献量C（38 Hz）

该10条路径对应的路径传递函数H（ω）和路径激励载荷F（ω）分别如图6和图7所示。

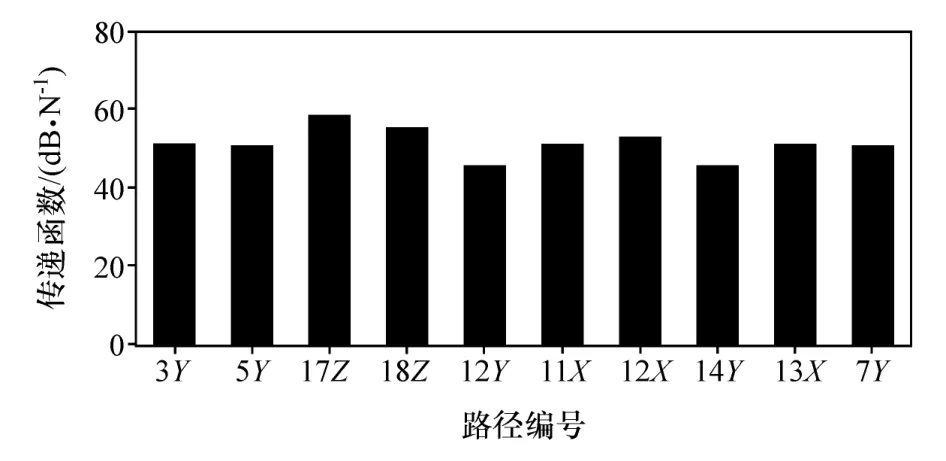
图6 路径传递函数H（ω）

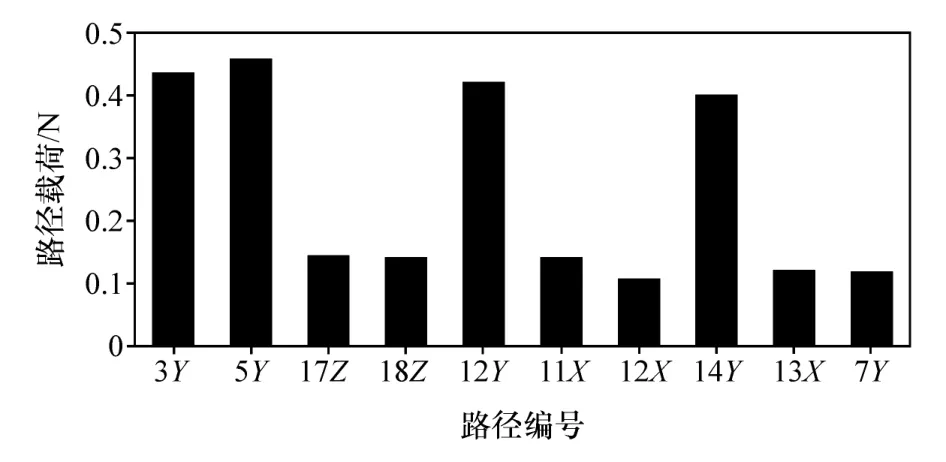
图7 路径激励载荷F（ω）

对驾驶员右耳声压响应贡献量最大的两条路径为左控制臂前安装点y方向（3Y）和右控制臂前安装点y方向（5Y），但这两条路径传递函数处于平均水平，而路径激励载荷明显高于其他路径，说明输入端载荷过大是造成这两条路径贡献量大的原因，可通过优化耦合处衬套刚度来减小载荷传递，从而控制车内响应。由于总响应是各路径响应的矢量和，某一路径响应改变后，总响应的幅值和相位都会发生改变。虽然路径5Y当前是负贡献，但当其他路径响应改变时，路径5Y较大的响应可能会使总响应与其夹角小于90°，从而成为正贡献，因此，优化时应当考虑右控制臂前安装衬套。

左、右后减振器安装点Z向（17Z、18Z）这两条路径，其路径传递函数高于其它路径，路径传递函数偏高是造成路径17Z、18Z贡献量大的原因，可优化车身结构以控制传递函数，从而控制噪声响应。为验证虚拟传递路径法查找问题的有效性，只优化减震器安装衬套刚度参数来控制车内噪声。

左下横臂安装点y方向（12Y）和右下横臂安装点y方向（14Y）的路径载荷同样高于其他路径，同时路径12X贡献量也较大，因此优化下横臂安装衬套X向和Y向刚度参数有利于降低驾驶员右耳噪声。

2.3 驾驶员座椅导轨振动响应贡献量分析

单位白噪声激励下，驾驶员座椅导轨Z向振动响应59 Hz处峰值的虚拟传递路径分析结果分别如图8～图10所示。

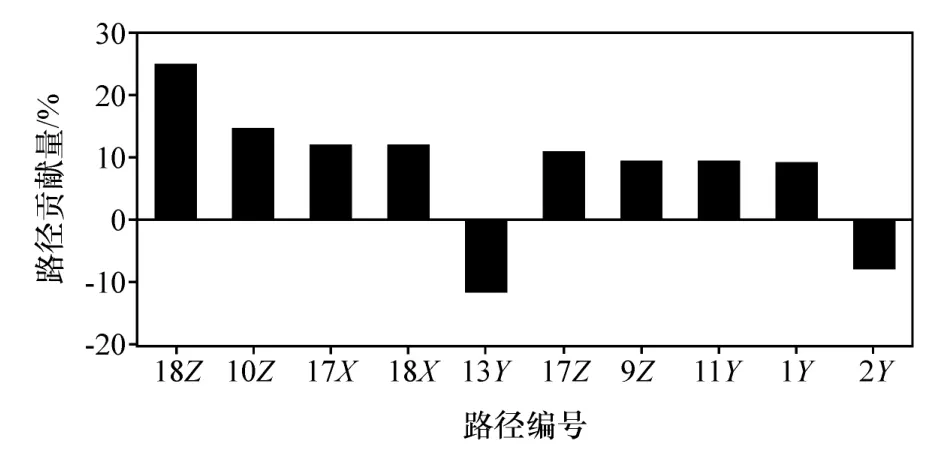
图8 驾驶员座椅导轨Z向振动路径贡献量C（59 Hz）

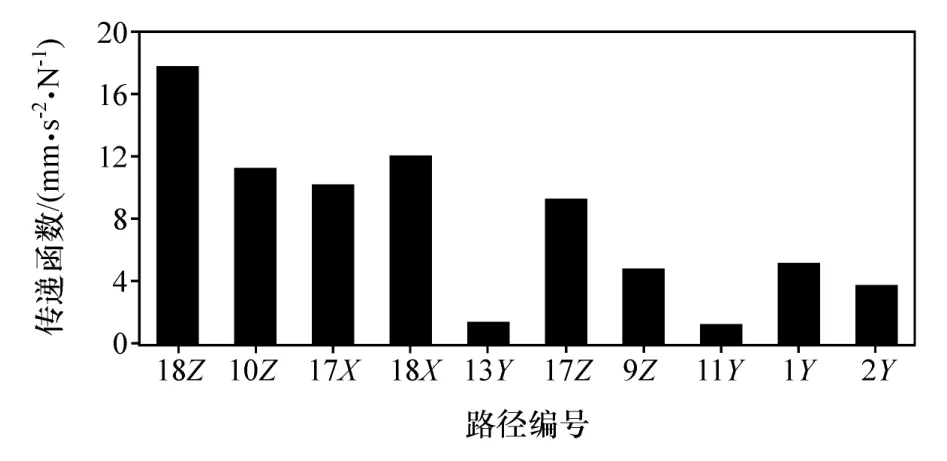
图9 路径传递函数H（ω）

对驾驶员座椅导轨贡献量较大的几条路径为后减振器Z向（17Z、18Z）、X向（17X、18X）和后纵臂Z向（9Z、10Z），路径传递函数偏高是造成路径贡献量较大的原因，可优化车身结构来优化路径传递函数，从而控制座椅的振动。与驾驶员右耳声压优化路径一样，只优化减振器衬套和纵臂安装衬套的刚度参数来验证虚拟TPA的有效性。

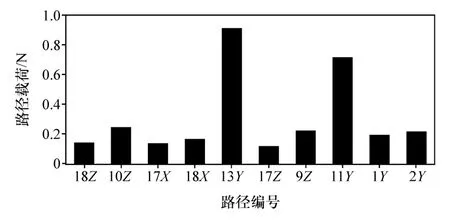
图10 路径激励载荷F（ω）

左上横臂安装点y方向（11Y）路径载荷高于其他路径，优化左上横臂的衬套刚度参数，有利于控制座椅振动。右上横臂安装点y向（13Y）贡献量同样较大，虽然该路径当前是负贡献，但与路径5Y分析一致，右上横臂安装衬套y向刚度同样需要优化。

综上所述，需要优化的衬套有：控制臂前安装衬套，减振器衬套，下横臂安装衬套，和上横臂安装衬套。通过优化衬套刚度参数，改变振动的传递特性来改善车内振动噪声响应。

3 优化改善

3.1 优化模型

根据以上分析，将需要优化的衬套刚度参数作为优化设计变量，如表3所示，衬套的原始刚度值作为优化初始值，选择刚度参数值上浮动30%、下浮动50%作为设计变量取值范围，以38 Hz处驾驶员右耳声压级与59 Hz处驾驶员座椅导轨Z向振动加速度的加权和最小为优化目标，建立如式（4）的优化模型。

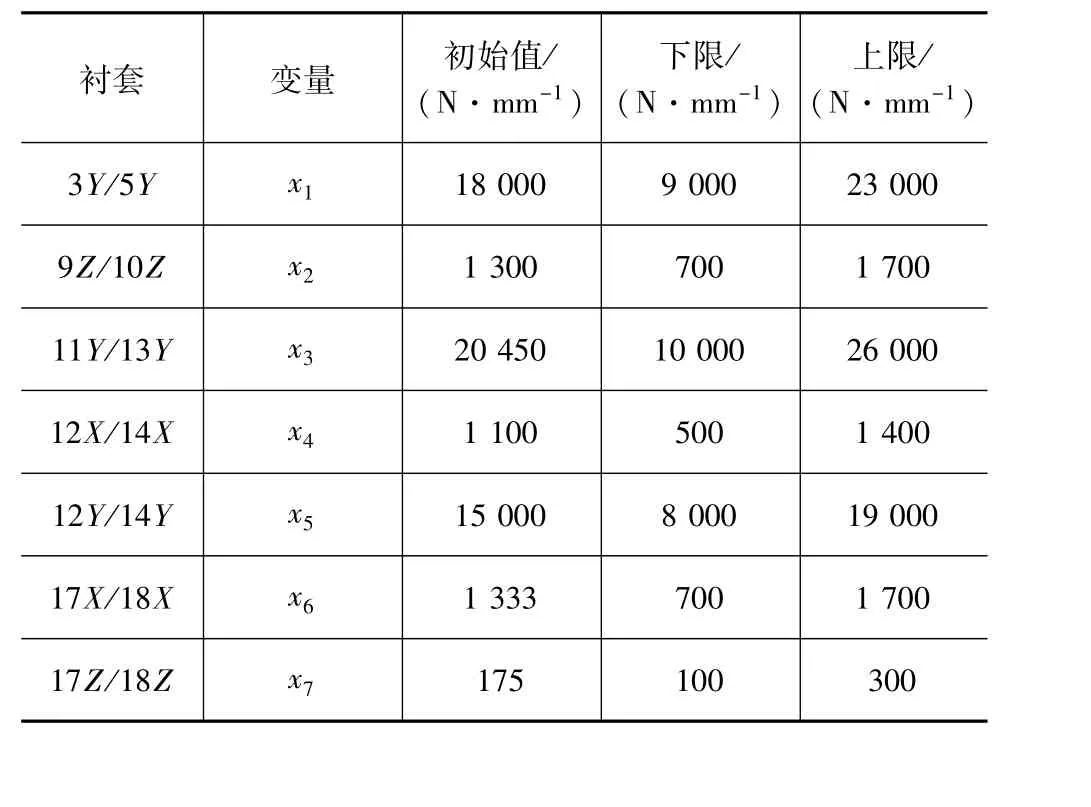
表3 优化变量

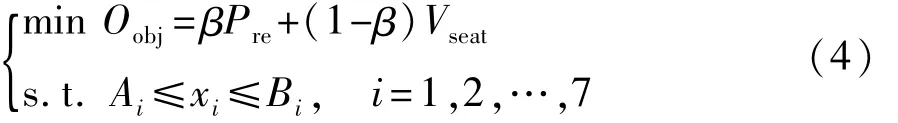
式中：Ai、Bi分别为第i个变量的取值下限与取值上限；Pre为驾驶员右耳38 Hz处的声压级值，dB；Vseat为驾驶员座椅导轨在59 Hz时的Z向振动加速度值，mm·s－2；β为权值，取 0.5。

在整车声— 固耦合模型基础上，建立优化模型，提交Optistruct计算，对各衬套刚度参数进行优化。

3.2 优化结果

衬套优化迭代历程见图11，经过4步迭代后结果收敛。各设计变量优化结果见表4。

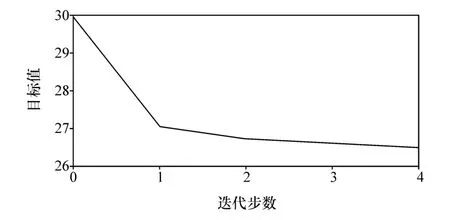
图11 优化迭代历程

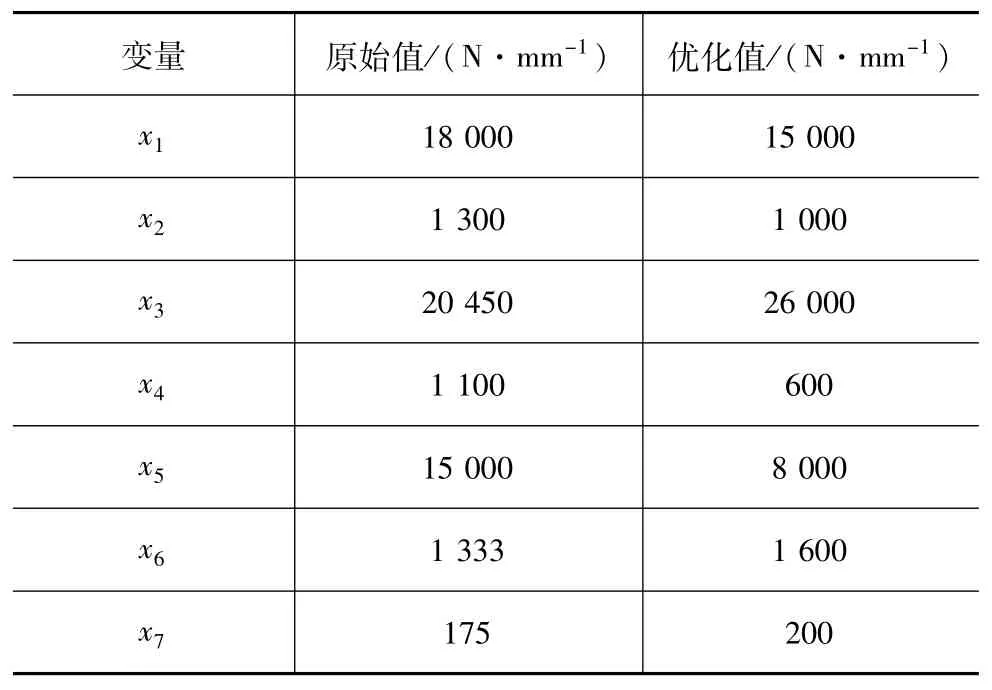
表4 设计变量优化结果

将优化后的衬套刚度参数值代入原整车声 固耦合模型中，并重新计算驾驶员右耳声压响应和驾驶员座椅导轨振动响应，优化前后对比结果如图12所示。

衬套刚度参数优化后，驾驶员右耳声压在38 Hz处减小2 dB，座椅振动在59 Hz处改善明显，说明衬套刚度参数的优化方案有效，即虚拟传递路径分析模型有效。同时，优化后的结果在某些频率处的峰值大于原始值，这是由于对衬套的优化方案都是针对驾驶员右耳38 Hz处和座椅振动59 Hz处的峰值响应，对其他频率处的峰值未作分析及优化，所以在其他频率处有可能出现大于原始值的情况。

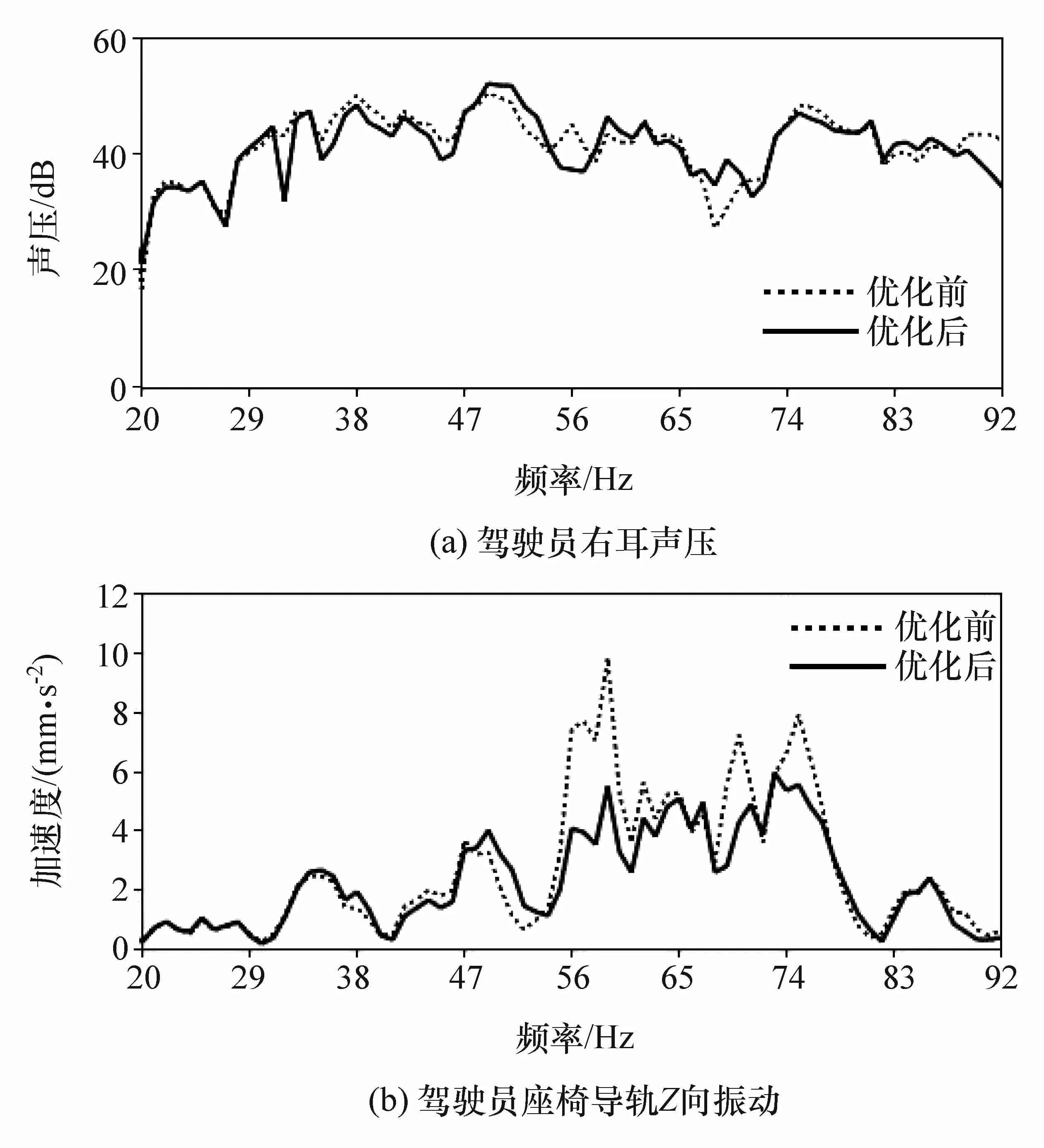
图12 衬套优化前后对比

4 结论

利用有限元方法建立整车NVH模型，并对车内声学振动响应进行预测，预测结果显示38 Hz处驾驶员右耳声压和59 Hz时的驾驶员座椅导轨Z向振动存在较大峰值。对响应峰值开展虚拟传递路径分析，根据分析结果，对贡献量较大的路径进行优化，优化后驾驶员右耳声压在38 Hz处减小2 dB，座椅振动在59 Hz处改善明显，表明虚拟传递路径分析法可查找车内振动噪声产生的原因，是整车开发初期诊断汽车NVH问题准确可行的方法。