车身壁板自由阻尼层稳健性优化设计*

苏仕见，徐元利，弓 剑，夏洪兵，胡海欧，霍俊焱

（1.天津科技大学机械工程学院，天津 300222； 2.天津市轻工与食品工程机械装备集成设计与在线监控重点实验室，天津 300222；3.中国汽车技术研究中心有限公司，天津 300300）

前言

随着汽车工业的发展，人们对汽车的驾乘舒适性要求越来越高，车内噪声是影响舒适性的重要因素，并已经成为评价汽车质量好坏的重要标准之一。

汽车运行时，车身薄壁板结构受到来自发动机和悬架等的激励后，产生振动并向车内辐射噪声。对产生噪声的薄壁板敷设阻尼材料能够起到显著的减振降噪的效果，因此，国内外学者在车身结构的附加阻尼层优化设计方面进行了大量的研究与应用［1］。黏弹性阻尼材料具有独特的力学特性，其参数损耗因子和弹性模量会随着频率和温度的变化而改变［2］，阻尼材料参数的温频依赖性往往会导致汽车NVH性能的不稳健问题。郑玲等［3］在车身声—固耦合模型中分析了车身各板件的声学贡献度，确定了对车身结构噪声贡献度最大的板件，并针对该壁板采用渐进优化算法进行了阻尼材料布局的拓扑优化。赵建轩等［4］采用Kriging近似模型与粒子群相结合的方法对阻尼材料的敷设厚度进行了优化，在保证汽车NVH性能不降低的情况下，阻尼材料取得了较好的轻量化效果。Balasubramanian等［5］通过计算车身板件的等效辐射声功率（equivalent radiated power，ERP）优化了阻尼材料的敷设位置。然而这些研究仅仅是对阻尼材料的布局或者厚度进行了确定性优化，并没有考虑阻尼材料的稳健性。阻尼材料的参数（损耗因子和弹性模量）具有统计分散性，传统的确定性优化可能会因为参数的不确定性因素而导致可行的设计不可靠甚至失效［6］。

本文中以等效辐射声功率（ERP）为优化目标，对车身壁板自由阻尼层布局进行拓扑优化；然后，考虑阻尼材料损耗因子和弹性模量的频率温度依赖性带来的车身结构噪声性能不稳健问题，结合蒙特卡罗模拟（monte carlo simulation，MCS）技术和序列二次规划算法（SQP），构造基于6σ稳健性的阻尼材料轻量化设计方法。

1 声—固耦合模型建立及NTF分析

1.1 声—固耦合理论

关于声— 固耦合问题，不仅要考虑车身结构的外部激励，还要考虑声压对结构振动的影响。将车身内部空腔离散化，可得空腔声场的波动方程为［7］

式中：Mf为声学等效质量矩阵；Cf为等效阻尼矩阵；Kf为声学等效刚度矩阵；R为结构与流体的耦合矩阵；·U·为节点加速度矩阵；p为节点声压矩阵。

不考虑空腔声压对车身结构振动作用时，结构振动控制方程为

式中：Ms为结构质量矩阵；Cs为结构阻尼矩阵；U为振动位移矩阵；Ks为结构刚度矩阵；Fs为结构的外部激励矩阵。

空腔声压对车身结构振动作用时，需要在空腔与车身壁板的耦合界面上添加压力载荷Ff，则振动控制方程为

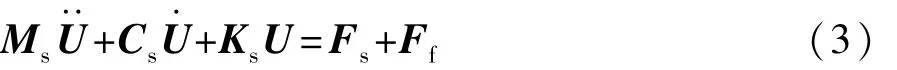
式中Ff为空腔声场对车身结构的作用力矩阵。

式（1）和式（3）描述了声—固耦合系统的动力学方程，由于Ff＝RTP，可以用统一的矩阵形式表示为

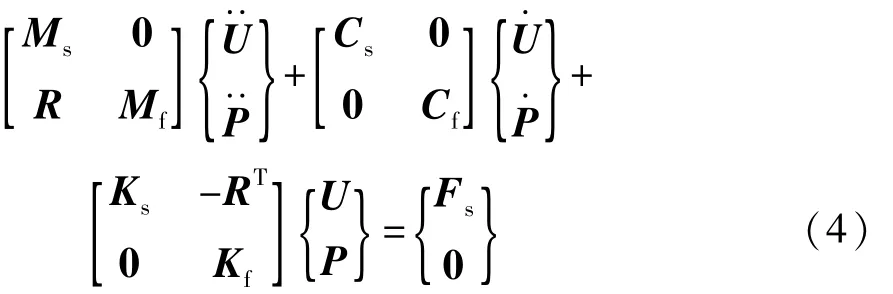
1.2 NTF理论

噪声传递函数（noise transfer function，NTF）是指在车身特定位置施加单向单位力的激励时，在车内引起噪声大小的敏感程度［8］，表示声腔与车身结构的固有特性。

噪声传递函数可表示为

式中：H（ω）为噪声传递函数；p（ω）为车内声压响应；Fs（ω）为结构激励力。

1.3 白车身有限元建模及模态分析

本文中以某型SUV为研究对象。采用壳单元建立白车身结构的有限元模型，单元基本尺寸为10 mm，在保证必要精度后对车身适当简化，忽略车身结构上较小的附件、倒角、小孔和凸台等。白车身有限元模型如图1所示，单元总数为717 931，节点总数为720 659，三角形单元占比为3.62%；车身结构焊点和粘胶采用RBE3单元模拟，螺栓连接采用RBE2刚性单元模拟；材料类型选择MAT1，其中弹性模量为 210 GPa，密度为 7 900 kg／m3，泊松比为0.3。在Optistruct软件中采用Lanczos算法计算出白车身结构的前6阶自由模态。

图1 白车身有限元模型

图2 白车身模态测试响应点

白车身模态试验采用激振器法，图2为测试响应点。进行模态试验时，将车身四角用空气弹簧支撑近似模拟自由状态的边界条件，然后将2个激振器分别安装在白车身右前纵梁和左后纵梁位置，激振器采用猝发信号对白车身进行激励，采集车身189个分组布置的加速度传感器振动响应信号，将采集到的响应信号在Test.lab系统中进行处理。仿真计算得到的各阶固有频率与试验测试值之间的对比如表1所示，各阶计算模态值与试验模态值之间的相对误差均低于5%，满足精度要求。

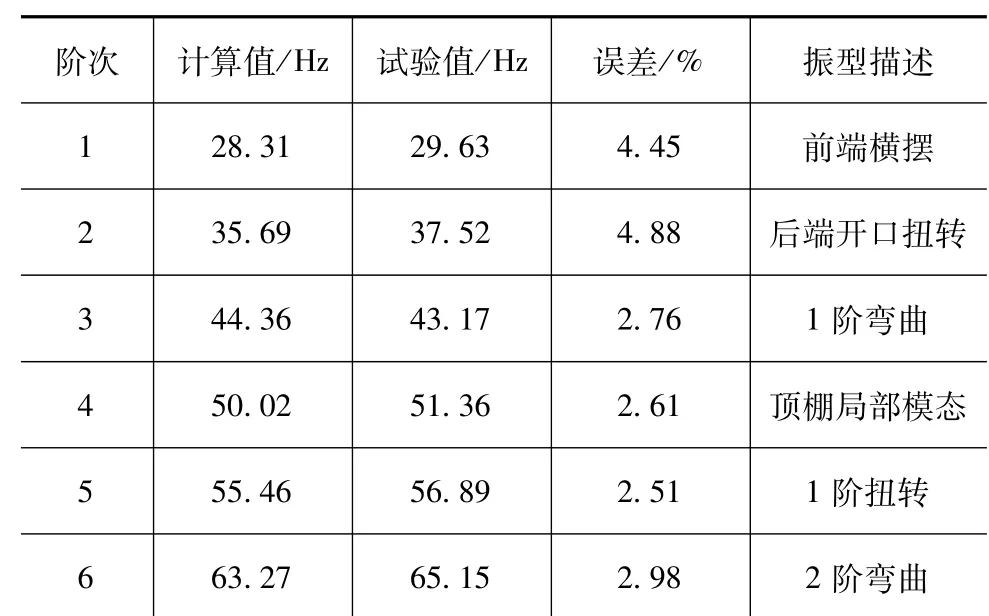
表1 计算模态值与试验模态值对比

1.4 声 —固耦合模型建立

在白车身模型的基础上，首先建立门盖系统、座椅系统、转向系统、副车架以及内外饰附件等有限元模型，并通过适当的连接方法将这些子系统模型与白车身连接起来构成内饰车身（trimmed body）模型；然后对内饰车身结构上的缝隙和小孔等进行适当的填补，使之形成一个封闭的结构模型；再将前后排座椅蒙皮划分为边长为30 mm的四边形单元；最后在内饰车身模型的内部抽取空腔。考虑到计算的效率和精度，采用单元长度为40 mm的标准划分声腔网格，得到192 566个四面体单元的声腔有限元模型，如图3所示。在Optistruct中通过设置ACMODL卡片可将内饰车身模型和声腔有限元模型耦合，建立声— 固耦合有限元模型，如图4所示。

图3 声腔有限元模型

图4 声—固耦合模型

1.5 NTF分析

噪声传递函数（NTF）分析主要考察动力总成系统和悬架系统与车身连接点的激励，其中发动机悬置有3个连接点，前后悬架共有12个连接点，排气吊耳有8个连接点，共计23个连接点。计算NTF时，分别在23个连接点的 X、Y和 Z方向上施加20～200 Hz的单位力载荷，选取驾驶员右耳位置节点为响应点。为更清楚地观察阻尼优化前后车身结构噪声性能整体的变化，分别将各连接点NTF的X、Y和Z方向结果用均方根（root mean square，RMS）曲线表示，分析结果如图5所示。

图5 所有连接点激励下NTF的均方根曲线

2 车身壁板自由阻尼层布局优化

2.1 ERP分析理论

车身板件振动会引起车内声压变动，等效辐射声功率（equivalent radiated power，ERP）可以评估板件振动与声压之间的关系［9］。ERP主要是通过计算车身板件的法向速度响应与单元面积的乘积，以评估特定激励下板件的最大可能辐射能量［10］，其表达式为

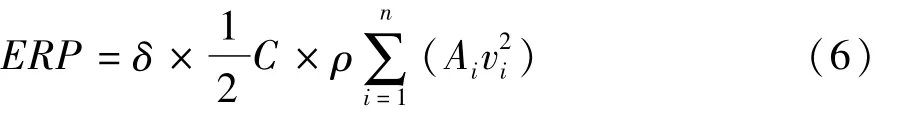
式中：δ为辐射损耗因子；C为声速；ρ为流体密度；Ai为单元面积；vi为单元法向速度。

式中：P为缩放因子（P＝1.0）；R为参考声压，R＝2×10－5Pa。

2.2 阻尼材料特性测试与分析

本文中涉及的自由阻尼层采用水性阻尼材料，其主要成分为高分子聚合物和无机填料。当水性阻尼材料与振动的车身壁板直接接触时，会将部分机械能转变成热能消耗掉，起到减振降噪的作用。阻尼材料通常以损耗因子来表征其阻尼性能。

水性阻尼材料属于黏弹性材料，其弹性模量和损耗因子与环境温度和频率密切相关。为进一步分析阻尼材料的特性，本文中参考GB／T 18258—2000阻尼性能测试方法，采用悬臂梁法测试阻尼材料参数；选取的水性自由阻尼层测试样本密度为803 kg／m3，泊松比为0.45，厚度为3 mm，测试结果如图6和图7所示。

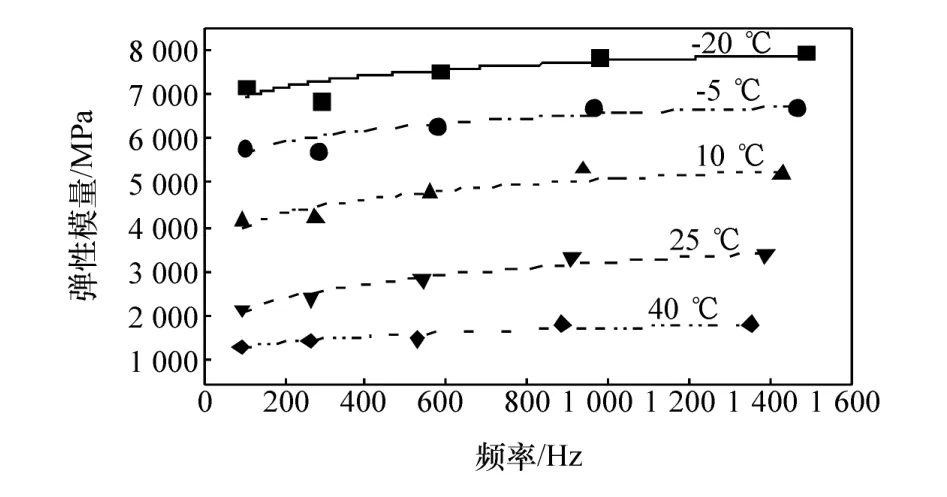
图6 阻尼材料弹性模量测试结果

2.3 车身壁板ERP计算与阻尼材料初始设计

在带有副车架的白车身动力总成系统和前后悬架系统的关键连接点X、Y和Z向同时施加20～200 Hz的单位激励（与NTF分析的激励点相同）；输出防火墙、前地板、后地板、左右后轮罩和顶棚等壁板件的ERP响应；在前面提及的壁板上敷设厚度为3 mm自由阻尼层，阻尼材料参数取温度25℃时的中值，即弹性模量为2 800 MPa，损耗因子为0.4，采用偏置的壳单元模拟，车身阻尼层初始设计如图8所示；计算敷设阻尼材料的白车身ERP，并对比阻尼优化前后白车身壁板ERP响应，如图9所示。

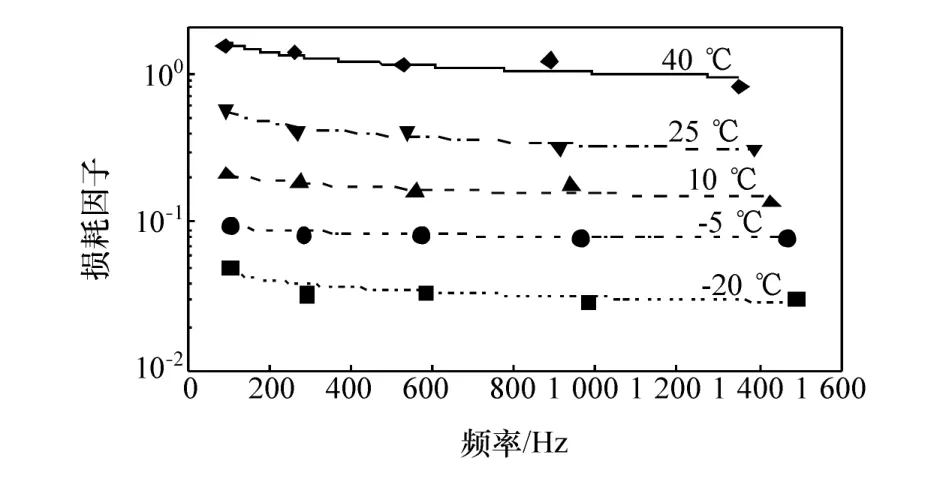
图7 阻尼材料损耗因子测试结果

图8 阻尼层初始设计示意图

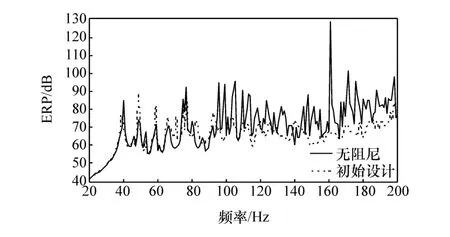
图9 阻尼材料敷设前后ERP对比

由图9可知，敷设阻尼层的白车身壁板ERP有明显的降低，然而按这种方式敷设的阻尼材料质量为14.51 kg，大大增加了汽车的整体质量，故有必要对该初始设计的阻尼材料布局进行拓扑优化，以实现轻量化的目标。

2.4 基于ERP的自由阻尼层拓扑优化

2.4.1 拓扑优化模型

以阻尼材料的质量最小为优化目标，20～200 Hz频率范围的白车身壁板ERP响应小于90 dB为约束条件，建立拓扑优化数学模型：

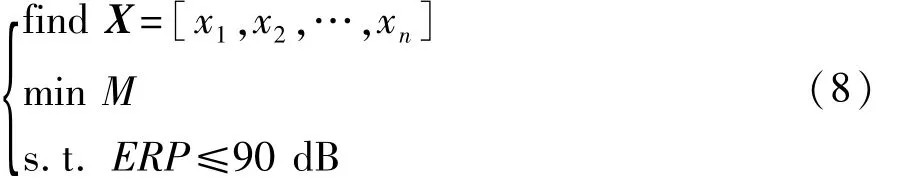
式中：X为设计变量；M为阻尼材料的总质量。

2.4.2 拓扑优化结果及分析

采用上述拓扑优化模型对白车身壁板阻尼层的布局进行优化，获得拓扑优化云图，如图10所示。图中深色区域表明该区域的ERP贡献量较大，需要提高阻尼材料的单元密度，以此为阻尼层的精确布局提供参考。

图10 拓扑优化云图

根据拓扑优化云图和水性阻尼材料的制造工艺，设计的白车身阻尼层布局如图11所示。计算阻尼层拓扑优化后的白车身ERP，并对比优化前后的ERP结果，如图12所示。拓扑优化后的白车身ERP响应在考察频段内均小于90 dB，满足优化约束条件要求。拓扑优化后阻尼材料的总质量由初始设计方案的14.51减少至5.61 kg，取得了较好的轻量化效果。将拓扑优化前后的阻尼材料分别带入声—固耦合模型中，并计算车身所有连接点激励下的驾驶员右耳响应点NTF均方根曲线，如图13所示。由图可知阻尼拓扑优化后NTF响应在某些频率下略有升高，但整体水平与初始设计方案接近。

图11 阻尼层拓扑优化结果

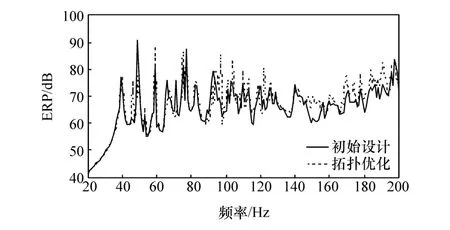
图12 阻尼层拓扑优化前后ERP对比

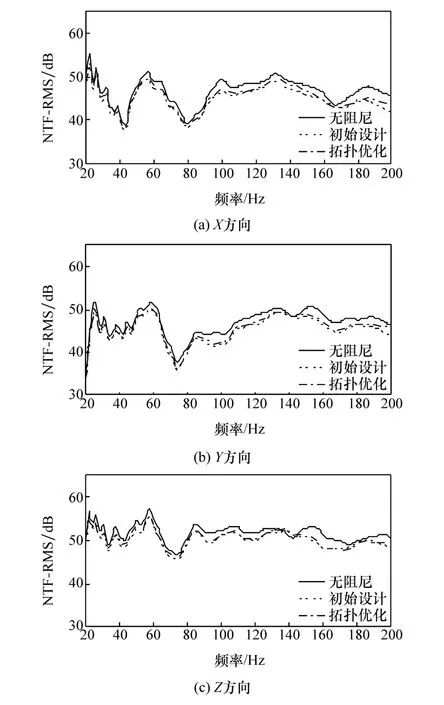
图13 阻尼层拓扑优化前后的NTF均方根曲线对比

3 基于6σ的车身自由阻尼层稳健性优化

6σ稳健性优化与传统的确定性优化相比不仅优化了设计目标，而且能降低约束条件和目标响应对设计变量变化的敏感性，即提高了结构的稳健性［11］。一般而言，6σ稳健性优化设计将使阻尼材料的减振降噪性能在规定的范围内变动，不会因频率和温度等因素的变化而影响到车内噪声的质量水平。阻尼材料稳健性优化设计流程简图如图14所示。

3.1 稳健性优化模型

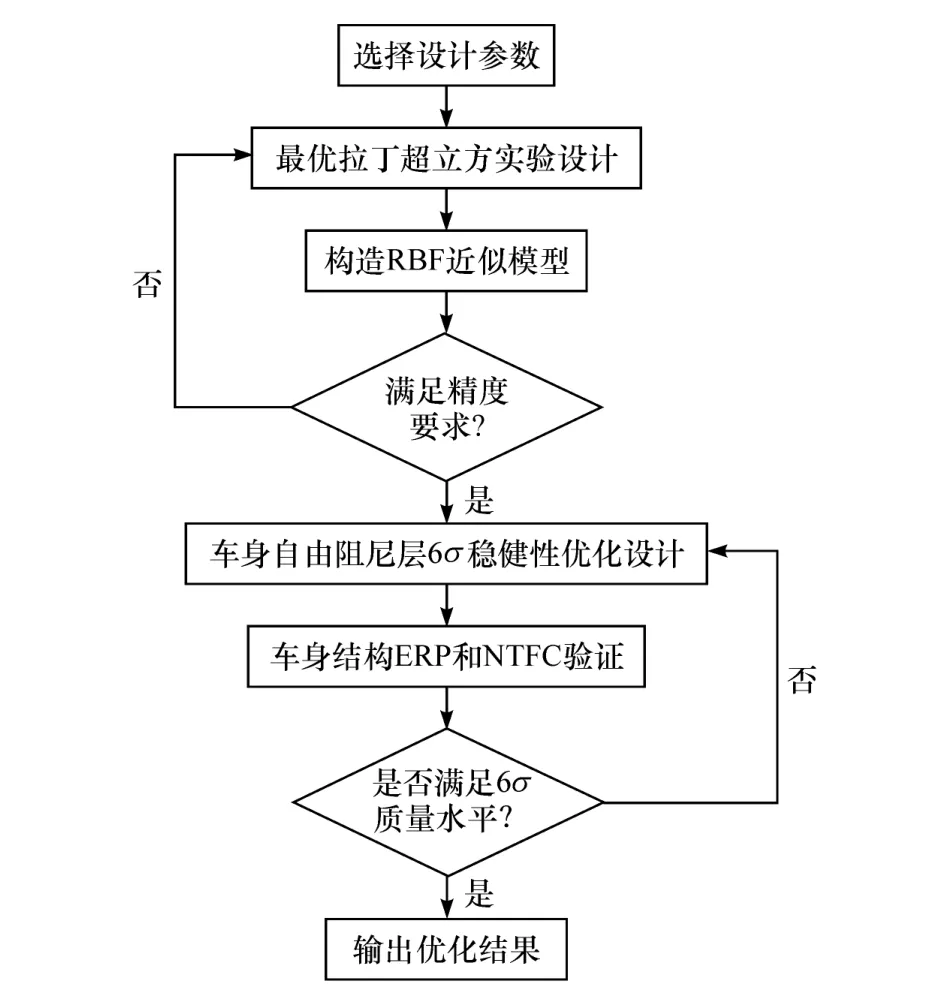
图14 稳健性优化设计流程图

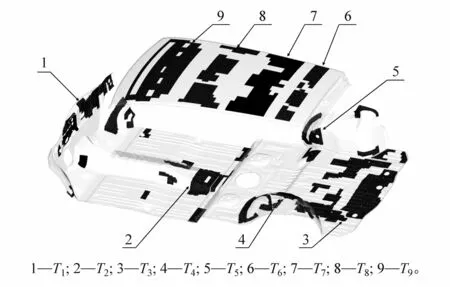
图15 设计变量分布区域示意图

本文中将拓扑优化设计的车身阻尼材料按照防火墙、前地板、后地板、左右后轮罩和顶棚等位置划分为9个区域，如图15所示；选取这9个区域阻尼层的厚度T1，T2，…，T9为设计变量，同时考虑阻尼层厚度分布特性、阻尼材料弹性模量E和损耗因子η不确定因素干扰的影响，并以此作为稳健性优化的随机变量；设定 E、η和Ti（i＝1～9）的分布特性为正态分布，E和 η的变异系数为 0.03，Ti（i＝1～9）的变异系数为0.01，设计变量取值范围如表2所示。为了后面更加直观地分析优化前后车身壁板ERP整体的变化效果，将20～200 Hz频段内的ERP曲线换算成ERP均方根；本研究以ERP均方根为约束，阻尼层总质量最小化为目标，对阻尼材料进行6σ稳健性优化设计。6σ稳健性优化模型为

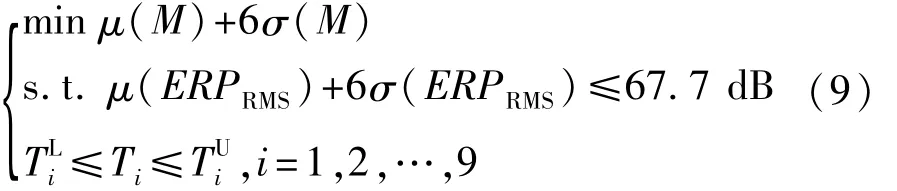
3.2 近似模型构建

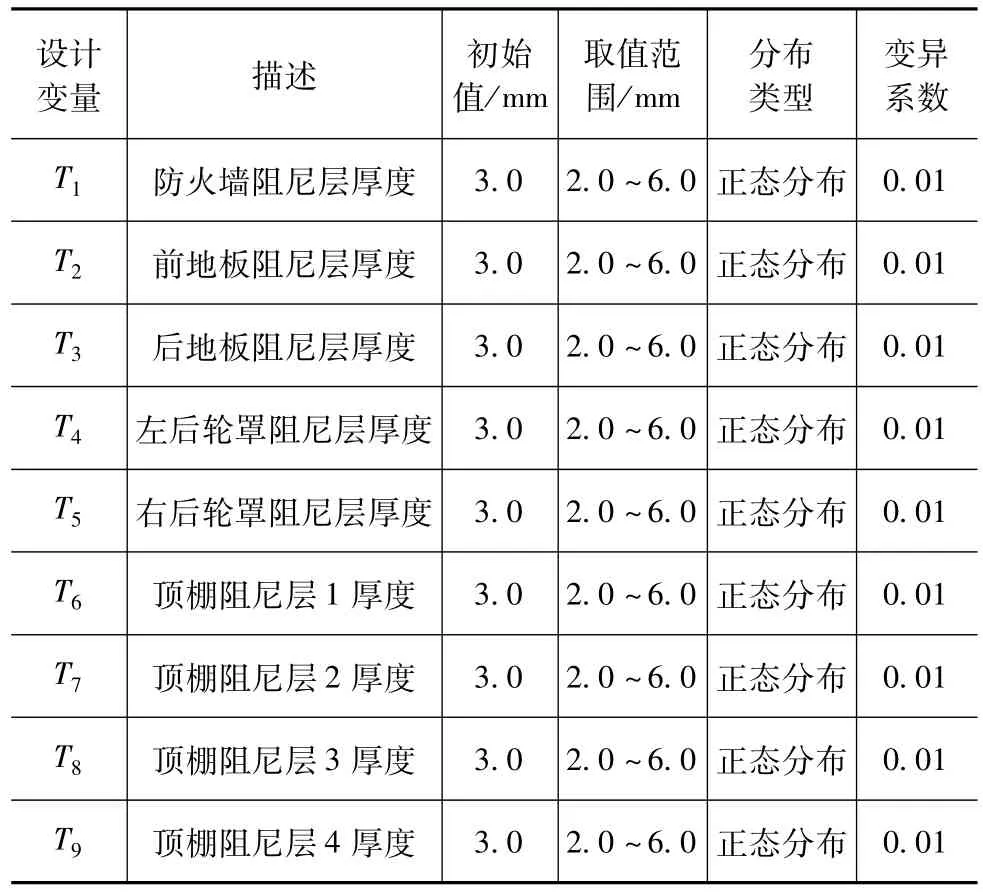
表2 设计变量

本文中使用径向基函数（radial basis function，RBF）近似模型来代替有限元模型计算，以提高计算效率。RBF是由Powell提出的一种多维空间插值技术，具有结构简单、收敛速度快的特点，能够逼近任意的非线性函数［12］，其解析表达式为

式中：φK（rK）为基函数；λK为样本点的加权系数；rK（X）＝‖X－XK‖为X与第K个样本点在设计空间的欧氏距离。

采用最优拉丁超立方实验设计对9个设计变量和3个随机变量在定义域内进行采样，采样次数195次；将各组采样值带入白车身有限元模型进行计算，得到车身壁板ERP和阻尼层质量的响应值；构建设计变量、随机变量与约束目标响应的RBF近似模型。用RBF模型代替有限元模型进行优化计算时需要对近似模型的精度进行评估，评价指标包括相对均方根误差RMSE和决定系数R2，其表达式分别为

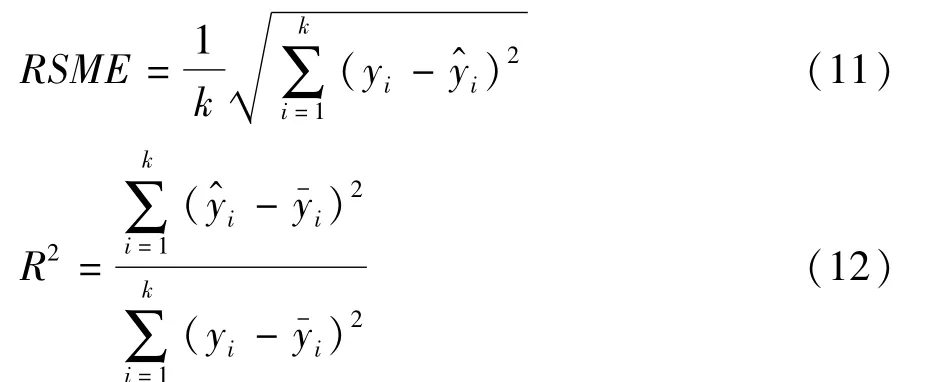
式中：k为测试点个数；yi为真实响应值；为真实响应的均值为由近似模型得到的预测值。

RMSE和R2表示真实值与响应面之间的差异程度。RMSE值越小表示响应面的拟合精度越高；R2值越接近1时表示近似模型的精度越高。采用最优拉丁超立方抽取15个样本点，对RBF近似模型进行验证，结果如表3所示。2个响应的RMSE均小于0.1，R2均大于0.9，说明建立的RBF模型精度较高，满足优化计算要求。

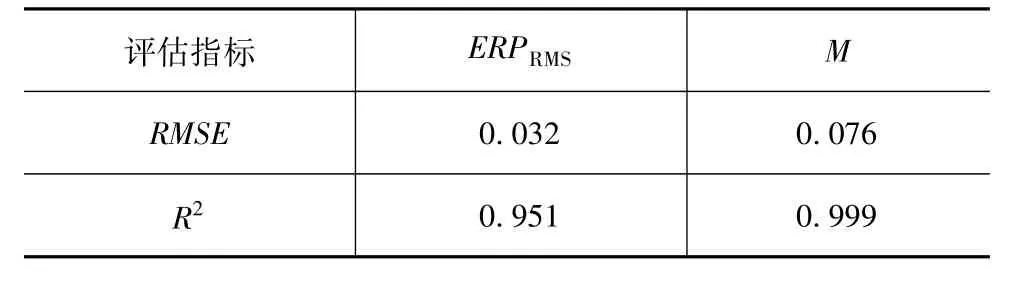
表3 RBF近似模型精度评估表

3.3 拓扑优化方案稳健性分析

车身壁板阻尼层的拓扑优化设计方案，当阻尼材料参数（损耗因子和弹性模量）因频率和温度变化发生扰动时，将导致车身NVH性能的波动，从而产生不可预料的车内噪声。因此有必要进行6σ稳健性分析，评估该方案的质量水平和可靠性。

6σ稳健性分析的目的是评价阻尼层拓扑优化方案的质量水平，是稳健性优化的基础。本文中采用蒙特卡洛模拟（MCS）分析拓扑优化方案的质量水平，选取阻尼材料的弹性模量E、损耗因子η和阻尼层厚度Ti（i＝1～9）分布特性作为随机变量，并根据对应的变异系数定义其标准差。基于前面建立的RBF近似模型，采用简单随机采样方法采集样本点，采样次数为1 000次，得到拓扑优化方案的概率分布特征、质量水平和可靠度，如表4第2、3、4列所示。分析结果显示ERP均方根没有达到6σ质量水平，且可靠度仅为58.26%。

3.4 6σ稳健性优化设计及结果分析

6σ稳健性优化采用双循环优化方法，即将稳健性分析过程内嵌于确定性的优化设计中。本文中在3.3节的6σ稳健性分析基础上，采用SQP算法进行阻尼材料的稳健性优化，优化结果如表4第5、6、7列所示。

拓扑优化方案ERP均方根的均值为67.7 dB，标准差为2.91，可靠度为58.26%；6σ稳健性优化后ERP均方根的均值为67.2 dB，标准差为0.86，质量水平达到6σ水平，可靠度达到99.99%，优化前后ERP均方根分布情况如图16所示。通过6σ稳健性优化设计，阻尼材料总质量为7.19 kg，比拓扑优化设计方案（5.61 kg）增加1.58 kg，但仍比初始方案（14.51 kg）减小 7.32 kg。

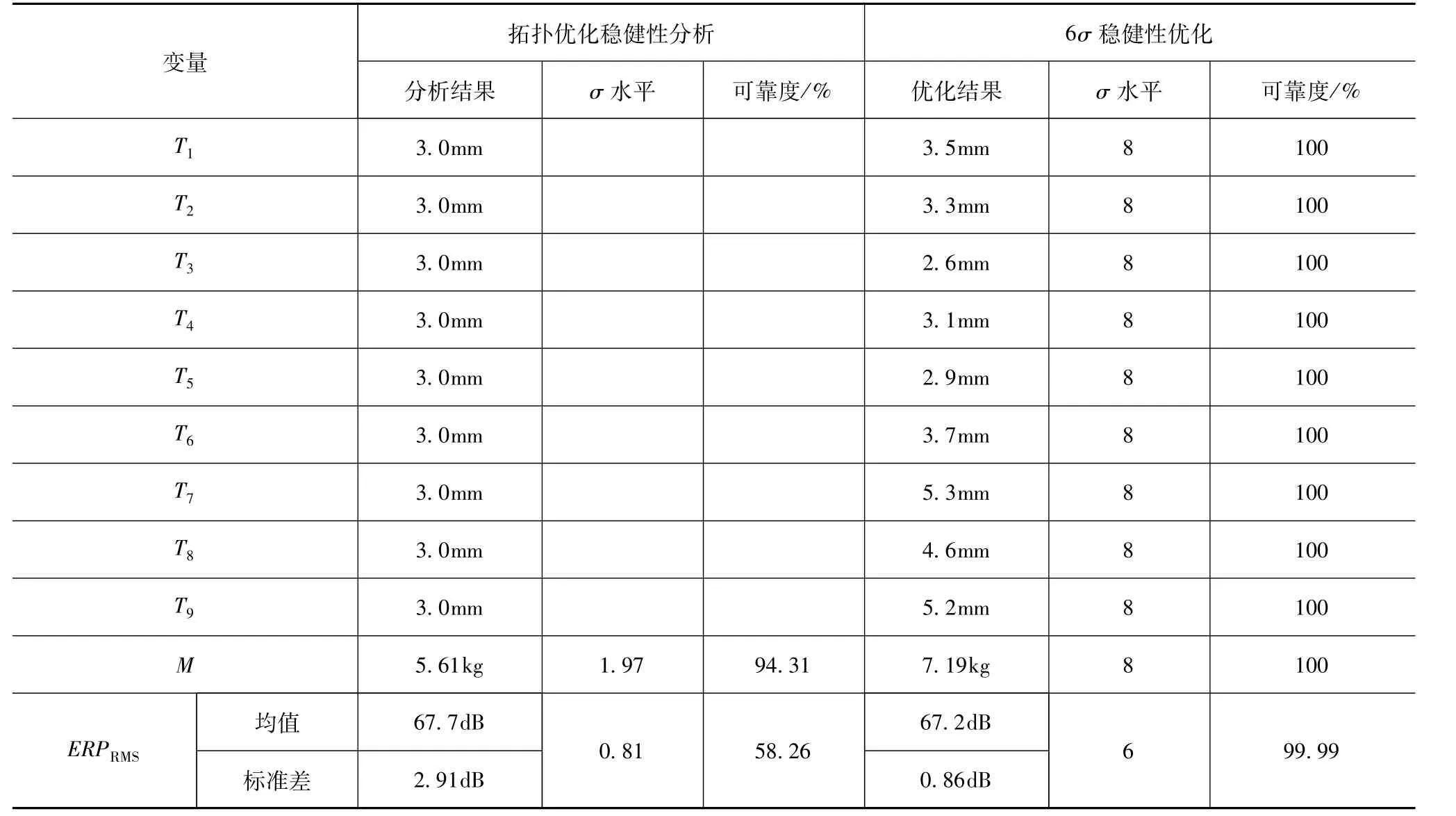
表4 拓扑优化与6σ稳健性优化结果

将阻尼材料稳健性优化结果带入声 固耦合有限元模型，得到优化前后所有连接点激励下的驾驶员右耳位置NTF均方根曲线，如图17所示。阻尼材料拓扑优化方案和稳健性优化方案与初始设计方案相比，NTF均方根曲线基本一致，没有出现明显的峰值，表明优化方案可行。

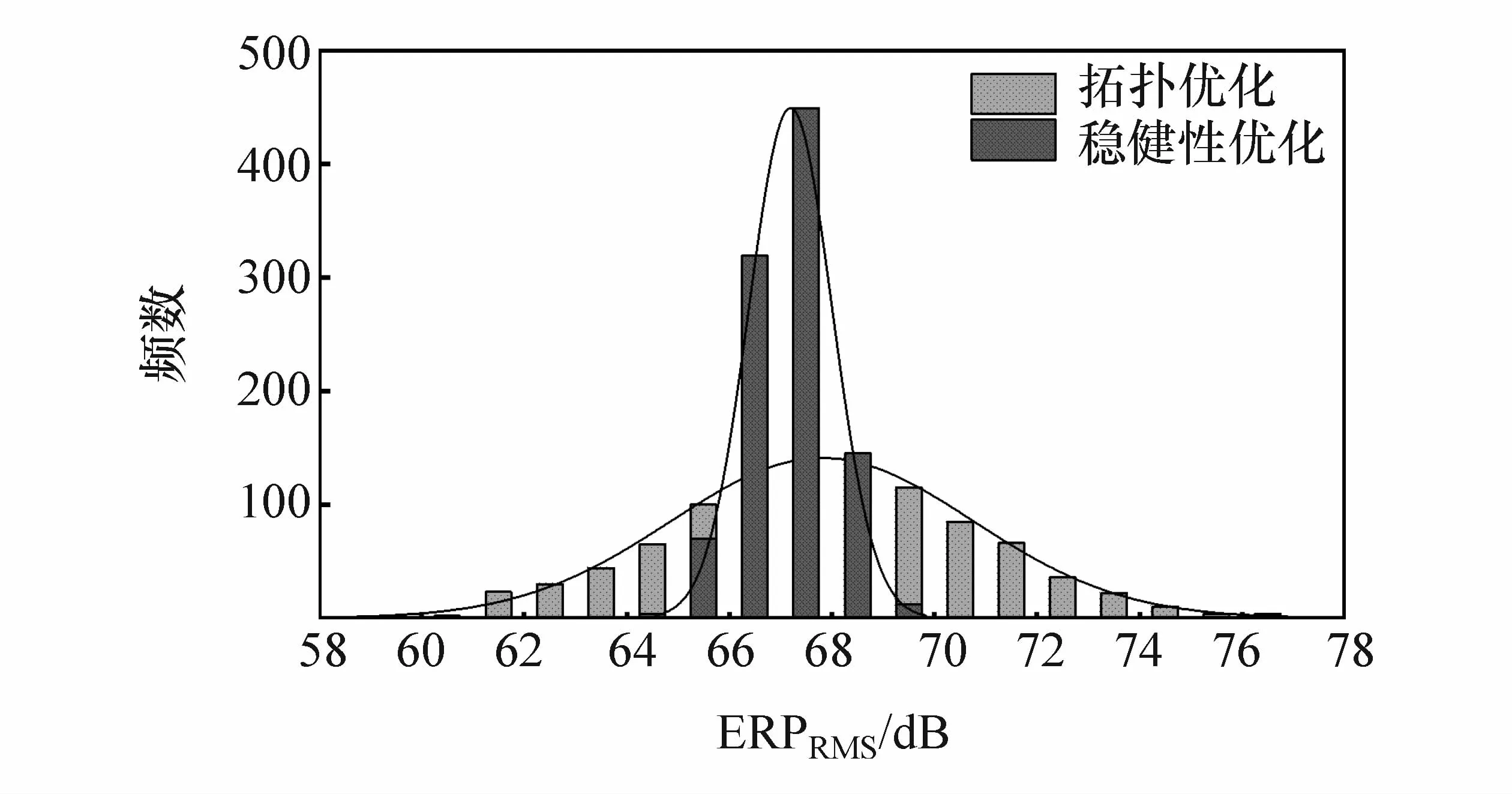
图16 拓扑优化与6σ稳健性优化的ERP均方根分布图

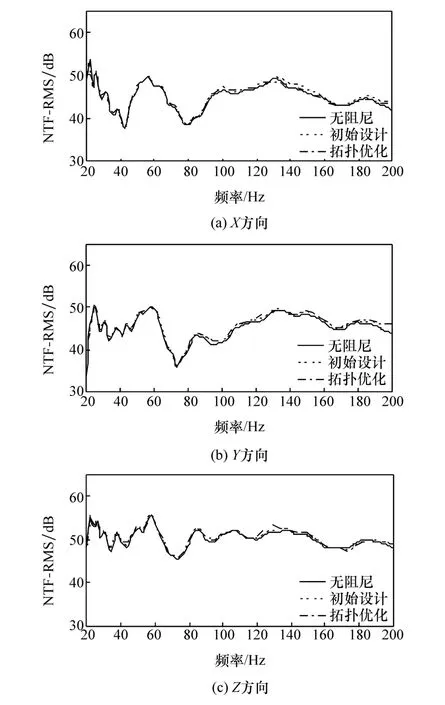
图17 阻尼层不同设计方案的NTF均方根曲线对比

4 结论

（1）在白车身有限元模型上建立阻尼层单元，以车身壁板ERP为优化目标对阻尼层布局进行拓扑优化，优化后阻尼材料总质量比初始设计方案减少了61.34%；将优化方案带入声 固耦合模型中，获得车身关键连接点激励下的驾驶员右耳位置NTF均方根曲线，与初始设计方案相比基本相当，且较没有敷设阻尼层的车身结构取得了显著的降噪效果。

（2）考虑阻尼材料参数（损耗因子和弹性模量）以及阻尼层厚度分布特性的不确定因素，对拓扑优化方案进行了6σ稳健性分析，结果显示车身壁板的ERP均方根没有达到6σ质量水平，可靠度仅为58.26%。

（3）针对拓扑优化方案的稳健性分析结果，以阻尼层的厚度为设计变量，损耗因子、弹性模量和阻尼厚度分布特性为随机变量，采用蒙特卡洛模拟和序列二次规划算法进行6σ稳健性优化；优化后ERP均方根的均值由67.7降低至67.2dB，标准差由2.91减小到0.86，可靠度达到了99.99%，阻尼材料总质量比初始设计方案减少了50.45%，效果显著。该优化设计方法为汽车的NVH性能稳健性和轻量化设计提供了参考，具有一定的理论和工程实际意义。