基于数学史的探究性学习案例*——“数系的扩充”教学设计

封志红

(江苏省泰兴中学，225400)

一、教学目标

知识技能 (1)了解数系发展历史和数集的扩展过程;(2) 理解复数的有关概念以及符号表示.

过程与方法 经历数系的扩充过程,体验复数引入的必要,探究复数相等的概念,领悟类比的思想方法.

情感与态度 在问题情境中了解数系的扩充过程,体会实际需求;由数系的扩充过程,感受人类理性思维的作用以及数与现实世界的联系.

二、教学重点和难点

重点 对引入复数的必要性的认识,理解复数的基本概念.

难点 虚数单位i的引入以及复数概念的生成.

三、教学流程与设计意图

1. 设置情境,再现历史

问题1 将10分成两部分,使两者的乘积为40.

设计意图 一方面展示数学家卡当的风采,激发学生的学习兴趣;另一方面,引领学生重温历史,感悟数学发现并不神秘,数学家也是从常规问题入手的.

问题2 有没有两数之和为10且积为40呢?那为什么刚才的问题无解呢?

设计意图 充分暴露数学家的思维过程.一方面让学生体验数学家的科研精神；另

一方面让学生处于“愤悱”状态.

问题3 实数集中有没有这样的两个数?

设计意图 打破原有认知平衡,形成认知冲突,让学生感受到原有的数已经不够用了,体现学习新知识的必要性.

2. 设计问题,追溯历史

问题4 数集经历了哪几次扩充?

设计意图 学生已经学习过自然数、整数、分数、负数、有理数、无理数、实数等.在此基础上,帮助学生重新建构数集的扩充过程,即自然数集→整数集→有理数集→实数集.这是学生的“最近发展区”,也是本节课知识的生长点.

问题5 数集的每一次扩充分别解决了哪些问题?

计意意图 学生通过小组合作交流、回忆、思考每次数集扩充的必要性,解决了哪些问题,即数集为什么要扩充?通过板书:

让学生感受到这些数的产生不是从天而降,既是数学内部发展的需要,也是社会发展

的需要.

问题6 这几次扩充有什么共同的特点?

设计意图 一方面培养学生的观察、概括与表达能力;另一方面通过对前几次数集扩充的梳理,为数系的再一次扩充以及如何扩充打好坚实的基础.让学生感受到数系扩充的合理性,并能提炼出数系扩充的一般原则.由此,突破本节课的一个难点.

3. 借鉴历史,生成理论

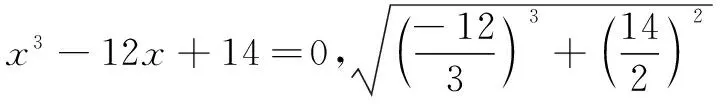
设计意图 引领学生再现卡当问题,将问题转化为找一个数的平方为-1,而且运用规范醒目的板书和留白艺术,给予学生充分思考问题的时间与空间,从而让“引入新数”水到渠成.

T: 为什么用i呢?

i是“虚幻的”英文单词imaginary的第一个字母.

T: 是谁引入了i呢?

卡当只是发现了这个矛盾,它的引入者是被称为“分析的化身”的瑞士著名数学家欧拉,引入时间公元1777年.从十六世纪到十八世纪,历史的车轮已经行进了两百多年,可见科学上每一步的迈出是多么的艰辛!而这一年又是与虚数单位i结下不解之缘的高斯诞辰之年.数学的历史充满了不少巧合.

设计意图 教师通过自问自答,介绍与虚数单位i有关的历史,激发学生兴趣,强化对i的认识,并让学生感受到科学上每一步的迈出是多么的艰辛!

问题7 引入i后,你能写出卡当要找的数吗?

问题8 你还能写出其他含有i的数吗?

设计意图 学生利用新知解决卡当问题,通过举例,加深对i的理解,为复数代数形式的建构奠定基础.

问题9 你能写出一个形式,把刚才所写出来的数都包含在内吗?

设计意图 数学需要形式化、符号化.复数的代数形式正是这一体现,也是本节课的重点与难点.笔者通过设计问题7、8的铺垫,对问题9的提出,引导学生由特殊到一般,抽象概括出复数的代数形式,培养学生抽象概括能力.

问题10a+bi(a,b∈R)一定是虚数吗？

设计意图 引导学生自然而然地想到要对复数进行分类,从而深化对复数概念的理解,攻克本节课的重点.

4. 精选例题,学以致用

例1 请你说出下列集合之间的关系:N,Z,Q,R,C.

例2 写出下列复数的实部与虚部,并指出哪些是实数,哪些是虚数,哪些是纯虚数.

例3 实数m取什么值时,复数z=m(m-1)+(m-1)i是

(1)实数？(2)虚数？(3)纯虚数？

问题11 对于复数z1=a+bi,z2=c+di(a,b,c,d∈R)在什么情况下相等呢?

例4 已知(x+y)+(x-2y)i=(2x-5)+(3x+y)i,求实数x,y的值.

设计意图 例1主要是前后呼应,采用概念同化的方式完善认知结构;例2、例3主要是巩固复数的分类标准;例题4主要是强化复数相等的充要条件，让学生在解决问题的过程中内化复数有关概念,起到及时反馈、学以致用的功效.

5. 反思总结,提炼收获

T:回顾本节课,你有哪些收获呢?

回顾本节课,i的引入者是欧拉,问题的提出者是卡当.卡当虽然没有解决问题,但他依然是大数学家,因为,发现问题比解决问题更重要.哈尔莫斯说,问题是数学的心脏.

会不会还有复数以外的数呢?数学是无穷的科学,正如这无边无际的海洋.我们就是这一叶扁舟,在知识的海洋探索永无止境,正如屈原所说“路漫漫其修远兮,吾将上下而求索.”以此和大家共勉.

(投影:问题是数学的心脏.数学是无穷的科学.路漫漫其修远兮,吾将上下而求索.)

设计意图 通过学生总结、教师提炼,深化内容,让学生体会数系扩充过程中蕴含的创新精神和实践能力,感受人类理性思维的作用以及数与现实世界的联系.最后,以三句名言作为结束语,期望与学生产生共鸣.