“以讲促思”在高三数学复习中的应用研究
李素文
(江苏省南京市六合区程桥高级中学,211504)
在高三数学复习中,利用学生讲题、说题,暴露学生的真实思维过程,知识建构,引起其他学生的共鸣,冲突,从而内化知识,收获思想,领悟方法,掌握解决问题的策略,真正提高高三数学复习的有效性和高效性.笔者在高三数学教学实践中,利用学生讲题促进学生的反思能力,并且使得“学生学会学习”,有效地提高了学生的数学素养和学业成绩,取得了较好的效果.
一、激活思维火花,提升解题反思能力
现代数学教学论认为:数学思维训练应由习惯性思维走向反思性思维,只有让学生通过对自己的数学活动过程进行不断地反省、概括和反思,有意义地纳入、重组和改造,才能实现新知识与原有认知结构的相互结合,建构新的认知结构.高三数学复习中的测试、练习很多.在诸多的练习中,会出现很多的错题,暴露学生解题中知识、方法、过程中存在的问题.这些知识如果依赖教师的讲解,会事倍功半.高三学生已有一定的知识储备,掌握了基本的解题方法和数学思想.让学生自己去讲题,可以发挥学生的主体地位,给学生展示自己的舞台,激活学生思维的火花.在生生、师生的思维冲突中,加深对问题的理解,寻找数学本质,提高学生的解题能力.
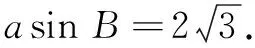
(1)求角A的大小;(2)若D为BC的中点,求线段AD的长.
生1:第(1)问利用正弦定理,直接求解,具体过程如下:
第(2)问利用余弦定理,具体过程如下:
在∆ABC中,由余弦定理,得
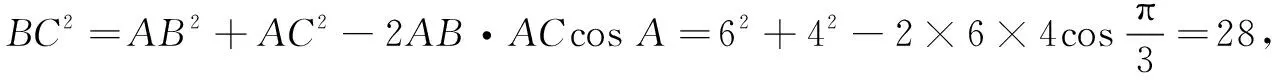
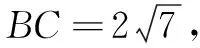
由余弦定理,得
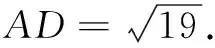
师:(总结)本道题是一道中档题,考查正余弦定理的应用,在解三角形的题目时要注意应用两个定理;另外,注意格式的规范性,公式的呈现一定要有.大家还有没有其他的解法?
生2:第(1)问还可以利用三角形的面积公式,过程如下:
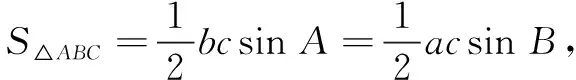
师:很好,两位同学从两个角度解决此题目,说明大家能够对两个公式灵活运用.第(2)问有没有其它的方法呢?
生3:(运用坐标法)以AB边所在的直线为x轴,建立如图1所示的直角坐标系,则
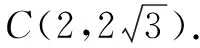
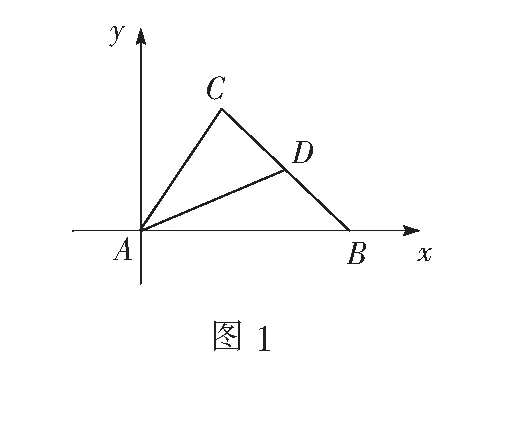


师:非常好,运用解析几何知识,建立坐标系,转化为两点间距离公式.求线段长还可以运用什么知识呢?
生5:(平行四边形法则与余弦定理结合)
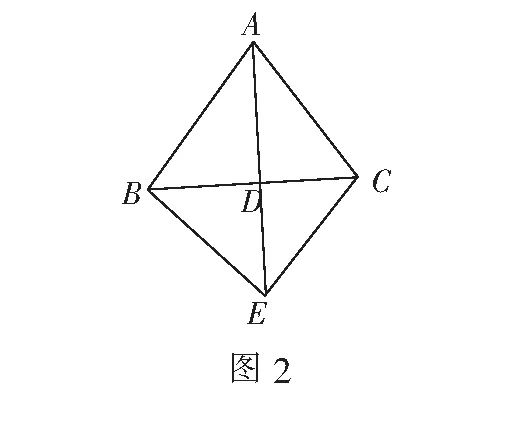
以AB,AC为邻边作平行四边形ABEC(如图2).
在∆ABE中,有
AE2=AB2+BE2-2AB·BEcos∠ABE
=62+42-2×6×4cos 120°=76,
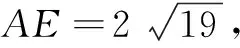
师:这道题形式给出的是解三角形,同学们不但练习了解三角形,还能与其它知识融会贯通,做得很好.高三复习就应该这样,积极寻求解题的多种途径,反思相关的知识,才能对问题有更深层次的理解,从而拓宽我们的发散性思维,提高应变能力,增强创新意识和积极探索问题的能力.
高三一轮复习中,学生的错题、相似题、经过学生讨论能够解决的较难题等都可以作为讲题的素材,让学生去讲题.这样不但提高了学生学习数学的积极性和主动性,而且提高了学生的解题能力和思维品质,同时提高了学生的信心和成就感.乔治·波利亚说过:“数学问题的解决仅仅只是一半,更重要的是解题之后的回顾.”因而,学生讲完题目后,教师还要留点时间给学生整理,还可以让讲解人把整理好的题目张贴在墙报上,让学生反思总结,发现规律,形成技能技巧.
二、凝聚集体智慧,利用微专题,提高复习的有效性
微专题教学,强调微而不小、强调以生为本、强调见微知著,可以更有针对性、时效性、灵活性.因而微专题教学在高三数学复习中很受欢迎.根据本班学情,让学生通过小组合作去完成一个微专题.首先,在平时的练习中寻找大部分学生的易错点,明确具体知识点,然后将专题内容发给小组,在教师的指导下,组长再细分知识点分配给组员,由组员选题,后续并负责讲此题,最后组长汇总整理成专题交给教师再次审核,通过后再面对全班讲解,对于有些选题不当的再次调整.专题讲过之后,全班整理此专题到笔记本,然后再次反思完善.通过高三一年的实践,同学们整理了分段函数、对数函数、平面向量的数量积、求离心率、隐形圆等微专题.通过这些专题的整理,不但提高了学生的总结能力,还对这些题有了系统的认识,从而提高了学生的反思能力.下面给出学生整理的微专题——分段函数.
案例2 微专题——分段函数
(1)周期性、奇偶性、单调性
生1 设f(x)是定义在R上且周期为2的函数,在区间[-1,1]上,
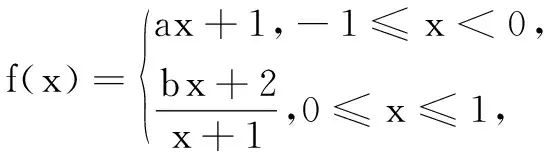
生2 已知
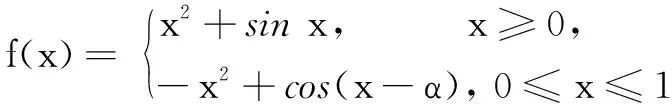
例题 已知函数
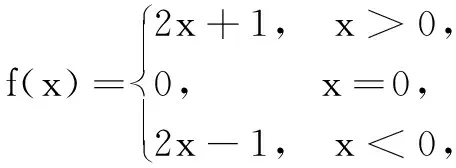
(2)参数问题
生3 已知函数
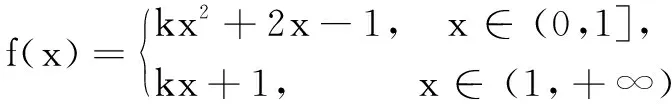
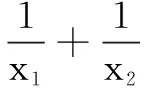
求解方法 一是参变分离;二是研究零点问题分类讨论.
生5 已知函数
在区间(0,+∞)上有且只有三个不同的零点,则实数m的取值范围是______.
说明 当函数里有lnx等时不易画图,应采用求导来判断单调性画出图象.
(3)图象
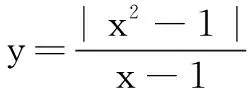
(4)求值
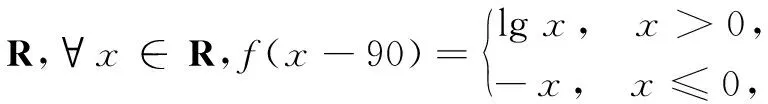
分段函数求值处理方法:分段研究,或借助图象解决.
费赖登塔尔曾说,“没有反思,学生的理解就不可能从一个水平升华到更高的水平”.因此,在紧张而忙碌的高三复习中,教师有意识地培养学生的反思意识,设置有效的反思训练活动,就可以提高学生独立思考问题、解决问题的能力,激活学生的智慧火花,提升学习数学的信心,进而提高高三数学复习的有效性.

