高中函数恒成立问题的解题策略
俞安琪
(江苏省扬州大学数学科学学院,225002)
函数恒成立问题是高中数学解题中较难的部分,它不但涉及到各类函数的图象和性质,而且和导数、数列等知识相联系,涉及的知识点比较多,所以也是历年高考中的一个热点.本文拟结合近几年各地高考及模拟题,给出解决高中函数恒成立问题的常见方法和解题策略.
一、利用函数性质
函数恒成立问题往往与函数的最值有关.例如,若f(x)>0恒成立,等价于f(x)min>0;若f(x)<0恒成立,等价于f(x)max<0.而函数的最大值和最小值的寻找,主要借助以下两种方法:一是直接利用函数的性质(即函数的奇偶性和单调性);二是根据题意构造新函数,并结合基本不等式解决问题.
解析 由题意可知,f(-x)=-f(x),所以f(x)为R上的奇函数,所以f(a-1)+f(2a2)≤0等价于f(2a2)≤f(1-a).

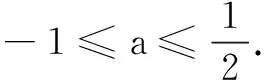
评析 在本题中,我们利用函数的奇偶性,将问题转化为f(2a2)≤f(1-a),再根据该函数的单调性,转化为不等式来解决.
例2 已知f(x)=ax-ex(a>0),当1≤a≤e+1时,求证:f(x)≤x.
解析 要证f(x)≤x.,即证x-f(x)≥0.构造函数g(a)=x-f(x)=-ax+x+ex,就只要证明g(a)≥0在1≤a≤e+1上恒成立.当a=1时,g(1)=-x+x+ex>0;当a=1+e时,g(1+e)=ex-ex,构造函数h(x)=ex-ex,则h′(x)=ex-e,当x<1时,h′(x)<0;当x>1时,h′(x)>0,所以h(x)在(-∞,1)上单调递减,在(1,+∞)上单调递增,所以h(x)≥h(1)=e-e=0,即g(1+e)≥0.
综上可知g(a)≥0在1≤a≤e+1上恒成立,当1≤a≤e+1时,f(x)≤x.
评析 该题利用构造函数的方法,将形如f(x)≤g(x)的问题,转化为f(x)-g(x)≤0恒成立的形式,构造成一个新函数,进而转化为研究新函数在指定区间上的最值问题.由于形式多样,所以在我们具体解答过程中要注意灵活多变.
在解题中,如果我们碰到一个函数的恒成立问题时,并且在题目中仅仅提供了函数的单调性、奇偶性,并没有提供函数的解析式,这个时候我们应该考查利用函数性质解决.
二、分离参数法
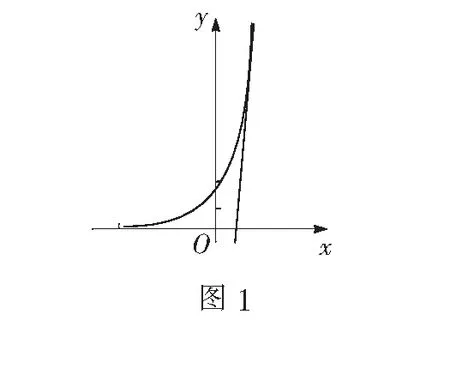
利用分离参数法来解决形如f(x,λ)>0的恒成立问题(其中λ为是参数),求参数λ的取值范围.我们通常采用以下几个步骤:第一步,将原函数中的参数和变量进行分离,即将原来的函数恒成立问题转化为g(λ)>f(x)或者g(λ) 但在使用这个方法时,我们也需要注意以下几点:一是参数是可以并且是比较容易与变量分离的;二是分离出来的函数的最大值或者最小值是可以比较容易算出来的. 评析 分离参数法是解决恒成立问题的一种重要方法,分离参数后,可以通过构造新的函数f(x).若参数a≤f(x),则a要小于等于f(x)的最小值;若a≥f(x),那么a要大于等于f(x)的最大值,并且在此类的求解过程中,大多都要应用基本不等式. 大多数函数恒成立问题都会使用到分离参数法.根据题意列出恒成立的式子并仔细观察,若将要求的参数放到不等式或者等式的一边,另一边的关系式可以根据题目条件判断其单调性,我们便可以采取该种方法. (1)基本思想 如果把等式或者是不等式,经过合理变形后,能够很容易地将等号或者不等号两边的函数图象画出来,则可以通过作图来直接判断结果.所以这种方法在我们做选择题或者填空题的时候就会显得尤其简便.在使用该方法的时候,我们需注意: 一是变形要合理.对于恒成立的式子,我们需要进行的是合理变形,而不是为了凑能够作出的图象而进行不正确的变形. 二是变形后的式子能较容易作出图象.变形后的式子一般都会符合基本函数的形式,也就是我们能直接绘制出函数图象,如果进行一阶求导后仍较为困难,则可以改变思路. (2)例题解析 例4 若函数f(x)=2ex-nx+15>0在实数集R上恒成立,则正整数n的最大值是______. 解析 题设等价于y=2ex的图象恒在y=nx-15的上方.分别作出这两个函数的图象(如图1),观察可知:当y=nx-15与y=2ex相切时,此时n是最大的. 设切点坐标为(x0,2ex0),因为y'=2ex,所以n=2ex0,切线方程为 y-2ex0=2ex0(x-x0). 又因为y=nx-15恒过点(0,-15), 将此点代入切线方程可得:2ex0(x0-1)-15=0,设g(x0)=2ex0(x0-1)-15在(1,+∞)上递增又因为g(2)<0,g(3)>0,所以x0∈(2,3),所以n=2ex0∈(2e2,2e3),又因为y=2ex的图象恒在y=nx-15的上方所以n≤2ex0≤2e2,而2e2∈(14,15),所以n的最大值为14. 评析 该题我们若把函数f(x)=2ex-nx+15看作是一个整体去讨论单调性,求导之后可得f′(x)=2ex-n,很难完成我们所要求的问题.当我们换种思路,发现函数f(x)是我们熟悉的两种基本函数组成的,即指数函数h1(x)=2ex和一次函数h2(x)=-nx+15组成的,而讨论这两个函数对大家还是很容易的,观察图象后,发现求n的最大值可以转化为相切问题,从而顺利解决该题. 数形结合是高中数学解题中的一种相当重要的解题方法.在利用该方法时,关键是可以分离出能够讨论的形,即你知道的能够作出的形,这就要求同学们认真分析题干,认真审题.在解决恒成立问题时,尤其是选择题或者填空题,若发现给出的函数是由基本函数组成的,这个时候可以尝试采取数形结合法. 对于一些含参的恒成立问题,在分离参数的过程中,往往会产生各种问题,或者在分离出参数后,求有关函数的最大值或者最小值比较困难,此时,我们不妨考虑把主元和参数换个位置,可能比较容易解决原本困难的问题. 解析f′(x)=ax2-3x+(a+1),由题设可知a(x2+2)-x2-2x>0对∀a∈(0,+∞)恒成立.设g(a)=(x2+2)a-x2-2x,则g(a)是一个以a为自变量的一次函数.因为x2+2>0,所以g(a)在(0,+∞)上单调增,所以对∀a∈(0,+∞),g(a)>0成立,即g(0)≥0,即-x2-2x≥0,所以-2≤x≤0. 评析 本题中,若将x看作是主元,我们将得到一个二次函数,在分离参数之后,是一个分式的形式,我们需要变形求导之后才能得到想要的结果.在这个过程中,可能要涉及到分类讨论,加大了学生得到正确答案的难度.但如果我们将a看作是主元,那么我们将会得到一个以a为自变量的一次函数.我们都知道一次函数的讨论在很大程度上比二次函数简单,在接下来的问题处理上也相对容易.所以在分离参数求最值遇到麻烦时,可以考虑主元和参数互换位置,再综合运用其他知识,说不定有更好的效果.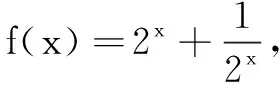
三、数形结合法
四、主参换位法


