多维切入 “核心”绽放

桑树林

(江苏省睢宁高级中学北校，221200)

《普通高中数学课程标准》定义数学核心素养为:具有数学基本特征思维品质、关键能力以及情感、态度与价值观的综合体现，数学核心素养与数学教育的终极目标有关，表达了“学生应具备的、能够适应终身发展和社会发展需要的必备品格和关键能力”.那么，如何让核心素养在一线课堂落地生花、完美绽放呢?下面笔者通过一节“隐形圆”的公开课来呈现其核心绽放的过程,凸显多维切入的作用.

一、情境导入再现

研究背景 此前笔者计划开设一节关于隐形圆的公开课，便有意先将下面这样一个问题抛给学生，让学生自行研究.

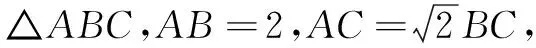
本题属于三角形边角关系问题,主要考查数形结合、转化化归等思想,同时对学生的逻辑推理能力、想象能力和运算能力都提出了更高的要求,属于中档题.结果发现学生能在规定时间计算出准确结果的很少,切入点的选择具有高度的相似性,值得深思.

通过批改学案,笔者发现很多同学都将目光汇聚于边的比例,设CB=x并利用三角形的面积公式来获得函数关系.(前台展示)

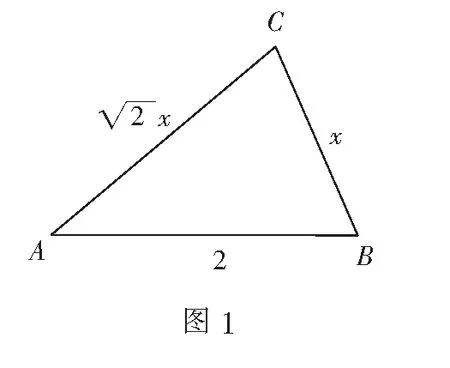
切入点1 用数学的思维去思考(多数学生观点)

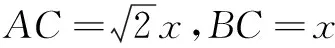
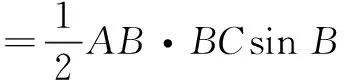
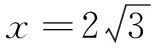
通过余弦定理和面积公式很容易构建函数关系,方法常规，便于操作,这是多数学生选择切入点1的根本原因.切入点1对学生的逻辑推理能力和数学运算能力要求较高,这恰恰体现了数学思维的严谨性，但也暴露出很多学生对范围把握不准和计算存在短板等问题,对题目的内涵和外延挖掘得还不够,我们理应再进一步去探索和拓展.

切入点2 用数学的语言去表达

课上教师引导学生观察AC和BC的比例关系,提醒学生也可从“数量”入手,用更加代数化的语言来呈现质同形异的解题方案.此时便有个别学生想到了两点间距离公式,从而解决问题.

以AB所在直线为x轴,以AB中点为坐标原点,建立如图2所示的直角坐标系.则A(-1,0),B(1,0).

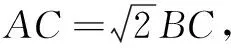
整理得y2=-(x-3)2+8.

(*)

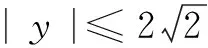
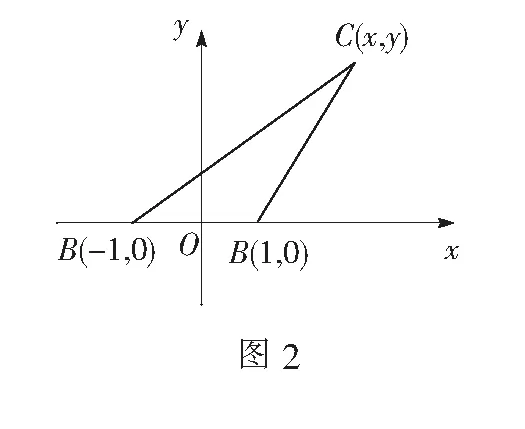
学会用数学语言是指学会数学建模、善用数据分析等解决问题,保证数学应用的广泛性.切入点2提示学生通过建立平面直角坐标系,从另外一个维度去探寻数量之间的关系,实现几何关系的代数化,建立更加理想化的函数模型求解问题.当然,我们的追求远不止于此,从数形结合的角度看，也许还有惊人的发现,鼓励学生进行小组交流与探究,看看是否能获得最优解.

学生似乎没有更为积极的互动,经过长时间的讨论也难以发现“圆”的影子,很是着急.此时笔者想起华罗庚先生的一句话“形缺数时难入微,数缺形时难直观”,于是启发学生，我们面对上述表达式难道没有发现更为熟悉的几何关系吗?通过移项再观察,学生豁然开朗,此时课堂气氛也达到了顶峰.

切入点3 用数学的眼光去观察

上述解法中的(*)式移项变形为(x-3)2+y2=8(y≠0).

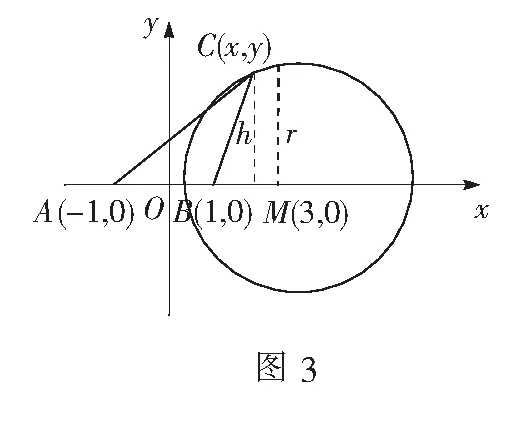
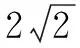
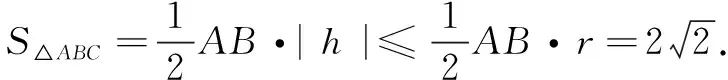
数学的眼光是指学生能通过数学抽象(符号意识、数感)、直观想象(几何直观、空间想象能力)的能力素养去分析问题,保证数学的一般性.切入点3通过表达式的转换,去发现“阿波罗尼斯圆”的影子,进而回归几何关系解决此题,不禁让人眼前一亮,似乎整个题目的讲解都得到升华，学生学科素养得到完美绽放,令人激动万分.

二、课堂实录观察

1.再现问题多维切入流程图(图4)

2.注重多维切入,构建生态课堂

所谓“多维切入”，即是引导学生从多个视角寻找解决问题的突破口,充分调动学生学习的积极性和创造性,激发学生潜能,养成多维立体思考习惯.让更多的学生参与进来,构建更加和谐和极具活力的生态课堂,真正地让学生成为课堂的主人,体现以学生为主体的育人理念.

在教学中,经常会有学生反映说“能听懂老师所讲,但自己一做就不会”；也有学生反映说“能看懂课本上的内容,但自己独立做题就不会”；还有学生说“曾做过的题,过了一段时间或换一下条件就又不会做了(或又做错了)”.教师课下交流的时候,通常也抱怨“同类型题,以前练习过,讲评过,为什么错误率还这么高?”相识的场景不断重现,学生迷茫，教师无奈,造成了一种奇特的高原现象，“学而有困，潜而不能”，即学生有学习的意识却经常遇到无法逾越的困难,学生有学习的潜能却不具备解决问题的水平.

笔者认为，出现上述现象的根本原因是学生在学习的过程中更多的是被动接受,很少有主动发挥和想象,个人潜能无法释放.教师充满激情的讲解在学生面前尽显苍白和无力,不能形成良好的生生互动、师生互动的生态效应.如果教师在教学中讲解有余,多维切入的训练不足,久而久之，学生便会失去学习的兴趣和动力,师生之间的就不会出现良性互动.倘若教师在讲解过程中注重引导学生多维度切入,势必会调动绝大多数学生学习兴趣,让更多的学生参与到课堂中来,释放潜能,真正打造具有活性的生态课堂

三、多维切入，力促“核心”绽放

1.高中数学核心素养透视

高中数学课程标准把数学核心素养定义为“学生应具备的、能够适应终身发展和社会发展需要的、与数学有关的关键能力和思维品质”,由此提出了把抽象思维、逻辑推理、直观想象、数学建模、数学运算、数据分析作为高中数学的六大核心素养,体现了数学学科的本质与功能目标,也就是育人价值.那么，其功能目标是什么?这里用史宁中教授的话来诠释是最恰当不过的,“就是让学生会用数学的眼光观察现实世界,会用数学的思维思考现实世界,会用数学的语言表达现实世界”.

数学核心素养对数学学科的教学有指导和引领的作用,彰显了学科教学的育人价值.因此，这就要求数学学科教学的目标和活动都要从素养的高度来进行,为素养而教,用学科育人.但是数学核心素养的达成也必须依赖于数学学科本身独特育人功能的发挥,以及对学科本质魅力的发掘.所以说,数学核心素养反映的是数学本质、数学思想与数学思维方法,它是在学生参与相关的数学学习活动过程中逐渐形成的,可以在遇到问题的时候,即使不是数学问题也可以从数学的角度和用数学的思维方法去思考、分析、理解和解决问题,具有综合性、整体性和持久性.

2.如何实现“核心绽放”

“核心绽放”就是让高中数学的六大核心素养能够在一线课堂有多维立体的显现.教师应该深入地研究核心素养的内涵与外延,并合理地运用到教学中去.让学生从不同的维度理解问题,实现问题解决方案的多样化和师生之间的良性互动.

多维切入的培养也许没有固定的模板可以借鉴,核心绽放的界定也许未必统一.但是解题流程图说明,多维切入可以为学生提供更为广阔的视角去尝试理解问题,提供更多的切入点去破解迷局,提供更多的方法去合理地解决问题,提供更多的数学思想去感悟和升华,更为难得的是激发了大多数学生的学习兴趣.正所谓尺有所短寸有所长,每个学生的潜力都是相对均衡的,但是在学习和生活中,对于某一件事物的认知理解能力又存在着一定差别.每个学生解决问题的着力点不一样,通过多维切入鼓励学生通过逻辑推理、数学建模、数学抽象、直观想象、数据分析和数学计算等方式处理问题,突破“学而有困潜而不能”的高原现象,让核心素养落地生花，完美绽放.