浅议“阿波罗尼斯圆”的应用

章建锋

(江苏省梅村高级中学，214112)

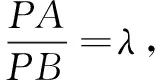
在近几年江苏高考和各地模拟考试中,频频出现有关“阿波罗尼斯圆”的问题．本文主要介绍“阿波罗尼斯圆”在优化解题,培养学生解题习惯,增强学生数学信心方面的作用.希望能带给大家一定的帮助．

一、“阿波罗尼斯圆”的正用

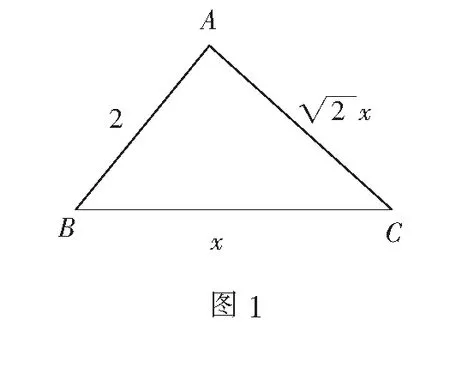
高考考试说明上给出的说明是:“命题者本意考查三角形面积公式、余弦定理及函数思想．”可谓立意新颖,题意简明,但是运算处理有一定难度．求解如下:

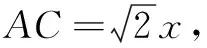
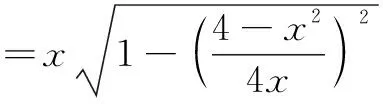
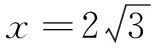
可此题若从轨迹的角度去求解,即在平时的教学中,注意渗透了“阿波罗尼斯圆”的定义,则该题的解决不但简洁明了且运算简捷．求解过程如下:

因为AB=2(定长),所以可以AB所在直线为x轴,以它的中垂线为y轴，建立如图2所示的平面直角坐标系,则A(-1,0),B(1,0).

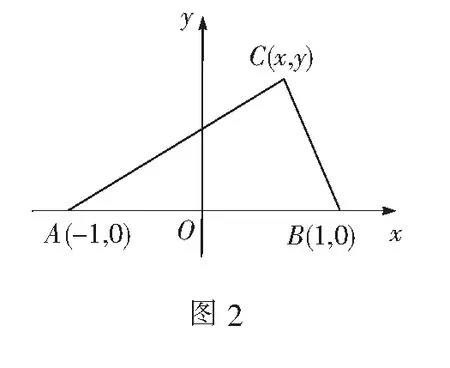
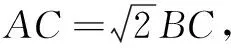
化简得(x-3)2+y2=8 (y≠0).

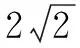
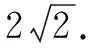
详析 如上解法简洁,省去求解变量取值范围的过程,又避免了复杂的运算．

其实,象这样来源于数学史的题型不胜枚举,在平时的教学中，如果我们能够较多地渗透,对于进一步培养学生的数学学习兴趣,有极大的帮助．

二、“阿波罗尼斯圆”的逆用

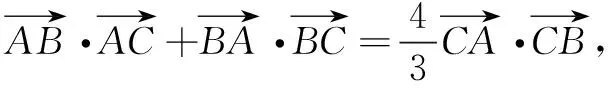
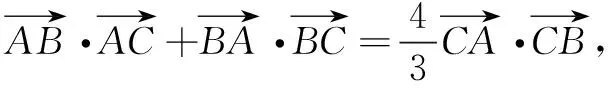
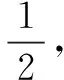
(1)设存在定点E(a,b),使得满足CE=λCB(λ>0且λ≠1)的点C的轨迹方程为

(x-1)2+y2=4,即x2+y2-2x-3=0.

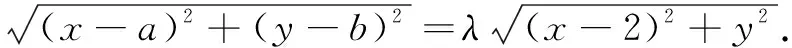
化简得点C的轨迹方程为:

又点C的轨迹方程为x2+y2-2x-3=0,所以得到

∴存在定点E(5,0),使得满足CE=2CB的点C的轨迹就是M．

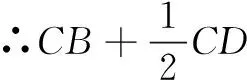
(2)设存在定点F(m,n),使得满足CF=μCD的点C的轨迹方程为x2+y2-2x-3=0.

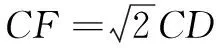
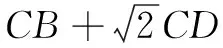
大家都知道，对已有知识进行新定义,已经成为高考的一大亮点,这就要求教师学生面对陌生的题目背景,能迅速提取有用信息,善于挖掘概念的内涵与本质,并合理迁移,运用已学的知识加以解决．