直观引领 归纳提升*——以“多面体的外接球问题”教学为例

王建鹏

(福建省惠安高级中学，362100)

党的十九大明确提出立德树人的根本任务,学科核心素养作为育人价值的集中体现,是需要学生在学科学习和应用的过程中逐步形成和发展的．数学学科核心素养包括:数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析．其中,直观想象是指借助几何直观和空间想象感知事物的形态与变化,利用空间形式特别是图形,理解和解决数学问题的素养．其主要表现为:建立形与数的联系,利用几何图形描述问题,借助几何直观理解问题,运用空间想象认识事物．

多面体的外接球问题是立体几何教学中的一个重点,也是近几年高考的热点,研究多面体外接球的问题,既要熟练运用多面体的有关几何元素与球的半径之间的关系,更需要在直观想象核心素养的引领下,动态观察形成数学直观,在具体的情境中感悟外接球问题的本质．以下是笔者在执教一堂面向高一学生的“多面体的外接球”公开课后,从直观想象的核心素养视角出发,对教学过程的一些实践与反思．

基于课程标准和学生情况的实际,确定本节课的教学目标为:经历“寻找外接球球心”的过程,理解“补形”的思维成因及意义,会根据多面体的几何特征选择解决外接球问题的相应方法,厘清直三棱柱与三棱锥外接球球心位置的一般规律．以下是教学流程分析.

一、提出问题,引入新课

引例 已知长方体ABCD-A1B1C1D1的各顶点都在球O的球面上,若AB=AD=1,AA1=2,则球O的半径为______.

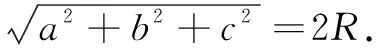
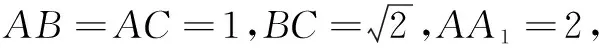
本题中图形的几何特征:底面为直角三角形的直三棱柱；对应的解决方法:补形为长方体,直接运用结论．

变式1 已知直三棱柱ABC-A1B1C1的各顶点都在球O的球面上,若AB=AC=BC=1,AA1=2,则球O的半径为______.

本题中图形的几何特征:底面为等边三角形的直三棱柱；对应的解决方法:找球心,球心位于两底面正三角形中心连线的中点位置,并结合勾股定理．

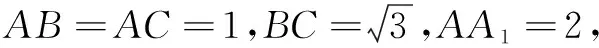
变式中图形的几何特征:一般的直三棱柱.

对应的解决方法:找球心,球心位于两底面三角形外心连线的中点位置,或通过正弦定理求出底面三角形的外接圆半径,并结合勾股定理．此方法同样适用于圆柱的外接球问题．

问题1 通过例1及其变式,你能归纳出求直三棱柱的外接球半径的方法吗?关于直三棱柱的外接球球心位置,你有什么结论?

引导学生总结归纳方法:一是补形为长方体(涉及两两垂直条件)；二是找球心(球心到各顶点的距离相等即为半径).

得出结论:直三棱柱的外接球球心位于两底面三角形外心连线的中点位置.

二、直观引领,类比联想

问题2 类比求直三棱柱的外接球半径的方法,如何处理三棱锥的外接球问题?

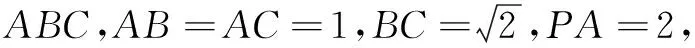
本题中图形的几何特征:侧棱垂直于底面且底面为直角三角形的三棱锥.

对应的解决方法:补形为长方体(墙角型),直接运用结论．

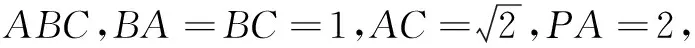
变式中图形的几何特征:侧棱垂直于底面且底面为直角三角形的三棱锥.

对应的解决方法:补形为长方体(三节棍型),直接运用结论．

变式2 已知三棱锥P-ABC的各顶点都在球O的球面上.若PA⊥平面ABC,AB=AC=BC=1,PA=2,则球O的半径为______.

变式中图形的几何特征:侧棱垂直于底面且底面为等边三角形的三棱锥.

对应的解决方法:补形为正三棱柱．

变式3 已知四棱锥P-ABCD的各顶点都在球O的球面上.若平面PAB⊥平面ABCD,∆PAB是边长为1的等边三角形,四边形ABCD是边长为1的正方形,则球O的半径为______.

变式中图形的几何特征:类似于变式2的图形.

对应的解决方法:补形为正三棱柱.

师生活动:投屏结合板书讲解.

例3 已知正三棱锥P-ABC的各顶点都在球O的球面上,若侧棱长为2,底面∆ABC是边长为1的等边三角形,则球O的半径为______.

本题中的图形的几何特征:正三棱锥.

对应的解决方法:找球心,球心位于顶点P与底面正三角形中心的连线上,即位于过顶点P的三棱锥的高上,并结合勾股定理求解．

变式 已知正四面体P-ABC的各顶点都在球O的球面上.若各棱长均为1,则球O的半径为( )

变式中图形的几何特征:正四面体.

对应的解决方法:一是找球心(球心位于顶点P与底面正三角形中心的连线段的靠近底面的四等分点);② 补形为正方体(所有的棱为正方体的面对角线).

师生活动:利用智慧教室,对每个错误选项进行错因分析．

同步拓展:三组对棱分别相等的三棱锥的外接球问题,可将此三棱锥补形成长方体．

三、探究思考,归纳提升

问题3 类比关于直三棱柱的外接球球心位置的结论,对于一般性的三棱锥外接球球心位置,你有什么见解?

师生活动:通过学习微课,总结出找三棱锥的外接球球心位置的通法．

解决方法:沿着其中两个面的三角形外心作垂线,两垂线的交点即为外接球球心．

课后提升

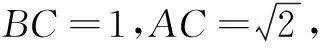
几何特征:可补形为例2的变式3图形.

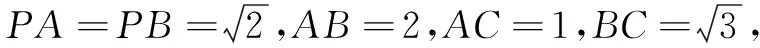
几何特征:球心即为线段AB的中点

本节课以直三棱柱与三棱锥为代表,探求多面体外接球问题的解决思路,并对直三棱柱与三棱锥的外接球球心位置进行了归纳梳理．结合本节课的教学目标,笔者认为重点应思考直观想象在教学中的孕育点与生长点,注意其与教学内容的关联,从而积极引导学生用数学眼光观察世界,用数学思维思考世界,用数学语言表达世界,把数学学科核心素养的提升落到实处．