注重培养高中学生的数学建模意识

刘达锋

(广东省阳江市第一中学，529500)

《普通高中数学课程标准》拟定了6个数学核心素养,分别是抽象能力、逻辑推理与交流、建模能力与反思、运算能力、几何直观和空间想象、数据分析与知识获取．其中，数学模型构建了数学与外部世界的桥梁,是数学应用的重要形式．是应用数学解决实际问题的基本手段,也是推动数学发展的动力．研究表明，“知道数学建模是什么的意思”的同学为25.4%,“听说过但不知是什么”的同学为62.02%，“没听说过”的同学为12.94%．针对这一现状,在教学中培养高中生的数学建模意识就显得尤其重要．

谈起数学建模,高中老师都觉得很不自信,这好像应该是大学老师做的事情,高中老师似乎还没有培养学生数学建模能力的“功力”.笔者倒觉得数学建模其实离我们并不遥远．例如在“离散型随机变量的均值”教学中有这样一个问题:

问题 某商场要将单价分别为18元/kg,24元/kg,36元/kg的3种糖果按3∶2∶1的比例混合销售,如何对混合糖果定价才合理?

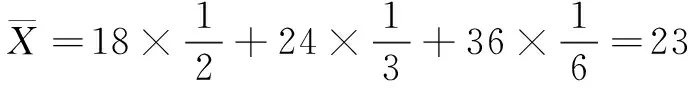
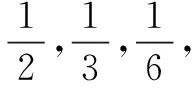
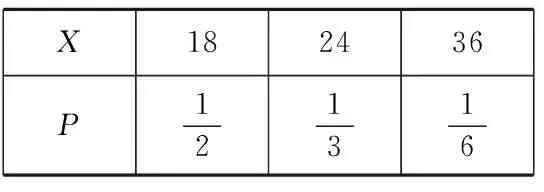
X182436 P121316

因此，权数恰好是随机变量X的分布列,这样每千克混合糖果的合理的价格可以表示为18×P(X=18)+24×P(X=24)+36×P(X=36).

一般地,若离散型随机变量X的分布列为

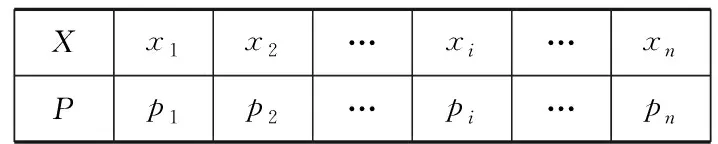
Xx1x2…xi…xn Pp1p2…pi…pn

则称EX=x1p1+x2p2+…+xipi+…+xnpx为随机变量X的均值或数学期望，它反映离散型随机变量取值的平均水平．

通过一个糖果混合模型的学习,从具体到抽象,从特殊到一般,让学生能直观形象地感受和理解离散型随机变量的均值,而不再是生硬地记住一个结论．这就是数学建模带给高中数学的魅力．

培养高中学生数学建模能力,首先要培养学生数学建模意识．但培养学生数学建模意识不是一朝一夕的事情,需要把数学建模意识贯穿在教学的始终,使数学建模意识成为学生思考问题的方法和习惯．现在就如何在课堂教学中培养学生的数学建模意识做一些初步的探讨．

一、概念教学中渗透数学建模意识

建构主义认为，学习是一个意义建构的过程,是学习者通过新、旧知识经验的相互作用,来形成、丰富和调整自己的认知结构的过程．概念是客观事物的本质属性在人们头脑中的反映,数学概念的教学既是数学教学的重要环节,又是数学学习的核心,是学生思考问题、推理证明的依据．数学概念的学习是学习数学知识的第一步,在概念的教学中渗透数学建模意识,能为高中学生数学建模意识的培养和数学建模能力的提升打下坚实的基础．

案例1 圆的标准方程的概念教学

1.创设情境,引入课题

问题1 展示生活中与圆有关的图片并请学生找出这些图片中物体的相同之处,举出生活中与圆有关的例子．

(答:汽车轮胎,方向盘,升起的太阳,摩天轮,隧道等)

问题2 什么是圆?初中时我们是怎样给圆下定义的?请同学用尺规作出一个圆的图形．

2.深入探究，获得新知

在平面直角坐标系中如何确定一个圆的方程呢?

建立平面直角坐标系xOy，设圆心的坐标为A(a,b),半径为r.

点M(x,y)为圆上的任意一点(如图1),则|MC|=r.

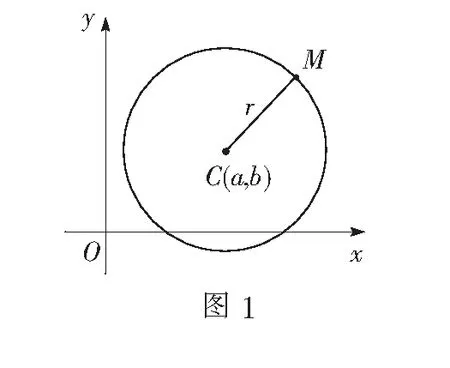
圆心为A的圆就是集合

P={M||MA|=r}.

由两点间的距离公式,得

将上式两边平方,得

(x-a)2+(y-b)2=r2，

所以圆的标准方程为

(x-a)2+(y-b)2=r2.

特别地,当圆心为坐标原点O(0,0)时,半径为r的圆的标准方程为x2+y2=r2.

评注 结合实际模型对圆的标准方程的概念教学,通过动手作图，使学生能直观感受和理解圆的图形结构,激发学生学习的积极性．教师引导,循序渐进,层层深入,给学生提供一个自主探索学习的机会．让学生经历“建坐标系—设坐标—列式—代入—化简”推导圆的标准方程的过程，不仅能使学生认识到圆的图形的特点,还能掌握圆的标准方程的推导过程,更能深刻理解圆的标准方程．这种依据实际问题,提出问题,解决问题的思想不正是数学建模思想吗?当学生有这样的一种数学建模意识,那么，在椭圆、双曲线、抛物线的教学中就会如鱼得水．

二、例题讲解中融入数学建模意识

例题作为学以致用的重要环节,在教学过程中担负着把知识转化为能力的重要使命．从结构上看,例题是把知识、技能、思想和方法联系起来的一条纽带．知识的价值、技能的操作、思想与方法的作用都是通过例题来体现的．例题讲解对学生的思维及解题行为起着潜移默化的作用,是启迪学生掌握解决各类数学问题的钥匙．可见在例题讲解中创设情境,融入数学建模意识,对于培养学生的数学建模意识和提高学生的数学建模能力起着非常重要的作用．

案例2 几何概型例题的教学

例题 甲、乙在6时到7时之间在某处会面,并约定先到者应等候另一个人一刻钟,过时即可离去,求两人能会面的概率.

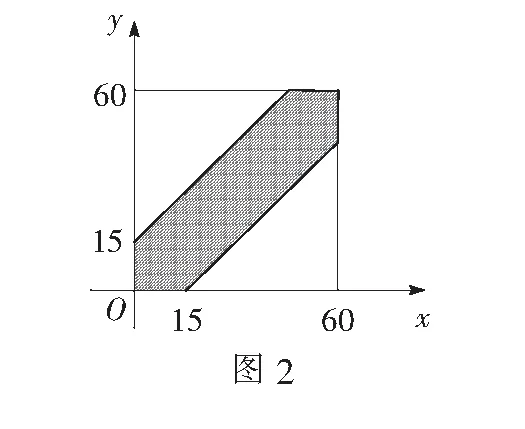
解 设甲、乙两人到达的时间分别用x、y表示,记为(x,y).因甲、乙两人都是6时到7时之间,即60分钟内,故试验的全部结果构成的区域Ω={(x,y)|0≤x≤60,0≤y≤60},如图2.

SΩ=60×60=3 600.

设甲、乙两人能会面的事件为A,则

A={(x,y)||x-y|≤15,0≤x≤60,0≤y≤60}.

SA=3 600-45×45=1 575，

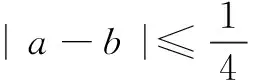
三、作业设计中体现数学建模意识

作业设计结合实际教学案例,对基本知识和基本技能具有巩固和强化的作用．著名的德国心理学家艾宾浩斯提出了遗忘曲线,他认为遗忘在学习之后立即开始,而且遗忘的进程并不是均匀的．最初遗忘速度很快,以后逐渐缓慢,到了相当长的时间后,几乎就不再遗忘了,即呈现“先快后慢”的特点．在作业设计中体现数学建模意识就显得十分必要．有利于巩固和强化学生的数学建模意识和提高学生数学建模能力．在作业设计中体现数学建模意识并不是很难的事情．根据作业设计的巩固性原则、针对性原则,加入相应的应用背景材料,一道体现数学建模思想的作业题应然而生．

案例3 正余弦定理的作业设计

作业 如图3,为测量山高MN,选择A和另一座山的山顶C为测量观测点.从点A测得点M的仰角∠MAN=60°,点C的仰角∠CAB=45°以及∠MAC=75°;从点C测得∠MCA=60°，已知山高BC=100 m,则山高MN=______m.

评注 通过设计一个测量山高的问题,让学生透过问题,看到本质,用数学的眼光来看待问题,应用数学方法来解决问题，进而巩固和强化学生的数学建模意识．

总之,提高学生数学建模能力,首先要培养学生的数学建模意识．在教学中培养学生的数学建模意识，不仅对高中数学教学有重要的作用,还对提高学生应用数学解决问题的能力以及学生的长远发展都有深远意义．