数学函数教学策略探析

高春发

(福建省南平市光泽县止马中学 354101)

函数相关知识常常是学生产生混乱的知识模块，由于函数知识模块较为抽象，需要学生能够以严谨的逻辑思维进行分析，所以在教学过程中教师应采用多种教学方式，以多样化的教学模式进行深入教学，能够更好地提高学生对于函数知识的认识与掌握.本文从函数模块入手，探讨如何在函数知识教学中以多种方式提高教学效果，更好地激发学生学习兴趣，掌握函数知识要点.

一、运用对比方法

对比教学法是常用的教学方法，其将不同的知识进行相似之处的对比，能够更好地区分知识间的不同，也能够在对比教学的过程中完善学生所学知识的框架，更好地帮助学生厘清知识体系.例如一次函数与反函数的对比，在教学过程中，教师可以通过“y=kx+b”与“y=k/x”，对其中的“k”的含义进行对比.在对比教学中，可以结合一次函数与反比例函数图象进行对比.“同学们，根据这两幅图象，大家可以自由代入数字，描绘出函数图象，并探讨一下k在一次函数与反比例函数中起到的作用，并探讨一下k与b的取值范围.”在经过代入、描点分析后，学生能够清晰地回答出“在一次函数中，k>0时，y随着x增大而增大；反比例函数中，k>0时，分别在第一象限内，在第三象限内，y随着x增大而减小.”这是相同字母在不同函数中对比所能够产生的知识要点的认知.同理，教师还可以通过其他的字母或转换字母位置进行对比的方式，帮助学生厘清对于固有知识形态的思路.例如教师可以出题.“画出y=ax+b，与y=b/x的所有可能性图象.”在这个例题中，将一次函数中的k值与反函数中的k值转化为了a与b，并且反比例函数中的系数b还与一次函数中的b值相关.在这种学生自主的构图中，教师可以明确地发现学生对于所学知识的掌握程度，并通过一次函数与反函数k、a、b之间关系的比较形成较为清晰的教学逻辑，更好地引导学生摆脱固有观念，在函数学习中形成清晰的认知.

二、“数形结合”方法

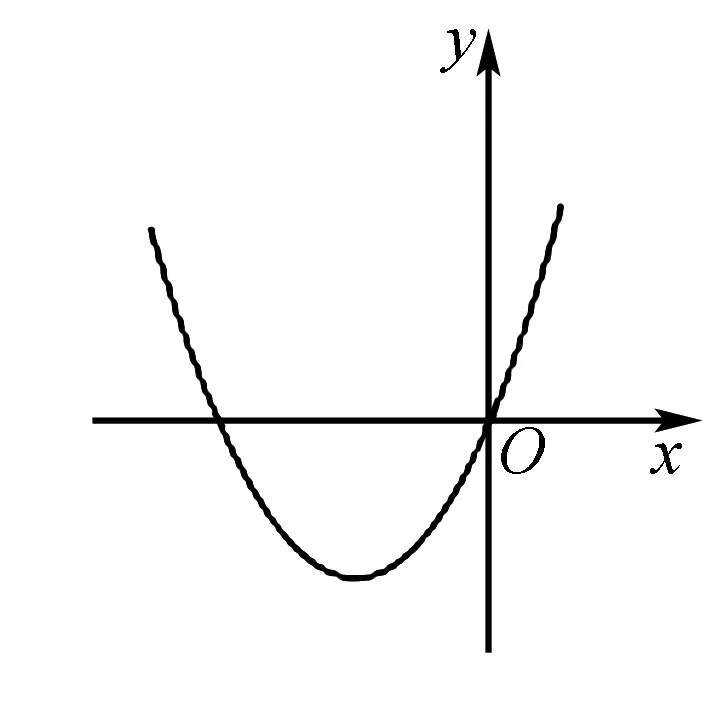
图1

图2

函数教学中，数与形的结合是将抽象的数学知识转化为具象数学图形的良好方式.在数学教学过程中，教师应重视数与形的结合教学.以二次函数的教学为例，在教学过程中，将二次函数“y=ax2+bx+c”中a、b、c的含义在图象中表现能够更加直接地向学生传授一次项系数、二次项系数与常数项的根本意思.例如以“x2+3x>0时x的取值范围”进行分析，在常规做法中，学生会先通过数学计算方法在“x2+3x=0”中进行计算，算出在y等于0情况下x的取值情况，也就是算出二次函数图象与x轴的交点，但如何快速地判断取值范围，还需要有结合图象的意识.通过二次项系数1大于0可以知道二次函数图象开口向上，当y=x2+3x大于0时，x的取值范围应在两个交点0、-3的左右两边，如图1.

以数形结合的方式进行教学，学生能够在函数知识中快速进行图形的判断，更好地对题目中的问题进行解答，不仅有利于学生数学意识的强化，还能够较好地在解题过程中结合图形简化题目要求.例如在“y=-2(x-2)2+8”中，以顶点式的方法能够快速判断二次函数的对称轴、顶点、开口方向，能够在较短的时间中画出函数图象，如图2，有利于进行后续的解题.

这种数形结合思想是教师在教学中应引导学生主动形成的学习习惯，能够更好地提高学生对于函数知识的正确认识，减轻学习压力.

三、实例演练教学方法

传统的讲授式教学在当前的教学领域中已经难以发挥有效作用，多种教学方式的应用是提高学生对于数学知识认识的方式.当前在教育教学领域中，多媒体工具的使用已经较为频繁，教师在教学过程中也能够很好地应用多媒体工具进行实例演练教学，不仅有利于提高学生学习专注力，还能够较好地激发学生学习兴趣，掌握函数知识.例如“已知抛物线经过点(5，-3)，其对称轴为直线x=4，则抛物线一定经过的另一点的坐标是什么？”教师在教学过程中可以进行对称轴知识的引入.“在抛物线上存在两个相互对称的点，对称轴为抛物线的对称轴，那么两个对称点的什么值不会改变？”通过教师以多媒体方式构建图形引导学生，学生能够发现对称点间y值不变，x值随对称轴变化而变化.学生能够回答“另一点坐标为(3，-3)”.通过教师的实例教学，可以提供给学生相似的例题，起到加强知识要点记忆与巩固知识点的作用.如“已知抛物线经过点(0，-2)，其对称轴为直线x=-6，则抛物线一定经过另一点的坐标是什么？”这种实例演练式的教学方法能够让学生在接受某种知识后即时性地巩固知识，有利于加深学生对于知识要点的认识，更好地应用于其他综合性的练习中，提高函数知识的学习效果.

函数知识的学习有一定难度，其本身具有一定抽象属性，需要学生在学习过程中能够以严谨的逻辑思维进行知识点的理解与掌握.在教学过程中，教师可以使用多种教学方法如对比教学法、数形结合法、实例演练法等，通过多种教学方法的共同应用，能够较好地解决函数教学中的抽象化问题，更好地提高学生对于函数知识的掌握程度，提升数学函数的教学效果.