问题设置提升思维层级策略研究——以初中数学课堂教学为例

缪 炯

(浙江省杭州市勇进实验学校 310000)

在数学课堂中，教师为了启迪学生的思维，发展学生的探究能力，通常是采用提问的方式，引导学生思考.教师在进行问题设置时，首先应该满足以下基本要求：语言组织严谨；问题要有序且有度；问题设置的目的明确；问题既要有全体性，又要不失差异性等等.问题是数学思维的核心，是数学的灵魂.真正好的问题，并不仅仅是让学生通过思考得出答案，而是让学生在解答的过程中，帮助学生掌握科学的思维方法，养成良好的思维习惯.

一、创设学生感兴趣的问题情景进行设置，激发学生学习兴趣

为了有效地实现教学目标，教师应该运用多种教学方式，为学生设置形式丰富的教学环境.首先根据教学内容创设学生感兴趣的问题，激发学生主动参与的积极性.例如九年级上册第三章圆的第三课时《垂径定理》教学设计片段：

问题1：给每位同学一张圆形的纸片，请问：你能找出纸片的圆心吗？

问题2：那么现在，老师把纸片换成硬币，你能找出它的圆心吗？

问题3：那么，你们能继续用这个方法，找出公园里圆形大草坪的圆心吗？

初中数学具有抽象性，绝大部分内容都是理论知识，因此不可避免的会比较枯燥.因此，教师要积极采取措施，根据学情结合生活实际，充分挖掘教材内容，设置能够激发学生探究意识的问题，培养学生创造性思维.

二、设置悬疑性问题，培养学生的问题意识

在设置问题的时候，教师可以引导学生根据问题产生质疑，进而提出新的问题，培养学生的问题意识.教师的问题可以是学生原有认知基础上的一种反问，帮助学生提出批判性问题，从而寻求出解决问题的正确途径.例如浙教版九年下册第二章第一课时《直线与圆的位置关系》的教学片断设计：

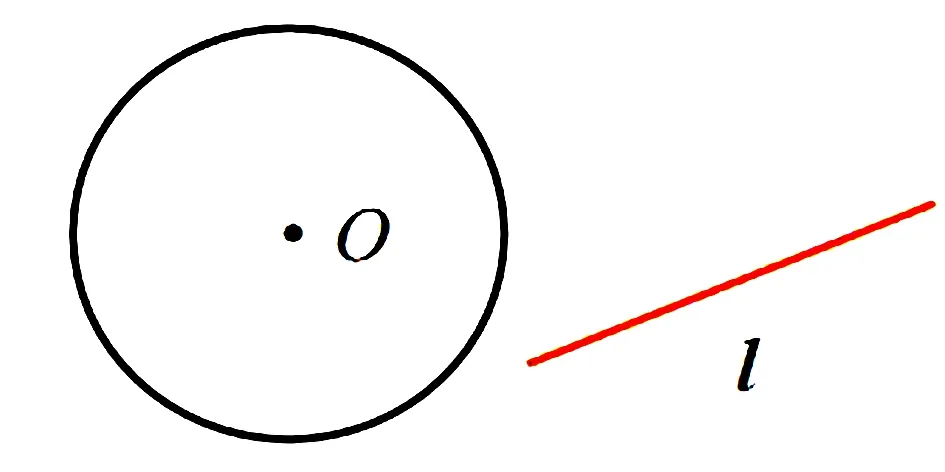
问题1：请判断如图所示的直线与圆的位置关系.

生：不知道直线和圆有几个交点，无法判断.

问题2：能否像判断点与圆的位置关系一样进行量化分析呢？

问题3：那么如何来衡量直线与圆位置的远近呢？要抓住哪两个关键量？

问题4：请按这个思路分析当d=r时，此时直线与圆有几个公共点？为什么？

问题5：为什么当d>r时，直线与圆没有公共点？当d

设计意图：在教学过程中，教师应当结合学生的认知水平，利用他们的思维盲区设置悬疑性的问题，极大地激发学生的求知欲，引导学生积极主动地参与到数学的学习当中.

三、设置问题要有梯度，有效拓展学生的思维

针对不同层次的学生，既要有基础性的问答题，又要有理解型的问题，最后再用难度较大的拓展题提升学生思维层级.当然这也要求教师要把握问题的难度，把一些学生比较难以理解的问题分解为环环相扣、步步分解的小问题，让学生易于理解和接受.

例如九上第三章《圆》的第二课时的教学：

第一步，问：经过一个已知点能作多少个圆？当学生回答无数个之后，教师不要急于马上提问两个点时的情况，应该再追加一问：为什么此时可以作无数个圆？让学生领悟到，只要改变圆心或者是半径这两个中任意的一个因素，圆就会改变.

第二步，在探索过两个已知点能作多少圆时，笔者曾尝试直接抛出问题：过A、B两点的圆的圆心在怎样的一条直线上？但是课后反思发现学生无法真正理解此问的目的，而是从迎合老师的角度猜测出问题的答案.基本都是先猜出答案再进行验证，并不是从确定圆的基本条件的两个要素出发，根据这两个要素的性质找到圆心在中垂线上.

因此笔者把此问继续分拆，首先提问：能找到一个过AB两点的圆吗？学生回答AB中点后，再继续提问，那你还能找出第二个吗？追问：那么，圆心需要满足哪些条件？引导学生最终找出确定圆的基本条件是：确定圆心和圆的半径.学生在明白此问的目的之后，便会继续思考，继而找出第三个第四个，然后总结得出过AB的圆心在AB的中垂线上.

第三步，教师继续提问：现在我们要过不共线的三点作圆，首先仍然需要先考虑确定圆的基本条件是什么？

教师设置的问题要能吸引学生主动的投入到课堂中，帮助他们深刻地体会确定圆的基本思想，反复强调，反复应用，树立了他们对新知识的正确认知.这样的问题设置，符合学生的认知水平，同时也满足学生的知识构成的顺序要求，有效地突破了教学难点.

四、捕捉最佳提问时机

设置问题的时机是有效提问的保证.教师要敏锐地捕捉设置问题的最佳时机.比如在新旧知识产生矛盾冲突时设置悬念，促进知识技能的全面整合.

例如浙教版七年级上册第五章第一节《一元一次方程》的教学，首先让学生欣赏一个小学二年级的问题：老师的年龄和你的年龄之和是42岁，老师的年龄和你的年龄之差是18岁，请问老师几岁，你几岁？

紧接着，迅速跟进第二题，让同学们欣赏一个初中八年级的问题：我们教室这块黑板板面的长比宽长3米，其面积为6平方米，请问黑板面长多少米？

本节课作为章节起始课，要遵从概念的生成和发展过程，在已有知识的基础上，产生思维的冲撞.在教学过程中我们会发现，即使已经学习了方程，但是很多学生仍然喜欢用算式去解决问题，一方面是形成了算式的习惯，另一方面他们并没有认识到方程模型对于实际问题的适切性和优越性，因此教师应当设置问题让他们感受到方程带来的优势.

数学课堂是由问题构成的，问题是学生逻辑思维的起点.教师应该致力于帮助学生的思维从低阶的识记、理解、运用到高阶的分析、评价和创造.不同层次的学生有不同的思维提升需求和提升空间，好的课堂应该能够帮助每个学生都获得思维的提升.一堂优质课应该是重点突出高阶思维，教师应将学生的识记操作类学习转向理解性的学习，最后到主动探索性学习，真正意义上提升学生思维层级.