融合“三学”立足学情 促进生成——以“平行四边形的判定”教学设计改进为例

闫艳艳

(甘肃省兰州市第七十八中学(中国科学院兰州分院中学) 730000)

新课程背景下，初中数学教学力求实现学生主动建构知识、发展学生学力、促进学生学习方式转变.2017年起，我校开始进行李庾南“自学·议论·引导教学法”与 “导学自主”课堂相融合的研究.一次笔者应邀上了一节二者相融合的公开课，课题为北师大版《义务教育教科书数学》八年级下册第六章第二节“平行四边形的判定”.由于第一次教学设计缺乏对所教授学生学情的准确判断，试教时效果不佳.课后笔者在与教研组老师研讨分析后，仔细研究分析学生的学情，对教学设计的定位、教法、学法、渗透的数学思想等方面进行了认真反思与改进，改进后的教学设计立足于学情、关注了学生已有的数学知识和活动经验，在公开课上收到了较好的教学效果.现将设计的改进做以回顾分析.

一、教学设计的改进分析

1.回顾平行四边形的性质

原设计请同学们思考平行四边形有什么性质呢?发现相当一部分学生只能回答上一两条性质，缺乏对性质的全面理解与把握，没有条理性，因此该设计没有真正达到复习旧知，为学习新知做好准备和铺垫的目的.

改进问题1：组成四边形的基本元素有哪些？

问题2：如图，请你结合图形思考平行四边形是如何定义的呢？其性质是什么呢？

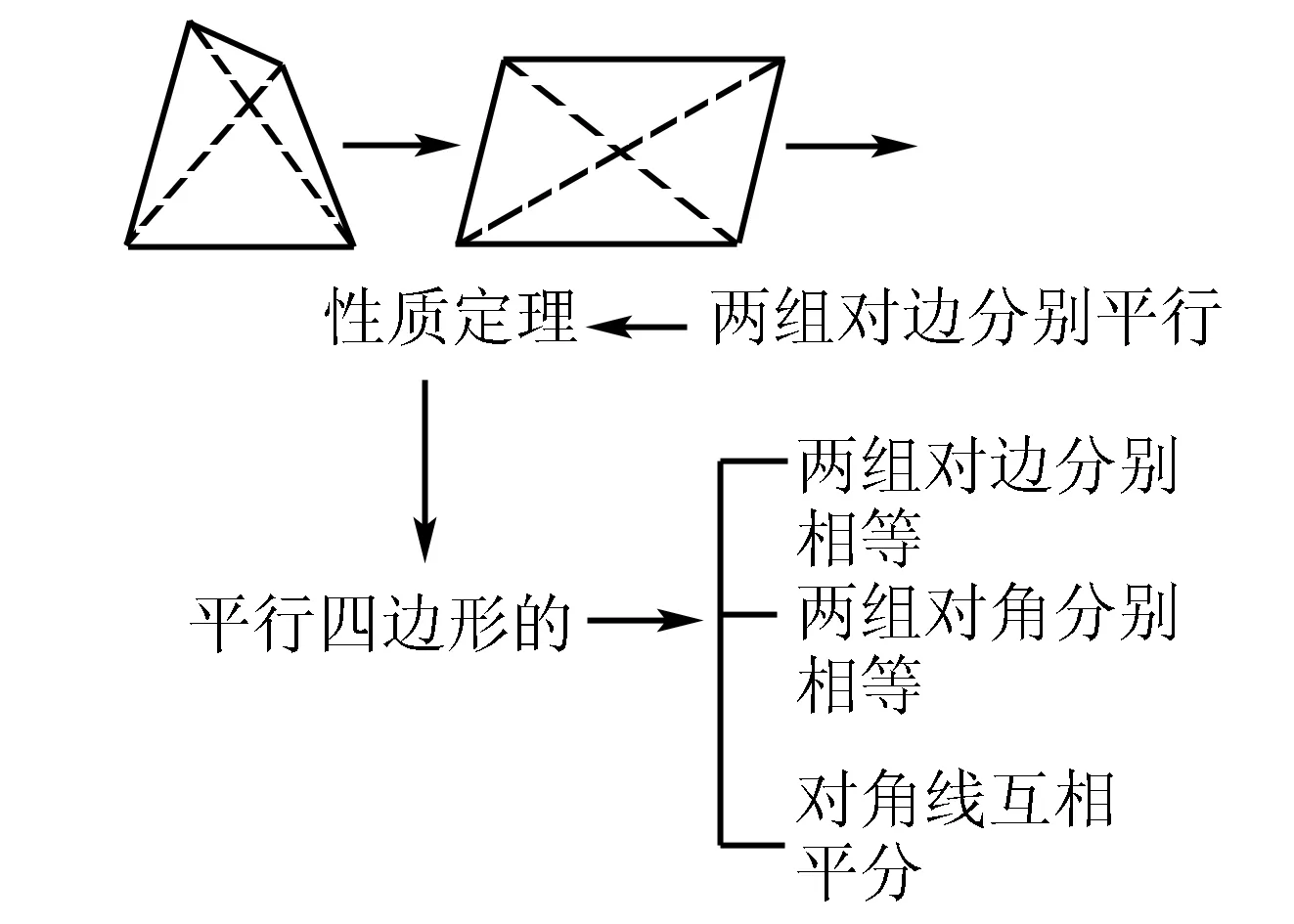
引导学生从“边、角、对角线”三个方面回顾平行四边形的性质定理，明确几何学习关键是文字语言、图形语言、符号语言之间的相互转化，生成如下的板书：

问题3：能否类比性质定理的研究，推导出平行四边形的其他判定方法呢？(揭示课题——平行四边形的判定).

对比分析改进后的教学设计基于学情，借助图形，更具体直观的引导学生分析问题，回顾旧知.设计中关注了知识之间的结构关系，渗透数形结合思想，既让学生对所学知识一目了然，又为研究新知提供了方向，做好了铺垫，还让学生感受到数学的结构美，统一美.

2.探究平行四边形的判定

原设计步骤一：在四边形ABCD中，具备了怎样的条件，就能推证到四边形的两组对边分别平行，进而根据定义去判定平行四边形呢？(数形结合)

在四边形ABCD中

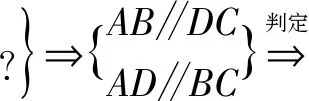
步骤二：学生小组讨论，自主探究平行四边形的其它的判定命题.

步骤三：全班交流各组提出的猜想

步骤四：全班研讨证明命题

课堂上一开始的问题就难倒了多数学生，他们一脸茫然，无所适从.原因是该环节的设计高估了学生的思维能力、学习水平，知识跨度较大，超出了学生实际的认知水平.

改进活动1：实践操作，探索新知

学生从准备好的小木棒中(至少有两组是等长的)挑出四根来，摆成平行四边形，思考：这四根木棒怎么挑？你能发现什么结论？说说你的理由.

活动2：互逆入手，生成新知

问题4：比较 “两组对边分别相等的四边形是平行四边形”与其性质定理，你有什么发现？

问题5：你能写出平行四边形的判定命题吗？如何证明？

对比分析该环节将深层次的思维活动调整为由浅层次的实践操作入手，让学生进行最直接的参与，最直观的感受，激发学生学习兴趣.再从学生已有的知识和学习经验出发，设计活动2，唤醒学生的记忆，引发思维深度.学生在充分独立思考的基础上，参与小组讨论，全班学习，新知在生生互动、师生互动中自然生成.事实上，这样有层次的、循序渐进的思维推进让每个学生都有不同层次的收获，能充分调动每一个学生的学习积极性，打破了原有课堂气氛的沉闷，有效地提高了课堂教学效率.

3.师生合作，建构知识、方法体系

原设计根据环节2的研究，逐条写出学生们猜想的命题， 等引导学生经历“画图—用符号语言写出已知、求证—分析证明思路—写出证明过程(选派代表板书)”这一严格的证明过程后，类比平行四边形的性质，从“边、角、对角线”三个方面归纳平行四边形的判定方法.

平行四边形的判定

角——定理：两组对角分别相等的四边形是平行四边形

对角线——定理：对角线互相平分的四边形是平行四边形

这样的归纳，新旧知识之间的联系体现得不够，忽略了数学知识的整体性，不能达到对数学知识的深刻理解.

改进：

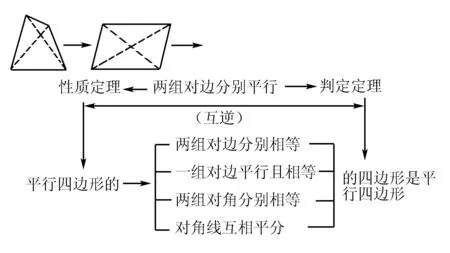
对比分析改进后的结构化板书，不仅使得新知的习得一目了然，还示范、传递出几何图形研究的套路，即定义、性质与判定.不仅明确了新旧知识之间的联系，还自然而然地感受到“互逆”“数形结合”“归纳”等数学思想，体现了数学的本质、过程、思想和结构，也让学生感受到数学的整体美、结构美，涵育数学核心素养.

二、几点思考

1.融合“三学”要立足学情

融合“三学”首先是“学材再建构”的实践与应用.“学材再建构”必须立足学情，对教学内容进行适度整合，才能真正实现优化学习资源.本案例在引导学生探索“平行四边形的判定”时，教材分两个课时进行探究，都创设了木条摆放的问题情境，笔者感到这样的设计与 “平行四边形的性质”关联不大，甚至“平行四边形的判定”也有被割裂之感.但第一次的“学材再建构”没有准确分析学情，一味追求了思维的深度，忽略了学生学习的层次性，知识之间的联系性，结构设计也没有很好体现.再次改进时，立足学情，先动手操作，再观察发现回忆“互逆”思想，然后引导学生自主探究平行四边形的判定，这样渐次深入的思考，使得新知的生成水到渠成.后续的试课证明，这样的设计我们学生的学情，贴近学生的最近发展区，顺应了学生思维发展的规律，教学效果明显.

2.融合“三学”要促进生成

“自学·议论·引导”教学法与“导学自主”的课堂，都倡导学生在自我学习、相互议论、互相补充中自主建构与探究知识、生成能力、智慧学习.原课例的设计，学生有些问题摸不清头脑，独立自学无从谈起，知识的自然生成被阻断，该内容的思维研究价值也被损害.改进后的课例，由一般四边形到平行四边形，数形结合，结构化的整理出“研究套路”：定义、性质、判定，而判定与性质又常常是“互逆”的，激活了学生原有的学习经验，促进了新知的生成，这个过程中学生不仅获得了一个新的知识、解决了一类新的问题，还学会了研究图形的基本套路，下次再碰到新的图形如矩形、菱形、圆等时，就会从定义、性质与判定的角度来展开自主研究，又可以从互逆的角度完善研究、扩大成果.这样设计使学生体会到 “数学的学习方式”即经历“明确研究对象——确定研究内容(判定)——构建知识体系”这三大步骤，辅之严格的推理，最终达到学生对研究对象的立体化认识，于是学生学力得以发展，学习智慧受到启迪，“教是为了不教”的目标才能逐步实现.