浅析初中数学教学中如何渗透数形结合思想

张少伟

(江苏省昆山国际学校 215300)

一、以概念教学为平台渗透数形结合思想

概念教学的本质是思维教学，是对于事物的本质属性加以观察、分析、抽象、概括、总结的过程，是人类认知的“高阶”形态.因此，在初中数学教学中，概念教学往往既是重点，又是难点.在传统数学教学中，很多教师习惯于让学生通过死记硬背的方式学习概念，显然难以取得良好的教学效果.相反，如果教师能够以教学教学为平台巧妙渗透数形结合思想，则能够帮助学生将抽象的语言叙述转变成直观的图形或真实的事物，从而帮助学生降低概念理解的难度、提高概念学习的效率.

例如，在学习“平面直角坐标系”的时候，如果教师直接对于“平面直角坐标系”的概念进行语言阐述，则学生对于“数轴”、“公共原点”、“象限”等知识点势必难以在短时间内做到消化和理解，对于“平面直角坐标系”的内涵也难以做到全面而精准的把握.相反，如果教师能够利用数形结合思想，进行以下教学设计，则能够取得良好的教学效果：首先，教师带领学生玩“沙场点兵”的游戏——教师将班级座位中心的学生的座位号定为0号，然后以0号为基准，通过“上三左四”、“下二右五”等指令，要求对应的同学起立；其次，教师将“0号同学”所在的排和列画在黑板上，标为x轴和y轴，然后，沿着x轴和y轴标上数字；再次，要求学生轮流到黑板上标出自己的座位在图形中对应的位置，并利用x轴和y轴上所标的数字，确定自己的座位号；最后，教师要求学生阅读教材中“平面直角坐标系”的概念，并将概念中的知识点与黑板上的图形一一对应.与此同时，尝试利用“平面直角坐标系”准确表述自己的座位号.如此一来，教师成功将书中抽象的文字通过数形结合的方式直观的展现出来，从而使学生能够迅速掌握“平面直角坐标系”的相关知识点，并理解“平面直角坐标系”的概念、内涵及作用，大大提高了教学效率，同时，渗透了数形结合思想.

二、以定理推导为平台渗透数形结合思想

定理推导，向来是初中数学教学的“重头戏”.通过定理推导，不仅能够让学生掌握定理的由来和用途，也能够让学生理解该定理中蕴含的数学思想和数学方法，使学生不仅“知其然”，更“知其所以然”，从而促进学生数学思维的发展和数学能力的形成.因此，在初中数学教学中，教师应该善于利用定理推导的机会，渗透数形结合思想.

例如，在学习《勾股定理》的时候，教师可以首先向学生展示毕达哥拉斯的“地砖图”，让学生通过观察“地砖图”，发现直角三角形的三边的数量关系；其次，向学生展示“勾股定理”推导过程中经典的“正方形叠加图”，让学生探究等腰直角三角形的三边的数量关系；最后，向学生展示“赵爽弦图”，让学生根据“赵爽弦图”，尝试推导直角三角形三边的数量关系公式，并通过“分割法”和“整体计算法”验证自己的推导结果是否正确.在上述教学过程中，教师先通过“以形表数”的方式，让学生通过观察图形，确定数量关系，再通过“以数表形”的方式，利用数量关系表达图形内涵，不仅使学生通过自己的独立思考完成了“勾股定理”的推导与验证，也实现了数形结合思想的渗透.

三、以运算教学为平台渗透数形结合思想

与小学数学不同，初中数学中的运算教学已经不单纯考查的是数字之间的加、减、乘、除等基本运算法则，而是考查学生对于逻辑关系和数学方法的发现、理解与应用能力，运算难度更高、强度更大.而这恰好为数形结合思想的渗透提供了平台，使教师可以引导学生在运算过程中尝试通过数字来展示图形，通过图形来表达数字，实现数形结合.

例如，在解3/x>x+2这个不等式的时候，如果学生采用“试值法”，显然运算量过大，难以真正求得解；如果学生直接求解，很多学生容易默认为x>0，导致所求结果的取值范围出现错误；即使有的同学想到了采用“分类讨论法”，将不等式分成x>0和x<0两种情况，也往往因为计算疏漏出现错误.此时，教师可以向学生渗透“数形结合”的概念，要求学生将不等式运算问题转化成“数轴”问题：设y1=3/x，y2=x+2，并画出两个等式对应的函数图象.在此基础上，尝试求取双曲线与直线的交点坐标，并通过观察和判断两个函数的图象关系，来求解不等式.在上述解题步骤中，教师成功将抽象的“数字”问题转化成了直观的“图形”问题，学生通过观察图形，所求结果一目了然，跃然纸上，成功避免了“试值法”运算量过大、直接求解取值范围错误以及“分类讨论法”运算失误等诸多问题，不仅快速而准确的解答了问题，也渗透了实现了数形结合思想的渗透.

四、以应用题教学为平台渗透数形结合思想

所谓应用题，通常指的是将含有数量关系的数学问题或生活问题以文字叙述或图形、表格等方式表达出来的数学题.对于初中生来说，解答应用题之所以比较困难，主要源于以下几点原因：1.理解能力较弱，对于语言叙述较长、逻辑关系较乱的题目难以准确提炼有效信息并做出正确理解；2.抽象思维较弱，难以发现所给题目中隐藏较深的数量关系；3.逻辑思维较弱，对于解题步骤较多的题目难以理清思路；4.运算能力较弱，容易在复杂运算中出现失误.初中生面临的以上问题，既给教师的应用题教学带来了困扰，也为数形结合思想的渗透提供了契机，教师可以尝试以应用题教学为平台，渗透数形结合思想.

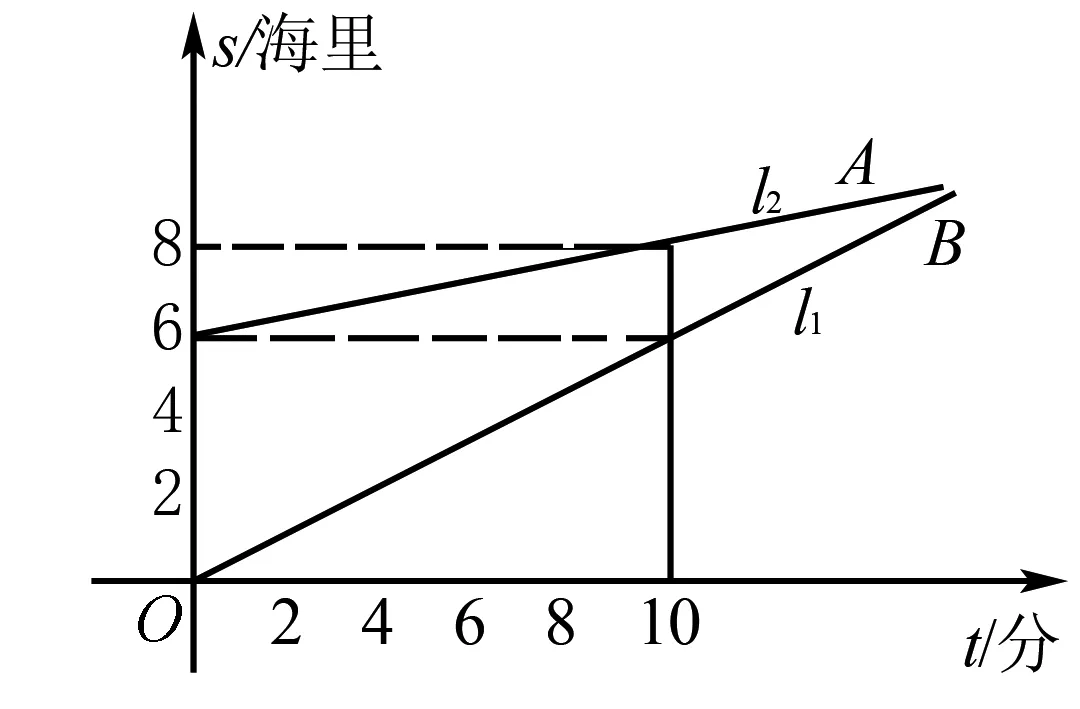
例如，下面的习题是初中数学中典型的“类型题”：有A和B两艘轮船同向行驶.在下图中，l2和l1分别表示的是A和B两艘轮船距离目的地的距离s与彼此之间追赶时间t的关系.现在，请同学们根据图片内容计算，当t的数值为多少的时候，轮船B能够追赶上轮船A.

一般来说，应用题的主要信息都隐含在文字叙述当中，学生需要通过剖析文字内容来准确的找到数量关系，列出算式并求解，从而得出答案.然而，当学生阅读本题的时候会发现，从文字叙述中只能获得最基本的提示，而单纯观察图片又无法发现潜在的数字关系.此时，教师就可以引导学生利用数形结合的思想，尝试列出l1和l2的函数表达式，将文字问题和图形问题转化成数字问题，并通过列出函数方程式并成功求解来获取答案.在这道应用题中，如果学生能够正确应用数形结合思想，就会迅速形成解题思路和解题方案，轻松求解.相反，如果学生不具备数形结合思想，就会始终不得要领，难以得出答案.因此，在讲解这道应用题的时候，教师应该着重强调数形结合思想的应用技巧，实现数形结合思想的渗透、促进学生数学思维和数学方法的形成.

五、以分类讨论为平台渗透数形结合思想

分类讨论，既是一种数学思想，又是一种数学方法，是初中数学教学中常见的教学内容.在传统数学教学中，很多教师没有认识到“分类讨论”中蕴含的渗透数形结合思想的良机，错失了很多机会.事实上，初中数学教师应该把握分类讨论的机会，将“分类讨论”与“数形结合”整合起来，促进学生数学思维的形成与发展.

例如，在学习《一次函数》的时候，教师的“常规操作”是让学生通过小组讨论理解一次函数y=kx+b(k≠0)中常数k的值与图象之间的对应关系.这显然是一个“数形结合”问题.同时，教师还可以针对这一问题进行进一步的“深度挖掘”，鼓励学生针对k>0和k<0这两种情况展开分类讨论并完成下面的表格：

教师通过对于“常规”问题的“深度挖掘”，将“常规”问题演变成了“分类讨论”和“数形结合”问题，不仅使学生学会“以形代数”和“以数代形”，还使学生学会了“数形互换”，使学生在更加全面、准确而深刻了解“一次函数”的变化规律的同时，对于“数形结合思想”有了更加深刻的理解和全面的把握.