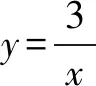巧用“特殊与一般思想”进行初三数学客观题解法教学
林振德
(福建省厦门市五显中学 361100)
2018年《福建省初中学科教学与考试指导意见》指出,数学基本思想着重考查学生对函数与方程思想、数形结合思想、分类与整合思想、特殊与一般思想、化归与转化思想、或然与必然思想等的领悟程度.在数学研究中,由特殊到一般,由一般到特殊的研究数学问题的思想,就是数学研究中的“特殊与一般思想”.
用“特殊与一般思想”解题的理论依据是“一般包含特殊,特殊属于一般”,其解题思路如下:
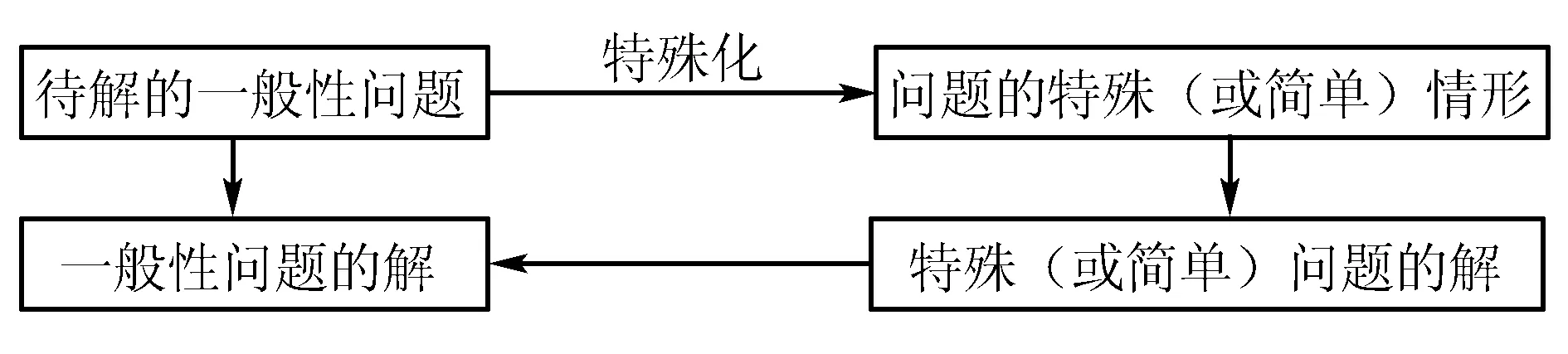
因此,对于判断型客观题,要检验一般性结论是否成立,只要验证特殊情况是否满足一般性结论要求即可判断结论是否正确.对于求值型(含化简或求值)客观题,在变量允许的取值范围内,可对变量取特殊值处理.本文重点选取近年来福建省、厦门市、部分省外中考试题及《福建省初中学科教学与考试指导意见》中的题型示例,向大家介绍“特殊与一般思想”在初三数学客观题解法教学中的妙用,期望收到抛砖引玉的效果.
一、字母类选择题,可对字母赋特殊值求解
例1如图,数轴上P、Q两点分别表示实数a、b,则下列结论正确的是( ).
A.a+b>0 B.ab>0 C.a-b>0 D.|a|-|b|>0
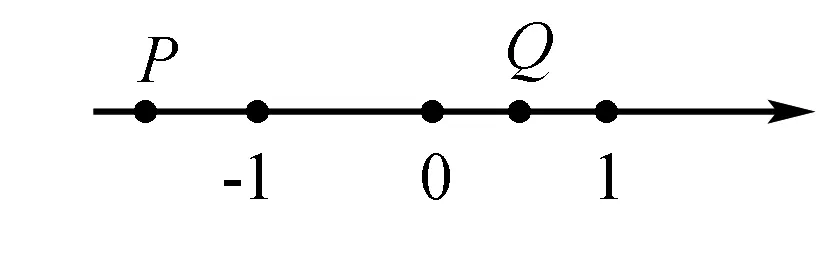
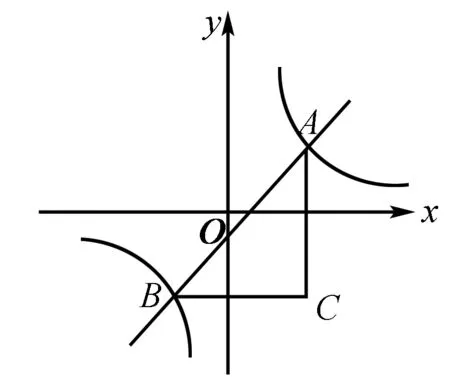
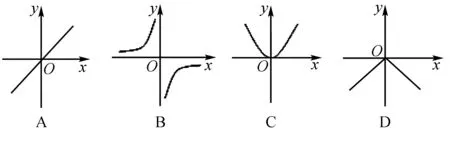
一般解法:观察数轴,得出a<-1,0 特殊解法:由图知,a<-1,0 结论1对于根据图形(数轴、直线、抛物线等)判断含参代数式符号的客观题,可在参数允许范围内,取特殊点(如交点、顶点、对称轴、中间点)进行验证. 例2(2017年福建4)化简(2x)2的结果是( ). A.x4B.2x2C.4x2D.4x 一般解法:(2x)2=4x2.故选C. 特殊解法:代特殊值验证.取x=1,先淘汰A、B;取x= -1,淘汰D . 结论2对于化简问题,因属恒等变形,一般可代入特殊值进行验证取舍. 例3(2017年福建9)若直线y=kx+k+1经过点(m,n+3)和(m+1,2n-1),且0 A.3 B.4 C.5 D.6 一般解法: 特殊解法:由0 结论3对于含多个参数的问题,应考虑从受限的参数出发,对其取特殊值,转化为验证点坐标是否满足函数方程问题. 例4(2016年福州11)已知点A(-1,m),B(1,m),C( 2,m+1)在同一个函数图象上,这个函数图象可以是( ). 一般解法:因为A(-1,m),B( 1,m)两点关于y轴对称,由右侧的B(1,m),C(2,m+1)两点可知,y随x的增大而增大,所以只能选C . 特殊解法:取m=1,画出A、B、C三点,对比选项中的图象,发现最接近C. 结论4对于含参数的图象判断(定性)问题,可通过对参数取特殊值,找到对应函数模型. 例5(2018年福建10)已知关于x的一元二次方程(a+1)x2+2bx+(a+1)=0有两个相等的实数根,下列判断正确的是( ). A.1一定不是关于x的方程x2+bx+a=0的根 B.0一定不是关于x的方程x2+bx+a=0的根 C.1和-1都是关于x的方程x2+bx+a=0的根 D.1和-1不都是关于x的方程x2+bx+a=0的根 一般解法:根据方程有两个相等的实数根可得出Δ=0,进而得出b=a+1或b=-(a+1).当b=a+1时,-1是方程x2+bx+a=0的根;当b= -(a+1)时,1是方程x2+bx+a=0的根.再结合a+1≠-(a+1),可得出1和-1不都是关于x的方程x2+bx+a=0的根.故选D. 特殊解法:通过观察,联想到常见方程x2+2x+1=0(或x2-2x+1=0),均满足Δ=0.由此可知,对于方程(a+1)x2+2bx+(a+1)=0,当a=0,b=1(或-1)时,均符合题意.此时,方程x2+bx+a=0可化为x2+x=0(或x2-x=0),其一根为0,另一根为1(或-1),选项A、B、C错,选D. 结论5对于一元二次方程的根的情况,在求出Δ,得出参数满足的条件后,通过观察,发现题设成立的特定条件(a=0,b=1或-1),分别代入选项求解即可. 结论6对于特定曲线上的动点有关的面积问题,可根据其限制条件,进行赋值. 结论7求双曲线与特殊直线(斜率固定)的交点与平行于坐标轴的直线围成的直角三角形面积最值时,可结合中心对称、面积公式、勾股定理,转化为交点弦长问题,通过观察图形,利用直线通过特殊点时的特殊方程进行求解. 教学启示:由上述例子,我们可以看到,数学思想是处理数学客观题的指导思想,而“特殊与一般思想”是帮助我们从多角度思考问题,灵活、快速、准确解答数学客观题的关键.我们教师在日常教学尤其是试卷评讲时,应该关注思想的渗透 ,避免就题论题,应该注重方法、题型的归纳,达到“举一反三、熟练应用、提升素养”的目的,确实提高初三复习效率,提升教学成绩.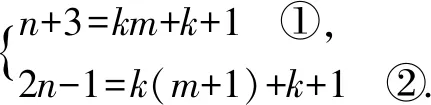
二、判断型或探索条件型的问题用特殊值断定
三、“任意点”问题作特殊化处理