立足基础 提升能力 引导教学——“面积法的运用与面积处理”的教学设计与简析

潘 宇

(江苏省苏州工业园区唯亭学校 215121)

一、基本情况分析

《不忘初心，方得始终——面积法的运用与面积处理》是初三数学专题研讨课.这节课中，老师立足基础，围绕面积处理问题，提炼方法，巩固方法，应用方法.梯度设计合理，思辨空间丰富，学生的解答过程能够体现出不同层次的数学品质、素养和习惯.

课题：面积处理：等积变形与图形的割补

二、教学过程

【方法提炼】如图1，如何求出△ABC的面积？

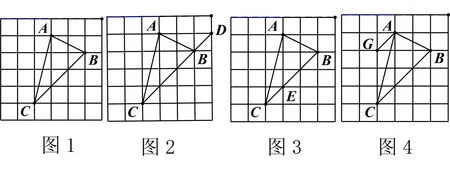
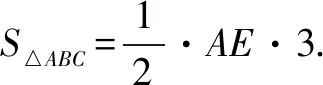
师：同学们还能想到别的方法么？如果大家都想不出来了，请大家看图4，思考为什么可以这么转换？

生2：在网格中发现AG∥BC,而两条平行线间的距离处处相等，由此我们可以知道S△ABC=S△BCG

师：回答得真好，我们把这些计算面积的方法进行一下总结.

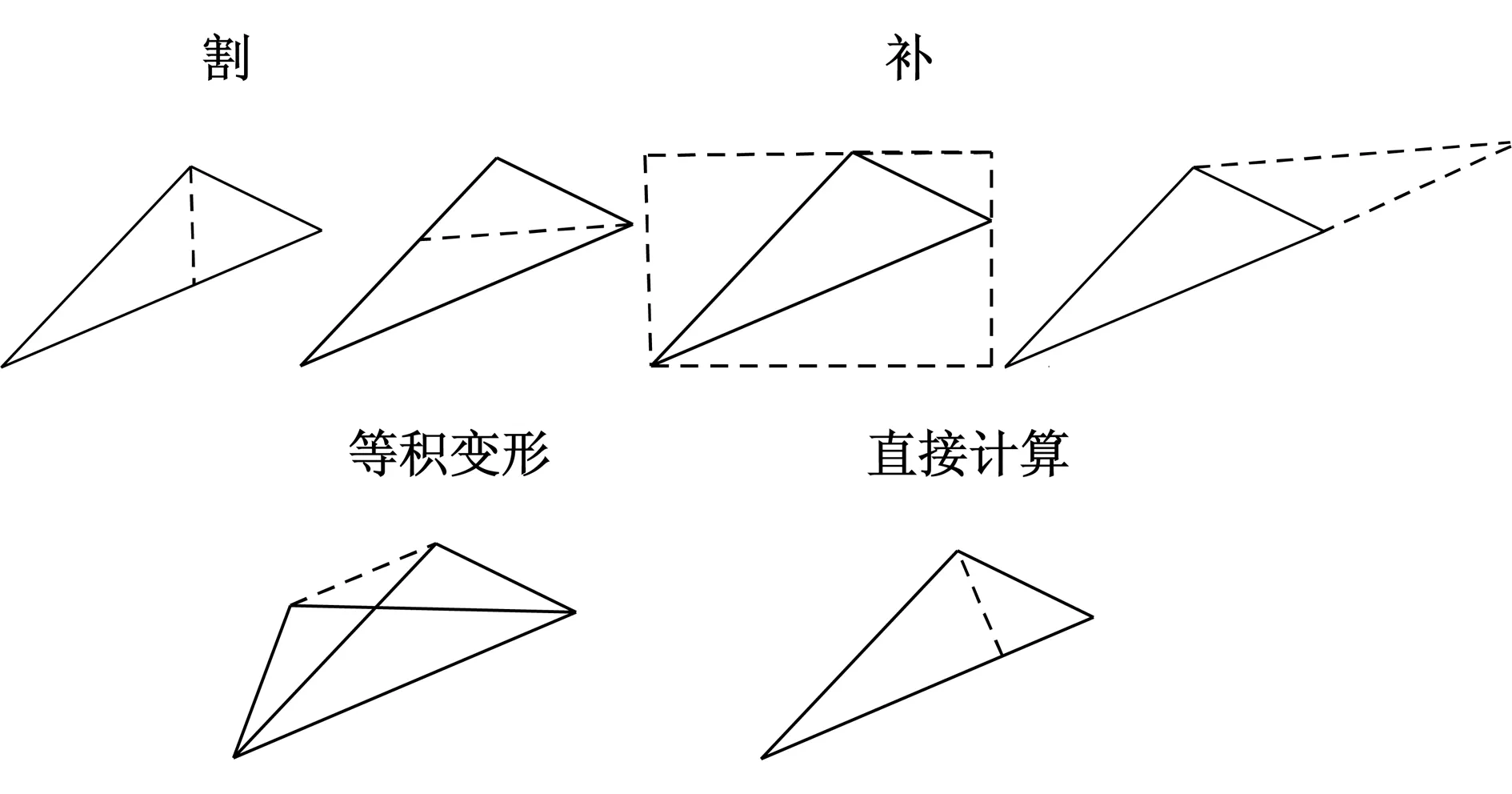
【教学价值简要分析】从网格中的求三角形面积入手，让学生易上手，并且学生能找到多种方法解决该问题.这个设计符合学生的认知能力，低起点、易上手、立足基础.初中阶段数学中的核心知识点是形成数学能力的重要载体和抓手，教与学只有立足基础，夯实基础，才能循序渐进，不断进步.

【方法巩固】1.如图5，求四边形ABCD的面积.

师：请同学们在学习单上画出求面积的各种方法.

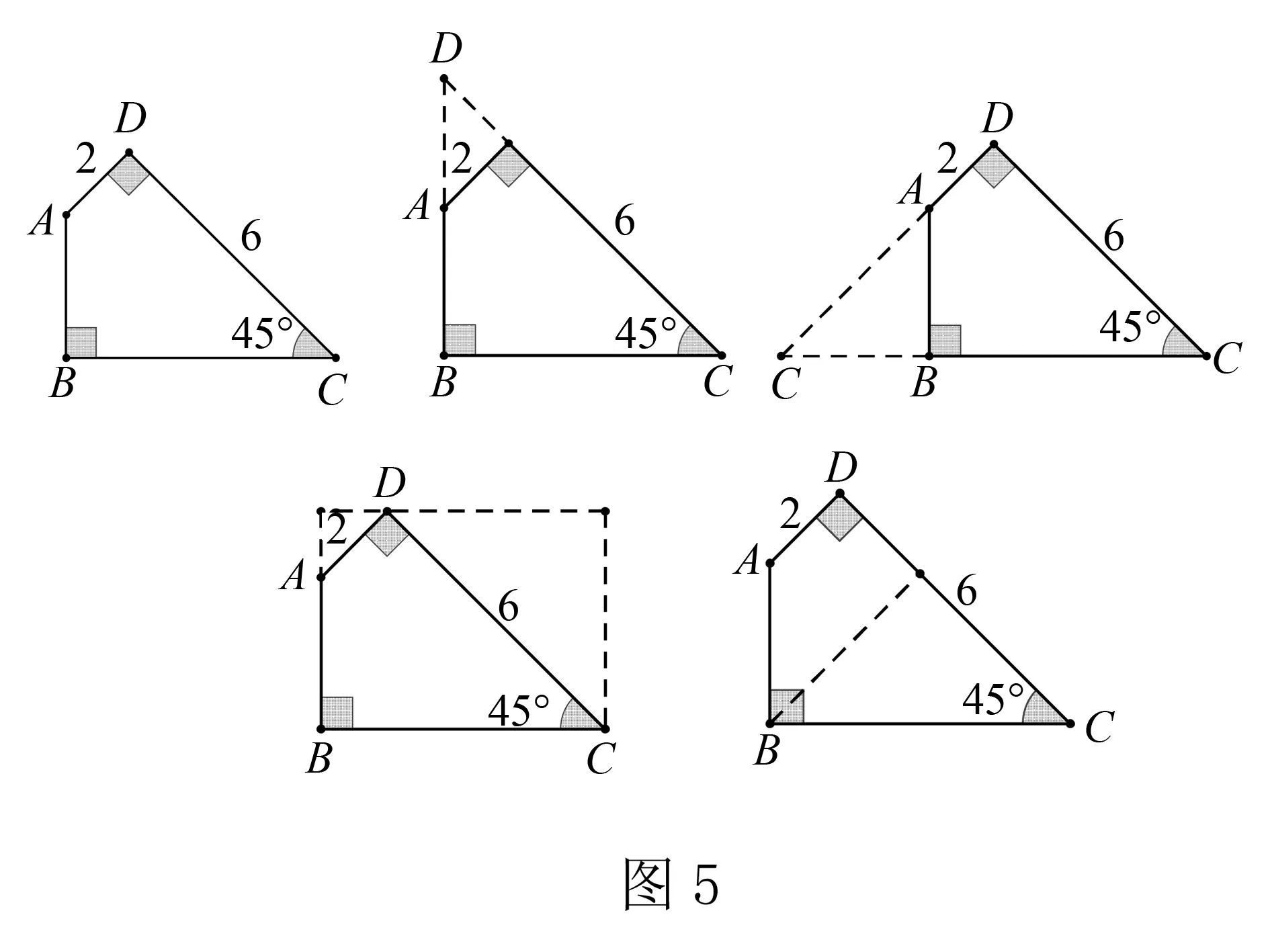
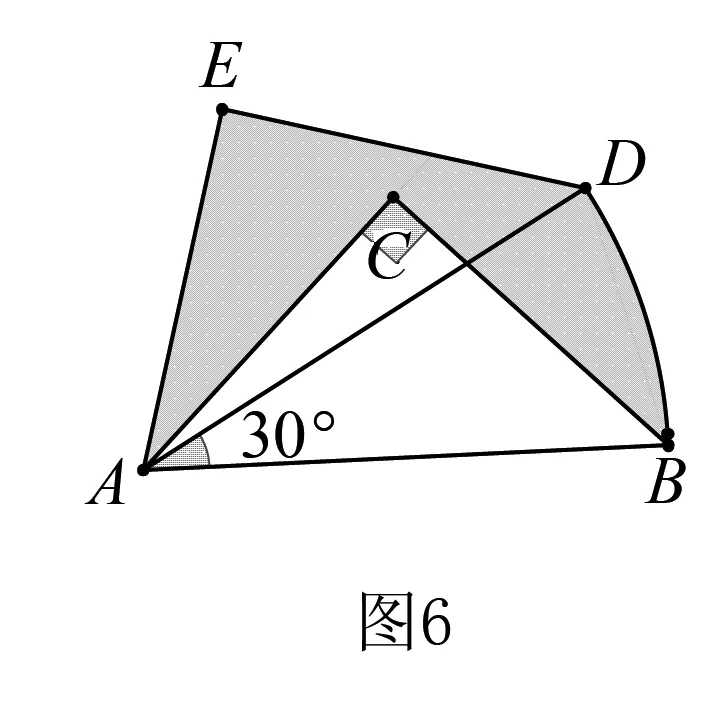
2．如图6，把△ABC绕着点A逆时针旋转30°得到△ADE,如何求阴影部分的面积？

生3：我们发现S=S△AED+S扇形ABD-S△ABC=S扇形ABD.

【教学价值简要分析】这两题在求面积问题上学生充分利用了割补法和等积变形法.数学思想方法是数学的精髓和灵魂，是学生将知识转化成能力的手段，所以在平时的教学中要逐步渗透，让学生在解题中反思，领悟.

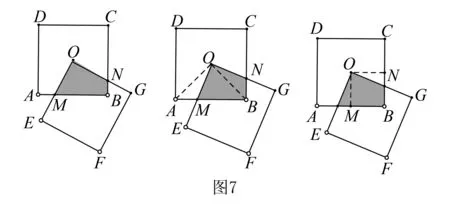
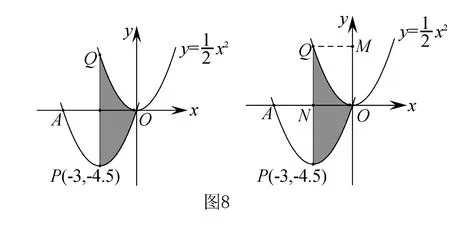
【方法运用】如图7、图8求阴影部分面积.

生4：对于图7，通过等积变形我们把阴影部分的面积转化为△AOB的面积或者正方形OMBN的面积.

生5：对于图8，过点Q作QM⊥y轴，我们可以得到阴影部分的面积等于矩形QMON的面积.

【教学价值简要分析】图7的这道题在八年级新授课中就已经接触过，在九年级的复习课中再次提出回顾，让学生把前后知识点能连贯起来，找到一类题的解题思路和方法.数学学习不能单纯依赖记忆和模仿，而要感悟与思考,所以我们要重视培养学生的探究能力，重视概念、方法教学，使学生在学习过程中理解、巩固、应用和拓展新知.

【解决问题】(2015年徐州中考题改编)如图，在平面直角坐标系中，点A(10,0)，点E(6,3)抛物线经过O、E、A三点.

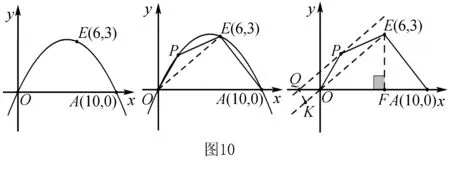
(1)求抛物线的函数表达式；

(2)若P为抛物线上位于第一象限内的一个动点，以P、O、A、E为顶点的四边形面积为16时，求点P的横坐标.

师：如何求△POE的面积？

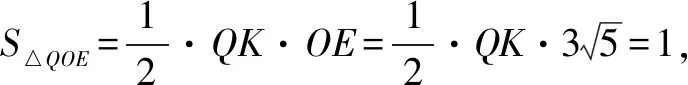
师：回答很棒!在理解了本节课的方法后能熟练应用，这就是我们这节课要达到的目标.

【教学价值简要分析】这道中考改编题第二问难度较大，但只要抓住该题的核心内容-面积，我们就可以利用求面积的方法去解决.在掌握了基本知识方法后，通过不断思考，去感悟知识的本质，积累思维和实践经验.要关注学生在解题过程中如何获得解题思路，关注科学本质，感悟数学的认知结构.

三、设计特点

这是一节初三专题课的教学设计.本节课，教师不是以学生会解题为目标，而是以一道题为载体，通过对这道题的研究，得出一类题型的解题思路，从而引导学生会研究数学问题的一般方法.从基础出发，由浅入深，让学生总结计算面积的几类方法，并能及时巩固运用，最后链接中考，让学生在此基础上能灵活应用方法解决问题.教学中就应该让学生经历知识的建构过程，突出对数学本质的认识和理解，做一个会探索的智慧人.