非线性砰击载荷对某大外飘型船舶疲劳损伤的影响

徐志亭，赵超，王福花

中国船舶及海洋工程设计研究院，上海200011

0 引 言

船体在海上航行过程中，受波浪的作用，船体会进行六自由度运动，导致船体结构产生变形。一般情况下，船体受到的波浪载荷和结构中的应力应变随时间的变化是一个缓慢、随机、与波浪特征一致的过程。当船舶航行于较高海况时，船体艏、艉部可能存在频繁地出水、入水的过程，在此过程中，会发生严重的砰击现象，给船体结构带来局部和整体的高频振动响应，也即颤振。颤振可加剧船体结构的疲劳损伤［1］。砰击现象一般发生在中、高浪级情况下，对于大外飘型船舶，由砰击弯矩造成的疲劳损伤不可忽略。因此，本文将针对由非线性砰击载荷造成的疲劳损伤问题进行研究。

目前，针对疲劳分析的直接计算法主要有谱分析法和设计波法［2］，通常不考虑非线性载荷的影响。在船舶力学研究与结构设计领域，越来越多的学者开始关注如何计算非线性波浪载荷，以及砰击非线性载荷成分对船体结构强度的影响，尤其是对一些具有大外飘、高航速等特点的船型［3］。进行船体结构疲劳强度校核时，采用时域计算能很好地计入非线性因素的影响，计算的波浪载荷时历能够较真实地反映出船舶航行时的状况［4］。因为需要求解船体振动响应，而将船体看作刚体来求解水动力问题的传统方法已行不通，必须引入水弹性理论。Wu 等［5］提出了三维非线性水弹性理论，以及二阶水动力作用，考虑了航速和定常兴波的影响，以及大幅度运动和瞬时湿表面变化等对非线性波浪力的贡献。综合来看，对由非线性砰击载荷造成的疲劳损伤，目前的分析方法都是先通过时域载荷理论计算非线性载荷时历，求得疲劳热点应力时历，然后再通过雨流计数法统计应力损伤次数，最后结合疲劳损伤累积理论计算疲劳损伤。但考虑到疲劳热点众多，计算工况复杂，载荷时历计算与雨流计数法费时费力，倘若能直接给出一个基于线性载荷的放大系数，便可极大简化计算过程。

针对上述问题，本文将首先针对船舯区域主甲板或底部纵骨，采用非线性时域水弹性方法计算非线性载荷（含砰击载荷）作用下的纵骨应力时历（该时历包含低频分量（线性成分）和高频分量（非线性成分））；然后，采用雨流计数法统计出纵骨节点在线性载荷和总载荷下的疲劳应力范围分布；接着，分别计算纵骨节点在线性载荷和总载荷下的疲劳损伤，并给出非线性砰击载荷产生的疲劳损伤放大系数；最后，将损伤放大系数转化为由砰击弯矩引起的等效波浪弯矩放大系数，由此，即可在计算全船其他节点的疲劳损伤时将波浪弯矩放大系数考虑进去。

1 时域非线性水弹性力学运动方程

在时域内，不规则波船体运动的非线性水弹性力学方程可以写为如下形式［6-7］：

或者

式中：a，b，c分别为船体的广义质量、阻尼和刚度矩阵；μ，B，C分别为流体的无穷大附加质量、考虑航速效应的阻尼及流体的回复力刚度矩阵；C′ 为考虑航速效应的刚度矩阵；Krs(t)为延迟函数，其可体现不规则波中的记忆效应；FI(t)为入射波力；FD(t)为绕射波力；FR(t)为辐射力；Fslam(t)为由船体剧烈运动引起的砰击力；FS(t)为静水回复力；pr(t)为t时刻第r 阶模态的主坐标；τ为积分变量。

为求解船体结构的运动方程，需要确定作用在弹性船体上的非线性流体载荷。

1）静水回复力［2］。

式中：ρ为流体密度；g为重力加速度；S(t)为瞬时湿表面；psa为主坐标；ur为弹性结构体的第r阶自由振动模态产生的位移矢量；n为垂直于物面方向的单位矢量；ws为第s 阶模态的垂向位移；FG为船体重力；Crs为第s 阶模态的垂向位移产生的静水动压力对第r 阶运动模态的贡献。

2）入射波力［8］。

根据卡明斯脉冲响应给出的时域波浪力卷积关系，船体的入射波力FI(t)可表示为

其中

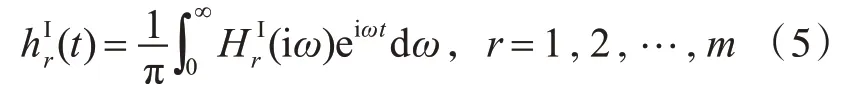
式中：ζ(τ)为不规则波波面起伏，m；(t)为第r 阶模态下波浪入射力的脉冲响应函数；(iω)为单位波幅规则波作用于船体上产生的波浪入射力的频响函数；ω为波频。

3）绕射波力［8］。

与入射波力的求解方法相同，不规则波中船体绕射力FD(t)的表达式为

其中，

为求解船体结构的运动方程，需要确定作用在弹性船体上的非线性流体载荷。

4）辐射力。

时域辐射力FRrs( )t的表达可分为瞬时项与记忆项相加的形式：

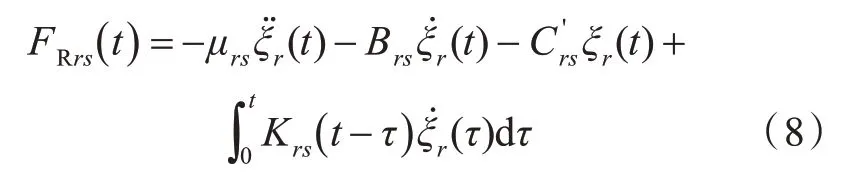
其中，

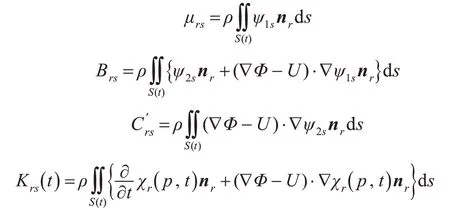
式中：S(t)为平均湿表面；nr为第r 阶模态单位法向矢量；Φ为定常速度势；U为船舶航速；ξr(t)为t 时刻第r 阶模态的运动位移，可用主坐标pr(t)表示；ψ1s为船舶在s 阶模态以无穷大频率运动时的流场速度势；ψ2s为与定常移动有关的速度势；χr(p，t)为 自 由 面 的 记 忆 效 应。ψ1s，ψ2s和χr(p，t)满足的初边值问题在这里不予展开，具体细节参见文献［9］。

5）砰击力。

根据动量砰击理论［1］，当船体与波浪的相对速度大于0 时，在任意时刻t，船体所受砰击力Ff(t)为

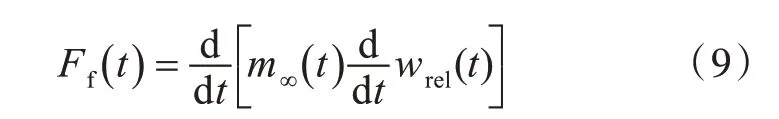
式中：m∞(t)为频率趋于无穷大时的垂荡附加质量；wrel(t)为船体表面点P(xb，yb，zb)与波浪的垂向相对位移，表达式为

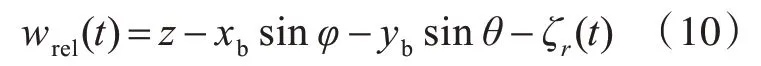
式中：z为重心处的垂荡响应；φ为重心处的纵摇响应；θ为重心处的横摇响应；ζr(t)为规则波的波面升高，其表达式为

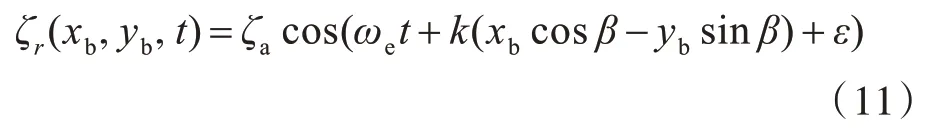
其中，ζa为规则波波幅；k为规则波波数；ωe为遭遇频率；β为航向角；ε为初始相位。

当考虑了船体在流场中的弹性变形后，船体与波浪的垂向相对位移的表达式为

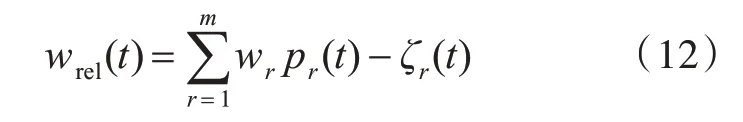
式中，wr为第r 阶模态的垂向位移。对应的垂向相对速度为

此时，加入到船体振动方程的砰击作用力可以写为如下形式：

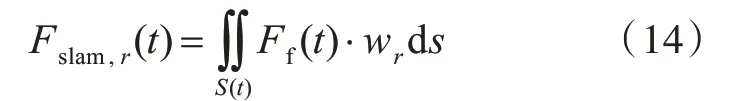
6）自动舵力。

由于船舶的水平运动不具有恢复力，故带来了斜浪求解发散问题。但在实际情况下，在波浪中航行的船舶是通过不断操舵来保持自身航向和航迹的，而引入自动舵模型后，可以解决水平运动求解发散问题。

式中：BRudder为摇艏和横荡运动阻尼系数矩阵；CRudder为恢复力系数矩阵；ERudder为积分项系数矩阵；η为只含船舶横荡和艏摇的运动矩阵；η̇为只含船舶横荡和艏摇的运动速度矩阵；η6为船舶的艏摇运动。详见文献［6］。

7）时域非线性水弹性力学方程的求解［8］。

时域非线性水弹性力学方程通常采用四阶龙格—库塔（Runge-Kutta）法求解。Runge-Kutta 法为显式单步法。经典的Runge-Kutta 法具有4 阶精度，对于初值问题：

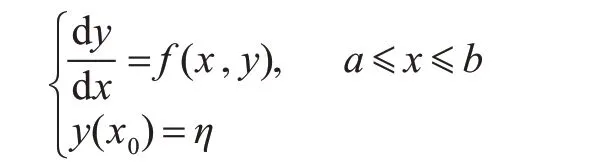
其步进求解的格式为：

式中：f(x，y)为变量y对变量x的导数；xn，yn为第n 次循环后的x值和y值；l 为时间间隔；K1～K4为求解的参数。

给定初值，对于上述标准一阶微分方程组用Runge-Kutta法步进求解，即可获得运动响应时历。

解出主坐标后，利用模态叠加原理，就可以得到船体结构的位移w(x，t)、弯矩M(x，t)和剪切力V(x，t)［6］。

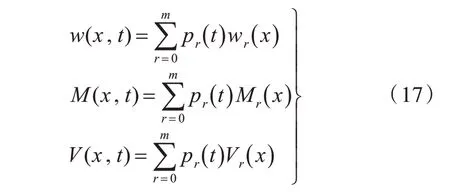
式中，Mr，Vr分别表示第r阶模态的弯矩和剪切力。

2 考虑非线性砰击载荷影响的船舶结构疲劳评估方法

船舶结构疲劳强度评估方法一般包含2 个方向：一个是建立S-N 曲线以及Miner 线性损伤理论的累计损伤判定方法；另一个是基于断裂力学的计算方法。本文主要采用第1 种评估方式。疲劳强度评估的直接计算方法主要包含以下内容：作用在船体结构上的疲劳载荷计算，其中涉及水动力分析、应力响应评估和疲劳损伤计算。

发生砰击时，除了由砰击引起的颤振效应，还存在高频波激振动效应，本文的非线性时域水弹性分析方法包含两者的影响。

非线性砰击载荷（含高频波激成分）计算都是在时域范围内进行，故得到的应力响应都是时历响应。其可以通过雨流计数法进行统计分析，得到不同砰击载荷的循环次数，进而再进行疲劳损伤计算。具体计算步骤为：

1）基于三维非线性时域分析方法，计算船体梁垂向波浪弯矩的时历。此波浪弯矩包含低频和高频分量，其中，低频分量为不含砰击振动影响的垂向波浪弯矩（即波频分量），高频分量为波激振动和砰击颤振诱导的垂向波浪弯矩。

2）分别将垂向波浪弯矩波频分量和总弯矩的时历响应作用在船体上，得到计算点在波频分量作用下的应力时历和总弯矩作用下的应力时历。

3）采用雨流计数法［10］对应力时历进行计数统计，获得各装载工况、海况和浪向下各个波频分量的应力范围Sw，k，或各个总弯矩应力范围St，k的循环次数。

结合S-N 曲线和Miner 线性累积损伤准理论，分别按式（18）和式（19）获得单位时间内第n 装载工况、第j 海况和第i 浪向角的波频分量疲劳损伤度dnji，w与总弯矩疲劳损伤度dnji，t。

波频分量疲劳损伤度：

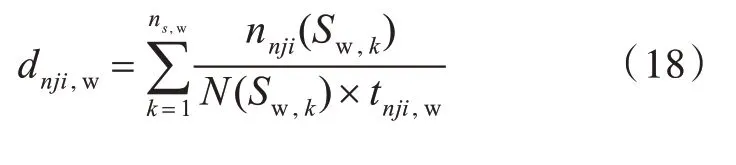
总弯矩疲劳损伤度：

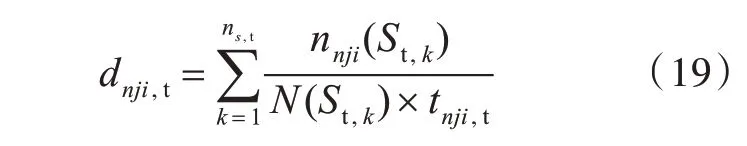
式中：nnji(Sw，k)，nnji(St，k)分别为第n 装载工况、第j 海 况、第i 浪 向 角 条 件 下 第k 个 应 力 范 围Sw，k和St，k的 循 环 次 数；N(Sw，k) ，N(St，k) 分 别 为 根 据S-N 曲线获得的对应于应力范围Sw，k和St，k的疲劳 失 效 循 环 次 数；tnji，w，tnji，t分 别 为 第n 装 载 工况、第j海况、第i 浪向角条件下波频分量载荷和总弯矩载荷的拟合时间，s；ns，w为第n 装载工况、第j海况、第i 浪向角条件下波频分量应力范围的个数；ns，t为第n 装载工况、第j海况、第i 浪向角条件下总应力范围。

计算点处波频分量的疲劳累积损伤度由式（20）得到。

式中：nl，ns，nh分别为装载工况总数、海况总数、浪向总数；T 为损伤计算总时间；pn，pj，pi分别为第n装载工况、第j海况、第i浪向的发生概率。

计算点处总弯矩分量的疲劳累积损伤度按式（21）获得：

4）计算由砰击弯矩引起的疲劳损伤放大系数。

砰击载荷引起的疲劳损伤放大系数可由下式获得。

由于大部分计算点的疲劳损伤受船体梁载荷和局部载荷的双重影响，而此影响系数主要考虑了船体梁砰击弯矩对疲劳损伤的影响，未考虑局部砰击载荷对疲劳损伤的影响，故适用于由船体梁总纵弯曲引起的疲劳损伤计算。

5）计算由砰击弯矩引起的等效波浪弯矩放大系数。

在常规计算点的疲劳强度评估中，一般分别计算船体梁载荷和局部载荷，船体梁载荷一般仅计入线性波浪载荷（近似于波浪弯矩的波频分量），因由非线性高频砰击载荷引起的疲劳损伤计算费时费力。倘若将由高频砰击弯矩引起的疲劳损伤放大系数转化为等效波浪弯矩放大系数，可以采用低频波浪弯矩线性放大的简化方法快速评估任一计算点的总纵弯曲疲劳损伤，以及由总体载荷和局部载荷引起的总疲劳损伤。

在船舶结构疲劳分析中，经常采用两参数的Weibull 分布来表示应力范围S的长期分布，且假定S-N 曲线最常用的形式是幂函数式［5］，即

式中：N为与应力范围S相对应的疲劳结构失效次数；m和A为与材料、应力比、加载方式等有关的S-N 曲线参数。

则相应的疲劳损伤计算式［11］为

式中：NL为所考虑的整个时间期间内应力范围的总循环次数；q为应力范围长期分布的尺度参数，q=S0/(lnN0)1/h，其中S0为超越概率水平为1/N0的应力范围；h为应力范围长期分布的形状参数；Γ()为伽玛函数。

由于应力范围与波浪弯矩成正比，则由砰击弯矩引起的等效波浪弯矩放大系数kp为

式中，m为S-N 曲线反斜率。

3 算例计算

本文以某大外飘型船（船长约200 m）为例，进行含砰击载荷影响的疲劳损伤计算。

选取北大西洋海浪散布图，海浪的功率谱密度函数采用由有义波高HS和平均跨零周期TZ表征的双参数P-M 谱。浪向角取为0°～360°，浪向角间隔为30°，各浪向角的发生概率相等。按照满载工况、50%在航率，计算25年时间内的疲劳损伤。

计算位置选取为受船体梁弯矩影响的船舯剖面甲板纵骨和外底纵骨。本文将线性载荷时历和非线性载荷时历分别施加在有限元模型上，通过有限元应力状态分析，得到热点应力范围。全船有限元模型如图1 所示。

图1 全船有限元模型Fig.1 FE model of the whole ship

按照前文所述，对不规则波中垂向弯矩的时历进行计算。分别对波频分量的疲劳损伤、考虑砰击载荷影响的总弯矩疲劳损伤进行计算，计算结果如表1 和表2 所示。

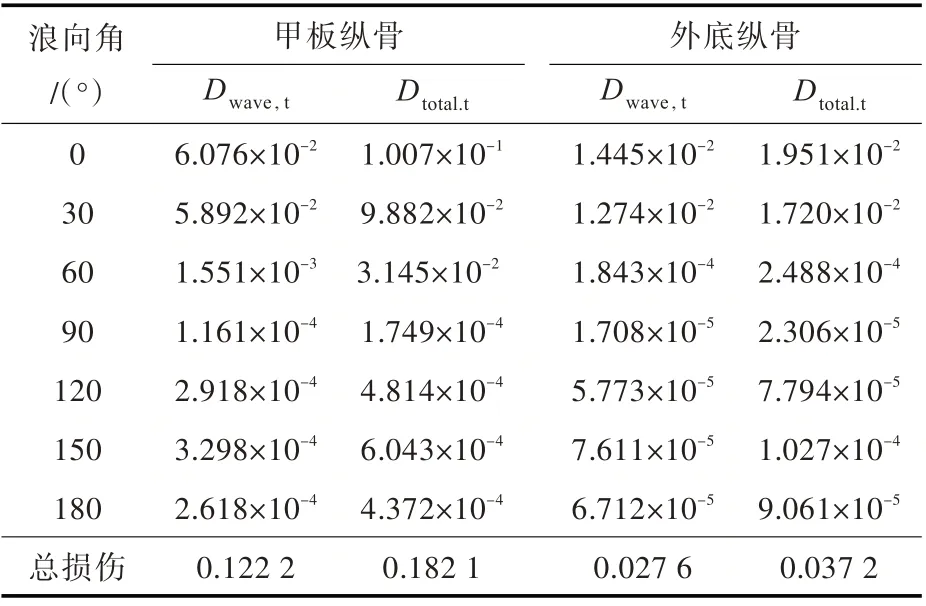
表1 船舯剖面纵骨疲劳校核结果Table 1 The check results of longitudinal fatigue damage in midship section

表2 船舯剖面砰击弯矩放大系数Table 2 The amplification coefficients of slamming moment in midship section

由计算结果可以看出，考虑砰击载荷影响后，与波频分量疲劳损伤相比，由总弯矩引起的疲劳损伤较大；同时，甲板纵骨与外底纵骨处的放大系数不同。取所有测点中放大系数的最大值，可使结果偏于保守，因此，将目标船砰击载荷对船体梁载荷的放大系数取为1.142。此系数可对本船其他节点处的波浪弯矩进行修正。

在不同浪向工况计算中，可以发现对疲劳总损伤贡献最大的工况出现在迎浪或艏斜浪（30°），绝大部分疲劳损伤的贡献来自艏斜浪（60°以内）。

4 结 语

本文介绍了考虑非线性砰击载荷影响的船舶结构疲劳评估方法：选用只受船体梁载荷的纵骨节点计算损伤放大系数和弯矩放大系数，然后在所有节点上修正船体梁载荷，但并不修正局部载荷，进而将修正后的船体梁载荷与未修正的局部载荷联合作用，求得了考虑砰击弯矩的疲劳损伤。不过，本文在以下方面还有进一步改进的空间：

1）本文选取的计算点较少，只在船舯剖面处选取了计算点，所得弯矩放大系数只反映了船舯砰击弯矩的影响。考虑到砰击弯矩沿船长的分布并不一致，故弯矩放大系数沿船长也将是变化的。若沿船长方向取多个剖面的计算点，可以得到各个剖面的弯矩放大系数，进而总结砰击载荷放大系数沿船长方向的变化规律，从而能够更准确地反映出砰击弯矩的影响。

2）本文给出的砰击载荷船体梁放大系数是假定应力范围的长期分布为weibull 分布，且S-N曲线为单斜率幂函数形式，其他情况仍需进一步研究。

3）本文的计算方法可应用于砰击载荷严重的各种船型，针对同一船型的多艘目标船进行非线性砰击载荷影响研究后，可以总结归纳出该船型的砰击载荷放大系数，为同型后续船的设计工作提供支持。

4）本文方法适用于全船所有节点，适用于能将船体梁载荷和局部载荷分离的简化计算法、有限元直接计算法；但对于谱分析和设计波法，只适用于只受船体梁载荷的节点。

综上所述，本文所采用评估方法可以方便地应用于常规疲劳损伤计算方法中，对更准确地评估大外飘、高航速等遭受严重砰击载荷影响的船型的船体疲劳强度具有指导意义。