多工况下基于子模型的矿砂船舱口角隅形状尺寸耦合优化分析

陈雪，王德禹

上海交通大学船舶海洋与建筑工程学院，上海200240

0 引 言

货运船甲板设置的大开口破坏了甲板的纵向连续性，且开口角隅处几何形状的突变致使该处产生了较高的应力集中。因此，改善舱口角隅的应力集中成为研究者关注的重点。目前的研究主要集中在角隅的形状优化方面，即通过改变角隅的几何形状来实现应力集中系数的降低。

陈震等［1］对某船舶舱口角隅处结构强度进行了有限元细化分析，结果表明，细化分析后的结果远大于粗网格结构强度分析结果。俞铭华等［2］采用边界元法和带自适应移动界限的序列线性规划，对平面应力状态下的船舶甲板舱口角隅进行了形状优化，使舱口应力集中极小化，从而确定了舱口角隅的最佳形状。Okumoto 等［3］针对具有椭圆形角隅的方形甲板开口，采用有限元方法计算了其应力集中系数，并据此对某集装箱船的开口角隅进行了优化，但处理的工况简单且单一。高上地等［4］对矩形耐压舱角隅结构进行形状优化，得到了弧形加强角隅形状，通过对形状优化后的角隅结构进行拓扑优化，有效降低了角隅结构的应力集中，并获得了创新性的角隅结构型式。张干锋等［5］结合参数化建模和改进Kriging 近似模型，对某过渡肘板和舱口角隅边界进行了形状优化，在保证极小误差和缩小计算成本的情况下，得到了理想的应力分布和重量优化结果。可以看出，上述研究均是对舱口角隅进行形状优化，因而降低了船舶角隅结构的应力集中。

通过分析发现，舱口角隅应力集中问题除了和角隅肘板的形状关系密切之外，还和角隅肘板周边的结构有关，例如甲板纵桁、甲板横梁、舱口围板、舱口围肘板等。因此，本文将主要关注某矿砂船的舱口角隅应力集中问题，在对角隅肘板进行形状优化的同时，考虑角隅肘板与周边关联结构的耦合效应；通过提出一种适于优化的子模型选取方法和多工况筛选方法，以及灵敏度分析方法，最终实现矿砂船舱口角隅的形状尺寸耦合优化。

1 适于优化的子模型构造

1.1 子模型技术

针对船舶局部结构强度的分析通常有2 种：第1 种是直接将细化网格模型嵌入三舱段模型中进行局部强度分析，也即直接使用细化的三舱段模型进行局部强度分析；第2 种是采用子模型技术创建局部模型来代替原模型进行计算分析。

所谓子模型技术，是指从整体模型中截取一部分，并对局部关注区域网格予以细化，然后将整体模型分析的位移结果作为对应子模型的边界条件，并保留对应子模型上的外载荷，重新计算，从而得到更为精确的局部分析结果的一种技术。由于子模型可以在减小计算量的同时模拟结构的真实受力情况，所以在分析局部强度或者进行疲劳分析时，常使用子模型技术。对本文而言，第1 种方法虽然计算精确，但计算量较大，并不适合需要进行大量重复计算的优化问题。而子模型技术只需对局部模型进行分析，可以极大地减少计算时间，适于后续的优化分析。所以，本文选用子模型方法进行角隅局部强度分析和后续优化计算。

关于子模型技术，已有不少学者进行过相关研究。许允等［6］以散货船底边舱下折角的局部结构细化网格分析为例，分析了子模型范围、边界节点角位移约束、子模型新增节点的插值处理以及子模型边界节点所在位置对应力结果的影响。任慧龙等［7］通过有限元分析软件，建立了SWATH 船舷台与支柱体连接处过渡结构关键部位的参数化子模型，并进行了结构优化设计，在满足细网格屈服衡准的情况下降低了结构质量。程远胜等［8］通过子模型技术，对船舶肘板节点结构进行了应力精细化分析，并在此基础上对肘板进行拓扑优化，提出了一种新型的肘板结构形式，有效降低了节点应力集中。但在许多采用子模型进行优化的研究中，都只验证了子模型对强度分析的适用性，而并未验证其对于优化问题的适用性。

1.2 适于优化的子模型的选取与验证

子模型的边界选取与强度分析结果的准确性直接相关，因此，边界的选取通常需要进行多次尝试并予以验证。采用子模型方法时，子模型的最小范围为其边界对应于相邻主要支撑构件所在的位置［9］。本文中，角隅结构的形状和尺寸是随着优化迭代而不断变化的，如果切割边界较小，依据子模型原理，那么形状和尺寸的改变势必会对切割边界的位移产生较大影响，即原先加载在切割边界上的位移是不准确的，那么所得优化结果也是不可信的。因此，适于优化的子模型的切割边界应足够远离关注区域，以保证优化区域的形状尺寸改变后，子模型应力分析结果仍在需求的精度范围内。同时，适于优化的子模型的范围应尽可能小，以降低计算成本。

因此，本文截取了不同范围的子模型，首先验证子模型方法的正确性以及子模型本身的计算精度，然后，通过对比形状尺寸变化后角隅的最大应力是否与完整模型误差较小，来验证子模型是否适于优化，并提出适于优化的子模型选取方法。

1.2.1 子模型的构建

本文的研究对象为一艘250 kDWT 矿砂船。该船总长325 m，型深25 m，型宽57 m，设计吃水18 m，舱口长17.28 m，宽17 m。采用有限元软件Patran/Natran 建模并进行强度分析。图1 所示为该矿砂船的三舱段有限元模型。本文主要关注中间第5 货舱舱口角隅的应力集中，需对该角隅处进行细化网格有限元分析。原舱段模型的舱口区域为无角隅肘板的粗网格模型，需首先建立椭圆型角隅肘板模型。规范规定，当强力甲板上机炉舱、货舱开口的角隅是抛物线形或椭圆形时，椭圆长轴与舱口宽度之比不得小于1/10，椭圆短轴与舱口宽度之比不得小于1/20［10］，因此，本模型角隅的初始设计取为长轴1 700 mm，短轴850 mm。然后，采用50 mm×50 mm 的网格对角隅局部区域进行进行细化。最后，细网格区域内的所有板采用壳单元表示，并将纵骨一维梁单元替换为二维壳单元建模［9］，以保证能够真实反映实际结构的力学性能。图2 所示为细化网格前、后角隅局部模型。

图1 矿砂船舱段模型Fig.1 FE model of the ore carrier hold section

图2 细化网格前、后舱段模型Fig.2 FE model of the ship cabin before and after refining the mesh

本文选取了3 种子模型进行分析：子模型a 为最小范围的子模型，其边界横向对应于相邻的甲板横梁，纵向对应于相邻的甲板纵桁，其中多出支撑构件的1 个单元格仅为方便子模型边界位移加载，如图3（a）所示；子模型b 是在最小子模型区域的基础上向外延伸一个强构件间距，如图3（b）所示；子模型c 为截取的三框架模型，即模型范围内包含完整的三个横框架，如图3（c）所示。

图3 不同范围的子模型Fig.3 Different range of sub-models

本文选取满载轻货迎浪状态下的1_FULL_L_HSM1_SJ 载荷工况作为验证工况。首先，在初始设计下，从原模型分析的计算结果中输出该工况下对应子模型边界位置处的六自由度节点位移信息，然后，通过Pcl 命令语句将位移数据自动加载到子模型的边界节点上，同时保留子模型范围内相应的外载荷，以此作为子模型的边界条件和载荷。加载位移边界后的子模型b 如图4所示。其中，模型初始设计参数为1 700，850，42，27，12，15，12 mm，该数据从左到右分别为椭圆肘板长轴长a、椭圆肘板短轴长b、肘板及甲板厚度t1、甲板纵桁厚度t2、甲板横梁厚度t3、舱口围肘板厚度t4和舱口围板厚度t5。

图4 加载位移边界后的子模型bFig.4 Sub-model b after loading displacement boundaries

将3 个子模型角隅区域的最大中面应力与原模型的最大中面应力进行对比，结果显示，3 个子模型角隅区域的最大中面应力与原模型的一致，均为523 MPa，验证了子模型方法的正确性，同时也说明3 个子模型均适用于局部强度分析。原舱段模型和子模型的计算结果应力云图如图5所示。

1.2.2 适于优化的子模型的精度验证

通过设置2 组改变设计变量的实验，并对比其对子模型精度的影响，来筛选出用于后续优化的子模型。为有效验证，本文选取的2 组实验的设计变量分别为第3 节耦合优化设计变量的上、下限。

图5 初始尺寸下原模型和子模型应力云图Fig.5 Stress contours of original model and sub-models at original design

为有效验证，本文首先采用拉丁超立方抽样方法，从设计变量的设计域中抽取了20 个样本点，加上设计域的上、下限共计22 个样本点。然后，始终保持子模型边界条件和载荷为上节中的初始状态数值，分别计算子模型及原舱段模型在上述设计样本点下的最大应力。最后，以原舱段模型分析结果为准，比较子模型相对于原模型的误差，结果如表1 所示。其中设计变量下限为1 700，850，36，23，10，11 和11 mm，设计变量上限为3 350，1 850，48，31，14，19 和15 mm。

由表1 可以看出，随着切割边界的扩大，从子模型a 到子模型c，适于优化的精度越来越高。对于子模型a，其最大误差为9.3%，精度不足以用于优化。子模型b 的最大误差为4.7%，子模型c 的最大误差为2.9%，其误差均在合理范围内。这说明子模型b 和子模型c 的边界已较为远离优化区域，优化参数的改变对切割边界的位移响应影响较小，两者均可代替原模型进行优化计算。但与三框架子模型c 相比，角隅局部子模型b 的计算量明显减小，因此，选用子模型b 作为第3 节优化的模型。

由此，本文总结出适于优化迭代的子模型选取方法：首先，对子模型本身的应力计算精度进行验证，确认子模型的正确性；然后，通过改变子模型待优化参数，验证子模型切割边界是否远离优化区域。本文的结果表明，在最小子模型范围的基础上往外扩1～2 个强支撑构件距离，便可选出适于优化的子模型。

表1 改变厚度后舱段模型和子模型的结果对比Table 1 Comparison of the results of cabin model and sub-models after changing the thickness

2 矿砂船多工况的筛选

由于矿砂船需要在满载、非满载、压载、多港等多种工况下运营，如果每一种工况均参与优化迭代，会导致计算量过大，因此本文提出了一种工况筛选方法，并对矿砂船的56 个计算工况进行了筛选。考虑到角隅应力并非随设计参数的增大而呈线性变化，其在降低某一工况应力的同时可能提高其他工况的应力，因此，简单地根据应力大小排序对工况进行筛选是不可靠的。当角隅处于设计域上的应力最大状态，即各个工况的最大von-Mises 应力值为其在整个设计域上的应力最大值时，可通过判断工况的角隅最大应力是否超过许用应力来判别危险工况。

本节使用完整舱段模型进行工况筛选，其中，56 个载荷工况均依据《矿砂船船体结构强度直接计算指南》［9］加载。

首先，调整角隅处的设计变量参数，以使角隅处于设计域的应力最大状态。依据对带椭圆形角隅的矩形孔应力集中系数的研究结果［11-12］，在本文的设计域上，对形状变量角隅短轴取最小值，长轴取最大值时，角隅的应力集中最严重。同时，依据经验，构件厚度越小，应力越大。因此，对形状变量角隅短轴取最小值、长轴取最大值，对尺寸变量均取最小值时，角隅处于应力最大状态，即各设计变量取为3 350，850，36，23，10，11，11 mm，该设计变量代表的构件同1.2.1 节的初始设计参数。

其次，通过有限元计算筛选出超出许用应力的工况。本文角隅区域所用钢材屈服强度为355 MPa，材料系数为0.72，依据《矿砂船船体结构强度直接计算指南》［9］，细网格许用应力（单位：MPa）衡准应满足如下要求：

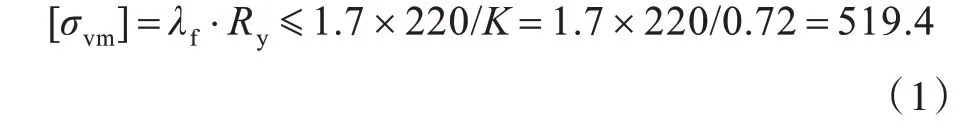
式中：λf为细化网格屈服利用因子；Ry为材料的屈服强度，Ry=220/K，MPa，其中K为材料系数，取为0.72。

通过计算，各工况在设计域上的最大von-Mises 应力值如图6 所示。

图6 各工况在设计域中的最大应力Fig.6 The max von-Mises of all subcases

由图6 可知，超出许用应力的工况共计8 个，具体如表2 所示。这些工况将被筛选出作为第3节的优化工况，从而可极大地缩短优化计算时间。

为验证本文所提工况筛选方法的可行性，即其是否能真正代替所有优化工况，需要在优化结束后，将优化后的设计变量代入计算，此时，所有工况的最大应力均小于许用应力即可。本文的验证结果将在3.3 节中描述。

3 矿砂船舱口角隅的形状尺寸耦合优化

在对舱口角隅进行优化设计时，一般工程上只关心角隅肘板的形状设计，却未考虑角隅周边邻接结构对角隅局部应力的影响。因此，本文提出了将角隅肘板的形状和尺寸，以及其周边结构尺寸同时进行耦合优化的方法。本节优化模型采用第1 节筛选出的子模型b，优化工况采用第2 节筛选出的工况，并采用Patran/Natran 和Isight 软件进行优化计算。

3.1 角隅形状尺寸耦合优化模型构建

从工程实际考虑，最优的角隅局部结构应不仅能够较好地减缓应力集中，同时还不能增加太多的质量。因此，本文优化的目标设置为在满足应力约束且结构质量增加较少的条件下，使角隅局部区域的应力最小化。对于多工况对应的多个应力，本文引入权重系数，将多目标问题简化为单目标问题。

表2 优化工况Table 2 Load cases for optimization

由此，该优化问题的数学模型如下：

式中：stress为各工况的加权应力，MPa；wj为各工况应力的权重；stressj为各工况的应力，MPa；xi为设计变量，包括形状设计变量和尺寸设计变量；ai和bi分别为各设计变量的上、下限，mm；[σvm]为材料的许用应力，MPa；mass为结构总质量，t；massobj为目标结构质量，t；i为设计变量序号；n为总设计变量数；j为工况序号；m为总载荷工况数。

针对该优化问题的求解，Sonmez［13］采用模拟退火算法对二维平面结构的形状进行了优化，使其在平面应力状态下的应力水平得到了显著优化；El Alem 等［14］采用自适应模拟退火算法对一个六边形板的形状进行了优化，使其在面内压应力作用下的应力水平得到了降低。因此，本文采用模拟退火算法求解该优化问题。

3.2 角隅的形状尺寸耦合优化

对于本文的矿砂船角隅优化问题，式（2）优化模型的参数选择如下：要求各工况的应力水平均优化到许用值以下，且整体应力水平越低越好。因此，目标函数中各个工况的应力权重值相同，均设置为wj=1。

设计变量xi包括形状设计变量和尺寸设计变量，其代表的结构如图7 所示，具体值如表3 所示。角隅肘板与甲板在实际工程中为一块加强板结构，故厚度一致。本文子模型区域的材料屈服强度均为355 MPa，由式（1），可知各工况下的许用应力均为519.4 MPa；本文约束的结构质量增加不超过原始质量的0.5%，即

式中，massini为结构初始质量，t。

图7 耦合优化的设计构件Fig.7 Design members of coupling optimization

表3 设计变量初始值及变化范围Table 3 The initial values and range of design variable

为便于比较，本文设置了2 组优化方案。其中方案1 为只对角隅肘板进行形状优化，方案2 为所有形状尺寸设计变量均进行优化。表4 显示了方案1 和方案2 的优化结果、其与初始设计的对比，以及两个方案结果的对比。

分析优化结果，发现方案2 耦合优化结果的各工况平均应力较规范设计降低了23%，最危险工况应力（工况23）较规范设计降低了19%，表明考虑角隅周边结构的形状尺寸耦合优化方法能够很好地降低舱口角隅的应力水平，提高结构安全性。且方案2 耦合优化结果各工况的平均应力较方案1 的降低了5.0%，最危险工况应力（工况23）较方案1 的降低了10.3%，表明在相同质量约束下，考虑角隅周边结构的耦合优化结果明显优于传统方法中只对角隅进行形状优化的结果。

3.3 考虑变量筛选的耦合优化

第2 节考虑了将所有角隅邻接结构作为设计变量进行优化的方案，但在极小化角隅应力的过程中，每个变量的影响程度并不一致，影响小的变量可以忽略掉，以节约计算成本和制造成本。因此，本节将对所有设计变量纳入优化的必要性进行了研究。通过实验设计（Design of Experiments，DOE），将7 个设计变量对所有优化工况平均应力和最大应力的影响进行灵敏度分析，所得结果如图8 所示。将7 个设计变量对子模型重量的影响进行灵敏度分析，所得结果如图9 所示。

由图8、图9 可以看出，a，b，t1，t3，t4对应力的影响比较明显，而t1，t2，t5则对质量的影响较大，由于本文优化目标为应力最小，故选取对应力影响较大的因素作为设计变量进行优化。以该设计变量组合作为方案3，其优化结果及对比如表5 所示。

由表5 可见，方案2 较方案3 的尺寸变量结果有一定的差异，t2和t5减小，t1增大。结合DOE 分析结果，这是由于t2与t5虽然对角隅应力的影响较小，但对结构质量的影响较大。因此，在优化过程中可以通过减小t2和t5，转移更多的质量来为t1提供更大的优化空间，同时降低应力水平。

但同时也可以看出，方案3 与方案2 的优化结果相比相差甚少，方案3 耦合优化结果的最大应力（工况23）较方案2 的仅高1.1%，平均应力仅高1.7%。由此说明，本文灵敏度筛选所得结果可靠。在矿砂船角隅耦合优化中，仅选择敏感结构肘板及甲板、甲板横梁、舱口围肘板进行优化，同样能取得理想的效果。该结论可为实际矿砂船角隅优化的变量选择提供参考。图10 所示为3 种方案的耦合优化结果汇总。

表4 两种方案耦合优化结果汇总及对比Table 4 Optimization results summary and comparison of two schemes

图8 对应力的灵敏度分析Fig.8 DOE analysis for stress

图9 质量灵敏度分析Fig.9 DOE analysis for total mass

将方案3 的优化设计结果代入原舱段模型，并计算所有载荷工况的应力，结果如图11 所示。由图可知，优化后，所有工况应力均在许用应力之下，证明本文第2 节所提多工况筛选方法可靠。

表5 优化结果汇总及对比Table 5 Summary and comparison of the optimization results

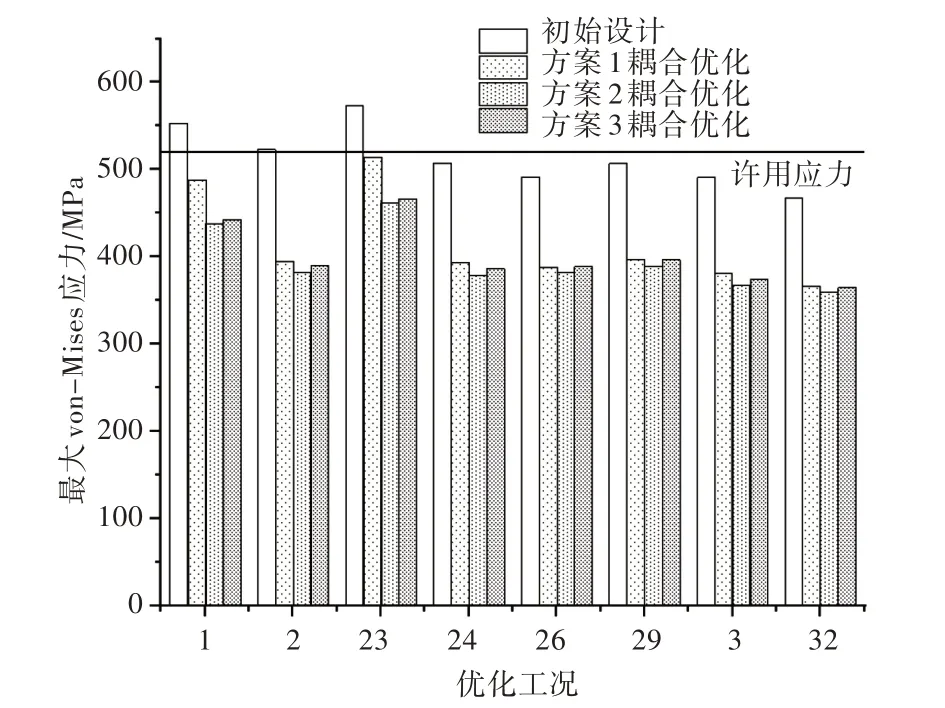
图10 3 种方案的优化结果对比图Fig.10 The optimization results comparison of the three schemes

图11 方案3 优化结果下各工况最大应力Fig.11 The max von-Mises stress of all subcases of scheme 3

4 结 语

本文通过子模型技术与工况筛选，减少了优化计算量；采用模拟退火算法对矿砂船舱口角隅进行形状尺寸耦合优化设计，降低了角隅的应力水平，提高了结构安全性。得到如下主要结论：

1）子模型区域内形状或尺寸参数的改变会对其精度造成影响，因此在选取子模型的范围时，需对子模型进行适于优化的验证。

2）通过计算各工况在设计域上的应力最大值是否超过许用应力，完成了多工况的筛选，该方法可大大减少矿砂船的优化工况，降低计算量。通过最终优化后的验证，证明该工况筛选方法可靠。

3）基于提出的形状尺寸耦合优化方法，有效降低了矿砂船角隅应力水平。相比初始设计，各工况的平均应力和最危险工况应力分别下降了23%和19%，与传统的只对角隅肘板形状进行优化相比，分别下降了5.0%与10.3%。

4）灵敏度分析结果表明，在对矿砂船角隅进行耦合优化时，肘板、甲板、甲板横梁、舱口围肘板对矿砂船角隅应力的影响较为显著，应选择这些结构作为设计变量，其可为实际矿砂船的角隅优化设计提供指导。

本文针对矿砂船提出的舱口角隅形状尺寸耦合优化方法以及设计变量筛选方法，也可为其他船舶的舱口角隅优化提供参考。