基于改进Bi-RRT 的无人水面艇自动避碰算法
欧阳子路,王鸿东*,王检耀,易宏
1 上海交通大学海洋工程国家重点实验室,上海200240 2 上海交通大学海洋智能装备与系统教育部重点实验室,上海200240
0 引 言
无人水面艇(USV)具有自主程度高、航速快、隐身性能好及机动性强等特点,被广泛应用在水文探测、海事巡航以及军事作战等领域。近年来,随着人工智能技术的再次兴起及自动驾驶技术的大规模应用,USV 作为智能技术与传统船舶学科交叉融合的产物,已成为国内外智能装备的研究热点之一。
自动避碰是USV 实现智能航行的关键技术之一,一定程度上反映了USV智能化水平的高低[1-2]。国内外许多学者在USV 避碰方面也取得了一定的研究成果。Svec 等[3]提出了3 种考虑风浪对USV艇体造成影响的规避障碍物方法,分别为:考虑障碍物边界进行路径规划;考虑外界环境的影响修正规划路径并再规划;将局部边界最优规划与启发式A*算法相结合并通过博弈树搜索位置。Kuwata 等[4]采用速度障碍法并结合国际海上避碰规则设计了USV 避碰方法,该方法在避碰过程中根据USV 操纵运动特性设置了最小转向角并考虑风浪流的影响。Benjamin 等[5]将行为控制框架原理、间隔规划等多重思想融入多目标区间优化方法中来解决USV 避碰问题。庄佳园等[6]考虑国际海上航行规则,将USV 碰撞分为追越、交叉相遇与正面相遇3 种局面,设计了一种符合国际海上航行规则的相对坐标系下动态规避方法,并搭建了USV 半实物仿真平台。吴博等[7]通过分析USV 与障碍物之间的相对速度和相对位置的角度关系,提出了一种基于速度障碍法并考虑风浪流影响的USV 操纵运动特性的自主避碰算法。张洋洋等[8]将速度障碍法和动态窗口法相结合,提出了一种无人水面艇动态避障算法。
从上述国内外研究情况来看,解决USV 避碰问题的主要思路可分为两类:一类是将其转化为局部路径规划问题并与智能算法相结合;另一类是基于速度障碍法得出避碰路径的可行范围。而目前将两者结合的研究成果较为少见。
受前人研究启发,本文拟将速度障碍法基本思想与已成功运用于Kinodynamic 路径规划问题[9]的双向搜索树(Bi-RRT)算法相结合,首先针对父节点延伸方向位于锥形碰撞区内的情况提出避碰危险度系数ω与障碍物排斥向量R,从而使搜索树向着远离障碍物的趋势延伸;然后提出一种两搜索树并行延伸的方法及当父节点延伸方向位于锥形碰撞区外时触发的目标吸引向量A,以提高算法的实时性并加强两搜索树朝目标点靠近的趋势;最后通过仿真实验证明改进算法的可行性与优越性。
1 无人水面艇避碰模型
USV 在自主航行过程中通过智能感知系统实时探测预定航线及其周边的障碍物,并自动规避障碍物。本文设定的USV 避碰问题如图1 所示,具体描述如下:t0时刻艇A 以速度V沿预定航线OS 航行,USV 智能感知系统感知到航线OS 以及周边出现此前未探测到的障碍物区域B1,B2,B3;以艇A 总长为直径作圆,所覆盖的区域视作该USV 区域。基于上述情况,本文基于改进Bi-RRT算法设计一种自动避碰算法,使艇A 尽量保留原定航线,在B2,B3的限制下安全、高效地规避B1。
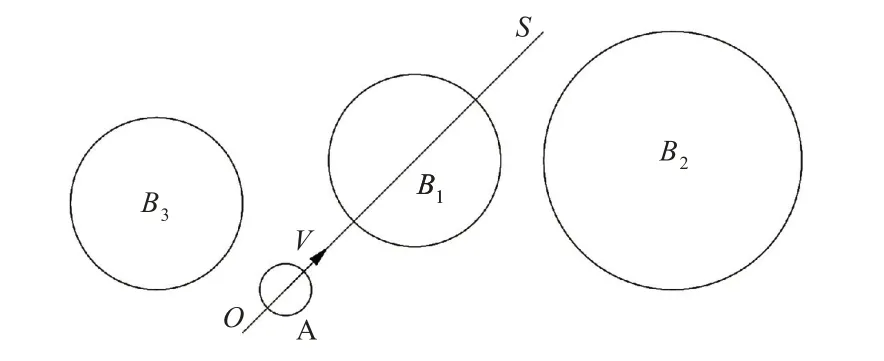
图1 USV 避碰情形Fig.1 The situation of USV collision avoidance
2 速度障碍法和Bi-RRT 算法
2.1 速度障碍法的原理
速度障碍法由Fiorini 等[10]提出,该方法的避碰原理为:首先,基于Featherstone 的理论,将任意多边形表示为相应的一系列圆,同时为了便于建模与计算,将USV 与障碍物分别用不同的二维圆形代替;然后,将USV 尺寸附加到障碍物尺寸上计算两者之间的速度障碍关系,从而将USV 简化为一个质点,使得障碍物区域膨胀为半径更大的圆形区域;最后,定义锥形碰撞区为USV 与障碍物发生碰撞的相对速度的集合,几何上表示为以USV为顶点向障碍物圆周作出的两条切线所夹的二维区域,而在锥形碰撞区以外区域中的相对速度将使USV 安全避碰。
速度障碍法为USV 避碰过程中如何改变和控制航向提供了简单高效的依据,也是Bi-RRT 算法在USV 避碰中运用及改进的理论依据。
2.2 Bi-RRT 算法
Bi-RRT 算法是La Valle 等[11]受双向搜索技术[12]的启发而提出。相比La Valle 于1998 年提出的经典快速扩展随机树(RRT)算法[12],Bi-RRT 算法分别以起点Xinit与终点Xgoal为根节点,构造两棵快速扩展随机树,两树同时生长,直到相遇为止。
Bi-RRT 算法由于保持了经典RRT 算法在状态空间中规划路径的思想,所以也保持了其优越性。La Valle[13]对RRT 算法分别进行了完整性约束、非完整性约束、Kinodynamic、闭式运动链条件下的路径规划测试,结果表明,该算法在处理具有微分约束的系统及单查询非完整性约束系统的路径规划问题上表现得非常高效。Bi-RRT 算法作为RRT 算法的改进,算法终止条件是以路径规划起点为根节点生长的搜索树与以路径规划终止点为根节点生长的搜索树相遇,理论上这可以提高对位姿空间搜索的效率;同时在该算法中,两树扩展节点的操作有着向对方搜索树靠近的趋势,理论上可以增强搜索的目的性,缩短路径规划时间。设两棵搜索树分别为Ta与Tb,搜索树Ta以USV 当前位置Xinit进行初始化,搜索树Tb以原始航线上的航迹恢复点Xgoal进行初始化。迭代过程中某搜索树T生成随机点Pr(Xr,Yr),T中离该随机点Pr最近的节点为Pp(Xp,Yp),Pp将作为该迭代过程中的父节点以USV 探索步长S向Pr进行延伸,延伸得到的子节点为Pn(Xn,Yn)。障碍物坐标为Po(Xo,Yo) ,障碍物膨胀半径为R。Bi-RRT 程序流程如图2 所示。
Bi-RRT 算法应用于USV 避碰时两棵搜索树分别以艇A 当前位置Xinit(X0,Y0)与预定航线OS上的航迹恢复点Xgoal(X1,Y1)为根节点,然后不断扩展节点直到两树满足相遇条件,最后通过两棵搜索树相遇点分别进行回溯操作,得到艇A 避碰路径点及完成路径规划。图3 所示为算法的构建过程。
3 Bi-RRT 算法的改进
基于速度障碍法,综合考虑USV 避碰的实际情况与算法本身的运行效率及实时性,针对搜索树延伸方式不利于智能规避障碍物以及父节点选取方式影响算法实时性的弊端,本文对Bi-RRT 算法进行了改进。
3.1 障碍物排斥向量R 的设计

图2 Bi-RRT 算法的程序流程图Fig.2 The execution procedure of Bi-RRT algorithm
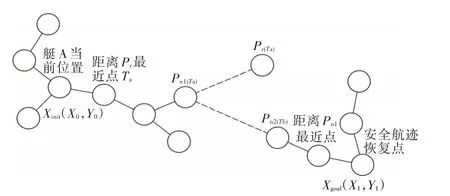
图3 Bi-RRT 算法的构建过程Fig.3 The build process of Bi-RRT algorithm
Bi-RRT 算法搜索树延伸方式为:先将一棵搜索树中距离位姿空间随机点最近的节点扩展至新节点,然后再扩展另一棵搜索树距离该新节点最近的节点。尽管该扩展方法理论上加强了两棵树延伸的目的性,但是若该随机点引导两棵搜索树同时向趋近障碍物方向发展,其表现在USV 避碰模型上则是该随机点引导USV 航向调整至锥形碰撞区,所带来的影响是轻则加大后续节点延伸标准步长后落至障碍物区域概率增大,加大算法的无谓消耗而重则使算法无法收敛和规划出有效的避碰路径。
鉴此,本文提出一种基于速度障碍法的障碍物排斥向量R,以改进Bi-RRT 算法的延伸步骤,改进后在迭代过程中能自动识别父节点延伸方向是否位于锥形碰撞区,并能根据避碰危险度系数ω动态调整R 的作用强度,使USV 避碰路径更加合理高效。
根据Bi-RRT 算法的延伸步骤,延伸子节点坐标Pn(Xn,Yn)为

采用向量表示式(1)为

若该次延伸操作使USV 航向引导至锥形碰撞区,即几何上满足α1<θ1,其中:

此时,将触发本文改进Bi-RRT 算法中R与ω,在R与ω作用下,延伸子节点Pn及其坐标不再满足式(1)和式(2),由过渡向量V 及向量表达式(8)得到:

式中,Ls为安全避碰临界距离。式(6)的核心函数为双曲正切函数y=tanh(x),该函数图像如图4所示。
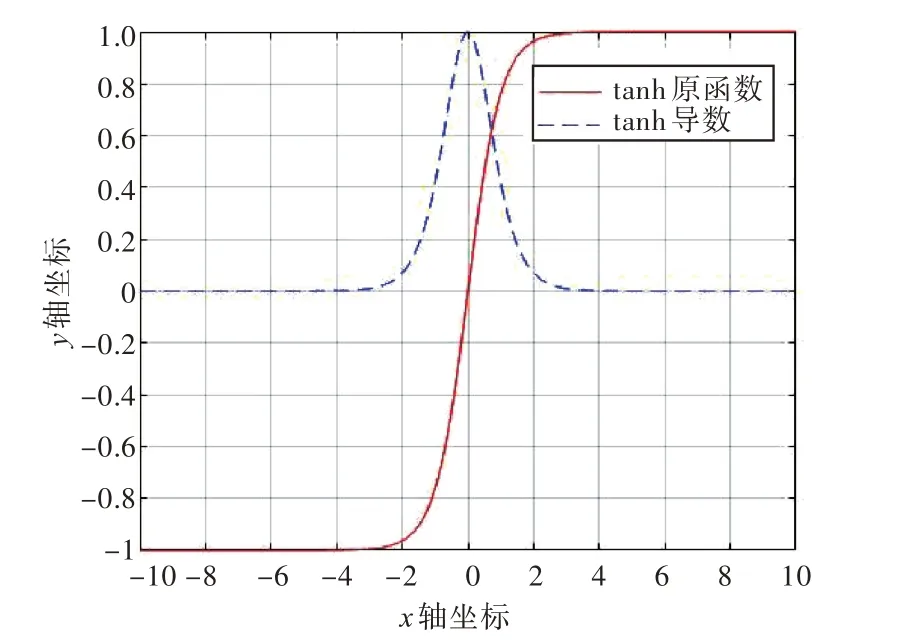
图4 双曲正切函数图像Fig.4 Graph of hyperbolic tangent function
式(7)表明,当父节点Pp延伸方向位于锥形碰撞区以内时,USV 航向偏危险,此时在原始延伸基础上,添加Po到Pp连线方向根据ω动态调节的R,让搜索树朝着远离障碍物的趋势延伸。图5所示为R与ω作用示意图。

图5 R 与ω 作用示意图Fig.5 Schematic diagram of the action between R and ω
由图4 可知,函数y=tanh(x)位于x轴正半轴部分有如下特性:1)当输入x∈(0,2)时,y∈[0 ,1]且数值变化剧烈;2)当输入x∈( 2,+∞ )时,y对x的变化不敏感。当 |PpPo|>Ls时,随着 |PpPo|的增大,根据特性2),此时ω值保持在1 附近,表现在USV 避障上则是当父节点Pp距离障碍物中心满足一定安全限度时,R的作用不明显;当|PpPo|<Ls时,随着 |PpPo|的减小,根据特性1),此时ω值将显著增大,表现在USV 避障上则是父节点Pp越靠近障碍物中心,R的作用越明显,使USV 航向向着远离障碍物的趋势延伸。
3.2 并行伸展与目标点吸引向量A 的设计
Bi-RRT 算法对两棵搜索树的父节点的定位与伸展规定了先后顺序,Ta产生新节点Pn后,Tb才能实施延伸步骤。尽管两棵树延伸有相互接近的趋势,但是这种顺序结构的执行无谓地消耗了运行时间。
为此,本文提出一种两棵搜索树并行伸展且在特定条件下具有相互接近趋势的改进方法。该改进方法通过两棵搜索树各自产生随机点,根据随机点各自选取父节点自行延伸的方式完成搜索树的扩展。R在特定条件下激发目标点吸引向量A,使搜索树并行拓展延伸的同时也不失Bi-RRT算法两搜索树相互趋近的优点。
在迭代过程中,设某棵搜索树基于式(1)得到Pn后,若α1>θ1,此时将触发本文改进Bi-RRT 算法中的A,在A作用下,延伸子节点Pn及其坐标不再满足式(1)和式(2),由过渡向量U及式(19)给出Pn'':

式中,Pg为目标点坐标。对于搜索树Ta而言,Pg为原始航线上航迹恢复点Xgoal;对于搜索树Tb而言,Pg为USV 当前位置Xinit。
式(9)表明,当父节点延伸方向位于锥形碰撞区外时,USV 航向偏安全,此时在原始延伸基础上,添加Pp到Pg连线方向上的A,使搜索树有朝着目标点生长的趋势。图6 所示为A作用示意图。

图6 A 作用示意图Fig.6 Schematic diagram of the action of A
3.3 改进Bi-RRT 自动避碰算法流程
由于本文两搜索树为同时并行延伸,互不干扰,因此以Ta为例,给出利用本文算法实现自动避碰的流程,如图7 所示。Tb除在第1 步初始化步骤中是以原始航线上航迹恢复点Xgoal初始化外,其他流程与Ta完全相同。
4 仿真结果与分析
为了验证改进Bi-RRT 算法的有效性,使用Microsoft Visual Studio 2017 开发环境编写C++程序进行仿真实验,并将Bi-RRT 算法与本文改进Bi-RRT 算法进行了对比。本文选取文献[14]所述高速USV 进行仿真实验,其航速为20 kn,设定单步探索步长S=10。
仿真实验中,USV 预定航线OS 设为二维坐标系第1 象限角平分线上从点(0,0)至点(100,100)线段;USV 当前位置Xinit设为(40,40);航迹恢复点Xgoal为(65,65);OS 上障碍物B1考虑安全区半径设为10,OS 周边障碍物B2,B3半径分别设为10,15;为了测试算法对各种避碰环境的通用性,B1,B2,B3圆心坐标O1,O2,O3均由C++程序随机数函数生成,作为算法输入,且限定O1在OS 上并位于Xinit与Xgoal之间;O2和O3距离OS 不超过25。

图7 改进Bi-RRT 自动避碰算法搜索树Ta 扩展流程Fig.7 The extension procedure of search tree Ta in improved Bi-RRT algorithm
图8 所示为Bi-RRT 算法与改进Bi-RRT 算法对随机障碍物避碰路径点生成情况对比。由图可见,USV 按照改进Bi-RRT 算法规划出的避碰路径点航行至航迹恢复点Xgoal的路径转向点明显减少,路径更加平滑。这是由于父节点延伸方向位于锥形碰撞区以外时触发了目标点吸引向量A,使两棵搜索树延伸更具有目的性,减少了因算法的随机性所带来的路径震荡问题。
由于两种算法均为随机算法,为了降低结果的随机性,提高论证的可信度,以该避碰环境作为输入,多次运行此两种算法,以比较路径点数目、父节点延伸失败次数与算法完成避碰路径点规划所消耗的时间,结果如表1 所示。图9所示为两种算法的搜索树延伸失败节点对比。
由于两种算法探索步长设置相同,因此路径点数目可以直接反映路径长度。由表1 与图8 可见,USV 按照改进Bi-RRT 算法规划出的避碰路径点航行至航迹恢复点Xgoal的路径长度明显短于同等条件下Bi-RRT 算法的结果。当航速一定时,使用改进Bi-RRT 算法规划出的路径不仅能使USV 能在更短时间内完成避碰动作,而且USV 所消耗的燃料也更少,对于提升USV 执行任务时的续航力有着重要意义。

图8 Bi-RRT 算法改进前、后避碰路径点规划对比Fig.8 The comparison of path point planning for automatic collision between basic and improved Bi-RRT algorithm
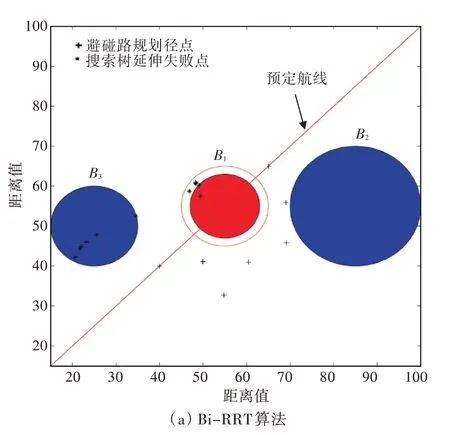

图9 Bi-RRT 算法改进前、后碰撞次数对比Fig.9 The comparison of collision times between basic and improved Bi-RRT algorithm
如表1 和图9 所示,改进Bi-RRT 算法两搜索树Ta与Tb父节点延伸失败次数明显少于Bi-RRT算法,改进Bi-RRT 算法搜索树延伸失败点数量明显少于改进前算法,这表明改进Bi-RRT 算法迭代过程中子延伸节点有更大概率通过“碰撞检测”,这是由于障碍物排斥向量R 与碰撞危险度系数ω动态调节父节点延伸方向,使延伸得到的新子节点能有更大概率得以保留,一定程度上加速了算法的收敛。由表1 对比,还可以发现,本文提出的改进Bi-RRT 算法在完成相同避碰路径规划任务时的耗时比改进前的算法有显著降低,这是由于两棵搜索树并行延伸扩展的方式以及当父节点延伸方向位于锥形碰撞区外时触发了目标吸引向量A,提高了算法的实时性。

表1 改进前后算法多次运行结果比较Table 1 The comparison of running result between basic and improved Bi-RRT algorithm
5 结 语
本文将Bi-RRT 算法与速度障碍法结合,针对父节点延伸方向位于锥形碰撞区内的情况,提出了障碍物排斥向量R与避碰危险度系数ω来动态调节父节点延伸方向,从而使搜索树向着远离障碍物的趋势延伸,并使延伸得到的新子节点能有更大的概率得以保留,从而加速算法的收敛。此外,提出了两棵搜索树并行延伸的方法,当父节点延伸方向位于锥形碰撞区外时触发目标吸引向量A,使两棵搜索树延伸更具有目的性,减少了由于算法的随机性带来的路径震荡问题。该改进算法未来可应用于对实时性要求更高的USV 动态避障问题,以及持续大风浪流扰动情况下USV 回归原预定航线的航迹滚动规划问题。

