水空跨介质航行器斜出水过程数值仿真

谭骏怡，胡俊华，陈国明，杨健，葛阳

空军工程大学航空工程学院，陕西西安710038

0 引 言

水空跨介质航行器（Trans-Media Aerial Underwater Vehicle，TMAUV）是指能够自主、反复跨越水空界面，并在空中和水中稳定飞行及航行的新型航行器［1-2］。一般多采用变体技术来完成空中和水下构型的转换，从而实现水空跨越。在军用领域，该类航行器可作为侦查平台来对抗信息感知能力，或作为攻击运载平台来提升武器突防能力，完成攻击任务；在民用方面，可作为远海探测器，通过在空中飞行快速接近目标区域后入水探测，探测完毕后再出水返航。其出水阶段全任务周期如图1 所示。

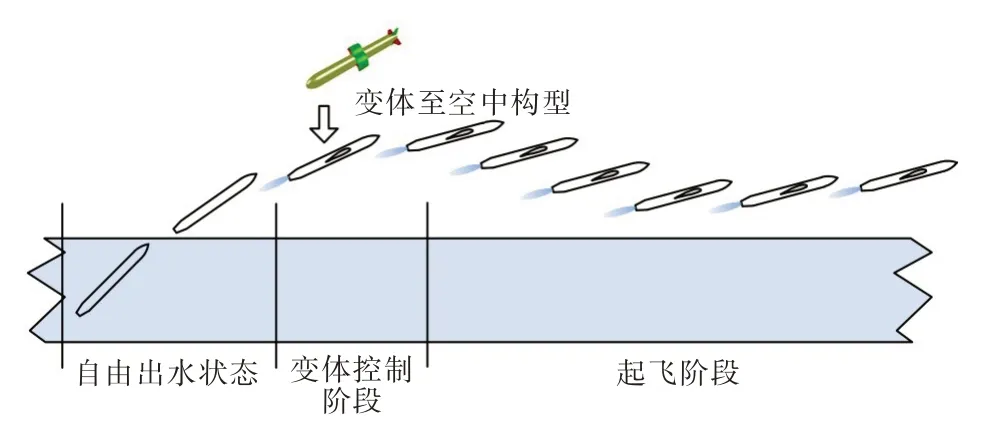
图1 水空跨介质航行器出水起飞过程示意图Fig.1 Schematic diagram of TMAUV in take-off and water-exit process

但不管是作为通信媒介还是水下发射的兵器，该航行器都要面临跨越水空界面的难题。航行器出水是一个十分复杂的过程，涉及固、液、气三相耦合等一系列复杂的物理问题。在出水过程中，液面会产生隆起变形，形成水冢现象，随后破裂并伴随有空泡的产生、溃散和液滴的分离飞溅［3］。这些强非线性、非定常现象会使航行器周围流场发生剧烈变化，其表面压力梯度会产生突变，因而对航行器跨越出水的稳定控制以及出水后的变体飞行提出了较高要求。因此，有必要研究水空跨介质航行器在不同工况下出水的流场特性以及航行器表面载荷的变化规律。

航行器出水的问题无论是在军事方面还是工程方面，都具有十分重要的意义。目前，对航行器出水过程特性的研究一般都集中在对简单物体（圆柱、球等）出水的流场特性分析和空化效应等方面。廖剑晖等［4］利用时变附加质量理论以及有限元思想，模拟了水下航行器的出水过程。姚熊亮等［5］通过改进二阶双渐进线法，分析了细长尖头圆柱体出水时的非稳态流场特性。孙士丽等［6］考虑了基于自由面效应的圆柱体出水运动数学模型并分析了水冢现象。李体方等［7］考虑了航行器在水下航行时波浪传播方向及相位对水下弹道的影响。胡俊辉［8］利用仿真软件模拟了航行器带空泡出水全过程，并对超空泡的形成过程及其与自由面的相互作用进行了研究。王一伟等［9］利用数值模拟的方法对结构体有攻角出水过程进行了研究。邹星［10］对结构体的出水过程流场和空泡演化规律进行了研究。彭立兵［11］采用模拟与实验相结合的方法研究了细长体出水过程规律，并分析了航行器头部形状与空泡产生规律的关系。以上大部分文献都主要集中于对简单结构体垂直出水相关特性的研究，尚未有针对特定鱼雷体构型在不同俯仰角和攻角条件下倾斜出水过程的数值仿真研究。本文将研究在不同条件下，特定构型斜出水过程的流场变化特性及机体载荷分布规律，从而为跨介质航行器实现稳定、反复跨越水空界面提供理论支持。

由于出水问题十分复杂，所涉及到的物理模型存在多相耦合、强间断、难收敛的问题，故目前还难以构建精确的数学模型。同时，开展实物出水试验对场地和设备要求较高，且对海浪、出水速度、出水角度等实验条件的控制难度大，成本较高。随着计算机技术的日趋成熟，利用CFD 流体仿真软件对出水过程进行数值模拟具有成本低、准备周期短、工况条件易于控制、重复性好、可信度高等特点，得到了各界的广泛使用。

本文将利用CFD 流体仿真软件，对水空跨介质航行器二维水下构型的斜出水过程进行数值仿真，研究航行器在典型工况下出水的气、液两相分布变化过程，比较出水过程典型位置的瞬时压力分布云图、速度云图及矢量场，分析航行器斜出水过程流场的变化规律以及航行器载荷的特性。通过对航行器在不同俯仰角及不同攻角下出水的数值模拟，分析水空跨介质航行器在斜出水过程中，俯仰角及攻角大小对周围流场及航行器载荷的影响，从而为研究水空跨介质航行器出水控制规律、制定最优的出水方案等提供理论支撑。

1 几何构型及仿真条件

1.1 几何构型及外形参数

水空跨介质航行器的三维几何构型如图2 所示。本文对水下构型进行了适当简化，省略了舵面并且未考虑机翼收回后表面的突起，简化后的航行器二维水下构型模型简图以及对俯仰角和攻角的定义如图3 所示。其中，航行器惯性主轴与水平面的夹角为俯仰角θ，速度矢量与惯性主轴的夹角为攻角α，速度矢量位于惯性主轴下方时为正，位于上方时为负。

图2 水空跨介质航行器三维几何构型Fig.2 Three-dimensional geometric model of TMAUV

图3 水空跨介质航行器外形参数及二维模型Fig.3 Geometric parameters and two-dimensional model of TMAUV

1.2 控制方程

流体控制方程主要包括连续方程、动量方程等，其通用形式［12］为

1.3 仿真方法可靠性证明

使用文献［13］构建的鱼雷出水动力学模型，在Matlab 软件中进行仿真计算，设定仿真初始条件为：初始出水角θ=45° ，初始速度v=10 m/s ，攻角α=0°，并将理论计算结果与流体仿真结果进行比较，得到出水位置姿态变化、位移变化、俯仰角度变化的规律如下。

1）出水位置姿态变化。

图4 所示为对理论模型进行仿真计算后，得到的航行器出水位置姿态变化轨迹对比曲线。

图4 水空跨介质航行器出水动力学模型位置姿态仿真Fig.4 Position and attitude simulation of dynamic model of TMAUV in water-exit process

定义航行器机体直径为D，机体顶点在惯性主轴方向上距离水面的长度为l，并且在水面上方为正，定义无量纲参数d=l/D。在相同工况下，对航行器出水过程进行CFD 流体仿真，对比航行器的姿态，如图5 所示。图5 中，左侧图为根据文献［13］所提水动力学模型计算得到的航行器相对于水面的位置，右侧为采用本文CFD 数值仿真方法得到的航行器位置。由图可知，采用本文数值仿真方法得到的结果与采用理论模型求解方法得到的结果基本一致。

2）位移变化。

图6 所示为航行器分别使用理论计算和流体仿真2 种计算方法得到的不同方向位移的变化趋势。从2 种位移变化来看，在一定时间内，其变化的趋势和规律基本一致。

图5 出水位置姿态的理论计算与流体仿真结果对比Fig.5 Results comparisons of theoretical calculation and fluid simulation of position and attitude in water-exit process

3）俯仰角度变化。

图7 所示为采用理论计算和流体仿真2 种方法计算得到的航行器俯仰角对比曲线。由图可见，采用流体仿真方法计算得到的航行器离开水面时俯仰角度为23°，采用理论模型计算得到的俯仰角度为21°，2 种方法的计算结果基本吻合。

图6 位移变化曲线Fig.6 Displacement curves

图7 俯仰角度变化曲线Fig.7 Variation curves of pitch angle

通过对理论计算和流体仿真2 种方法计算结果的对比，证明本文所采用流体仿真方法具有可靠性。

1.4 计算域及仿真条件

本文采用FLUENT 流体仿真软件进行数值模拟。使用ICEM CFD 软件绘制计算域网格，并对计算域中的自由面和航行器周围网格进行加密，网格数约8 万，计算域范围为50 m×40 m，水域和空气域高度各20 m，机体头部顶端距离水面1 m，如图8 所示。仿真过程采用有限体积法的多相流模型，湍流模型采用k-ε模型，将计算域上方边界设置为压力出口边界条件，航行器及计算域其他边界设置为固壁边界条件，在瞬态计算过程中采用SIMPLEC 算法求解控制方程，动量、湍动能及其耗散率均采用二阶迎风离散格式，压力插值采用PRESTO！离散格式。动网格更新方法采用弹簧近似广顺算法和局部重构算法，通过C 语言，编写用户自定义函数（UDF）对航行器出水速度进行定义，最终实现航行器的出水。

图8 出水过程计算域示意图Fig.8 Computational domain diagram of water-exit process

根据文献［14］，当该构型的出水速度达到20 m/s 时，只在尾翼处背水面产生了少量空泡，由于本文仿真采用的速度为10 m/s，且不考虑尾翼的影响，故不考虑流体的空化。同时，由于出水速度较小，所以在UDF 对流体的设置中认为流体是不可压缩的。

1.5 计算结果收敛性验证

图9 所示为出水过程仿真的残差收敛曲线。残差值指当次计算结果与上一次计算结果的差值，一般规定当残差值小于10-3时，说明计算结果达到稳定。从曲线收敛情况来看，出水过程仿真计算结果残差值在迭代至3 500 步以后，基本趋于稳定，且数值小于10-3，表明计算结果收敛了。

图9 计算结果残差收敛曲线Fig.9 Residual convergence curves of calculated result

2 水空跨介质航行器斜出水过程流场及载荷分析

2.1 气、液两相分布

图10 所 示 为 当α=0°，θ=45° ，v=10 m/s时，航行器斜出水时的气、液两相分布图。总共选取了8 个不同时刻，其中蓝色为水介质，红色为空气介质。出水过程大致可分为3 个部分［15］：液面变形（t2，t3时刻）、液面包裹出水（t4，t5，t6，t7时刻）及尾流断裂（t8时刻）。由图10 可看出，航行器在斜出水接近水面的过程中，水面会逐渐发生隆起变形，头部周围液体由于惯性和粘性作用具有一定的速度，并附着在航行器表面形成一层薄薄的液膜包裹着航行器。随着航行器的定速出水，两侧附着液体的压力减小，粘性力逐渐小于水的重力，致使航行器上的液膜破裂并顺着壁面滑落飞溅，从而使壁面暴露在空气中。随着航行器继续上升，液体滑落至尾部形成尾流，之后，尾流逐渐变细，中间部分内凹并发生断裂，完成出水。

图10 出水过程气、液两相分布Fig.10 Gas-liquid two-phase distribution of water-exit process

2.2 速度流场变化规律

为研究航行器在出水过程中周围液体的速度变化趋势和流场变化规律，在3.1 节的仿真条件下，选取了出水过程中12 个瞬时时刻，得到航行器周围流场的速度分布云图及流线图，如图11 所示（其中左图为速度云图，右图为流线图）。

由图11 所示速度云图的变化来看，当航行器在水下以10 m/s 的速度作直线运动时，周围液体由于壁面粘性的带动产生初始速度而随航行器一起运动，最大速度出现在底部中心红色区域，速度约为9 m/s，机身两侧速度相对较小，头部附近液体速度居于二者之间，约为4 m/s。随着航行器逐步跨越水面出水，尾部后侧液体尾流逐渐拉长，机身上半部附近的液体速度逐渐增大，变化趋势为向中部延伸。在头部跨越水面的瞬间，头部液体速度突然增大，出水后恢复正常，这是由于头部液膜结构破裂导致液体粘性阻力瞬间减小，在机体头部的推动下，速度出现了局部突变。头部出水后，机身两侧流场因受附着的水介质和空气介质的影响，液体速度分布变化剧烈，速度场产生震荡，在航行器完全出水后，液体速度场恢复稳定。

图11 出水过程流场速度云图及流线图分布Fig.11 Velocity contours and streamlines of flow field in water-exit process

从图11 所示流线图的变化来看，当航行器在近水面航行时，由于头部对液体的排挤作用，机身附近液体速度矢量呈放射状，并在机体两侧形成了较大的回流区；当头部接近液面时，在机体与头部连接处附近产生了漩涡，上侧漩涡方向以逆时针为主，下侧漩涡方向以顺时针方向。在头部出水的瞬间，此时航行器最高点已高于远场未扰动自由面，液面包裹头部，航行器即将进入空气介质，由于水、空介质的物理性质差异巨大，速度分布呈非对称性，而气、液两侧速度场分布的巨大差异也使得在界面上存在速度间断。此时，机身上侧漩涡的轴向和径向半径迅速增大，下侧漩涡的轴向半径迅速增大。头部出水后，其附近稳定的回流区被破坏，机身下侧漩涡最先发生分离，形成多个大小、强度不一的涡流，随后，机身上部漩涡也发生分离，出现了驻涡，从而使得航行器周围流场发生剧烈变化。当航行器完全出水后，机身两侧回流区逐渐恢复稳定。

2.3 流体作用力分布

水空跨介质航行器以恒定速度作倾斜出水运动时，周围流场受介质突变的影响会发生剧烈变化，而流场的变化会引起航行器壁面压力变化，影响其运动状态和出水过程中的稳定控制，严重时，还会导致细长体的损坏和折断。利用压力监视器可对机身表面所受的流体作用力进行监测，共监测得到110 组数据。将所有的点在坐标轴上进行标注并拟合成曲线，取航行器的惯性主轴为横轴，方向指向头部为正，表示机身表面位置，纵轴在纵向对称面内垂直于x 轴方向，表示流体作用力，方向指向斜上方为正。

图12 选取了与2.2 节相同的12 个瞬时时刻的压力云图和壁面所受流体作用力曲线，来研究航行器壁面的受力规律。其中左图为压力云图，右图为对应的航行器壁面受力曲线。

图12 出水过程流场压力云图及流体作用力曲线Fig.12 Pressure contours and hydrodynamic force curves of flow field in water-exit process

从总体的变化趋势来看，在航行器出水过程中，其尾部中段始终存在高压区，在尾部与机身连接处出现了压力极小值，其值随出水位置的不同大小也不同。当航行器在水下航行时，由于水的静压作用，机身上、下表面所选取的点所处水深不同，其表面存在压力差：上表面位置较浅，压力较小，下表面位置较深，压力较大。当航行器跨越水空界面时，由于介质突变、液膜的产生和破裂、液滴的分离飞溅等原因，机身上、下表面受力产生了不同幅度的震荡，局部出现了上表面压力大于下表面压力的现象。航行器完成出水的部分因受到空气介质的压力，上、下表面的压力差值恢复稳定，上表面压力大于下表面压力。

当航行器在水下航行时（t1=0.16 s），尾部上表面压力小于下表面压力，峰值差较小，机身上、下表面保持稳定的压力差。当航行器逐渐接近水空界面时（t2=0.28 s），尾部压力峰值差逐渐增大，机身上、下表面压力差值减小，并出现了正负交替现象。在头部出水过程中（t3=0.36 s，t4=0.44 s），此时头部已超过远场未扰动水面，处于液膜包裹、破碎瞬间，尾部压力峰值差持续增大，机身出现上表面压力大于下表面压力的情况，机身压力差变化剧烈，在机身与头部连接处出现压力极小值，下表面出现负压，产生俯仰力矩，头部顶端由于上侧液面比下侧液面上升的多，表现为压力降有所缓和。在机身出水过程中（t5=0.50 s，t6=0.54 s，t7=0.60 s，t8=0.66 s，t9=0.70 s），尾部压力峰值差始终较大，机身段由于有液体的附着干扰，压力差值出现了不同幅度的正负交替，出水部分的空中流场已得到稳定发展。当尾部高于远场未扰动面时（t10=0.76 s，t11=0.80 s，t12=0.90 s），由于液体尾流对尾部的附着作用，尾部上、下表面压力产生震荡并出现了2 个波峰，随后压力峰值差逐渐减小，在航行器完全出水后，受力恢复稳定。

图13 所示为航行器在出水过程中，在轴向和径向所受流体作用力的时间历程。从图中可以看出，航行器在水中航行时的受力呈现出了震荡现象，径向受力波动幅度较大，数量级达105，轴向受力波动较小，数量级为104。航行器在穿越水空界面进入空气后，与流体接触的面积减小，浮力和流体阻力逐渐消失，但仍存在自由面、液体尾柱和波浪力的影响，轴向受力和径向受力振动的幅度减弱，二者的振动幅度均小于数量级104。完全出水后，受力趋于稳定。

综上所述，航行器在出水的过程中其壁面受力变化非常剧烈，不同阶段会出现不同程度的幅度和正负震荡，产生附加力矩，从而对航行器的稳定性及机体结构产生严重的负面影响。

3 俯仰角和攻角的影响

通过上述分析发现，航行器出水过程中流场及载荷变化最为剧烈的位置是在航行器穿越水空界面的瞬间，航行器几何中心与液体远场未扰动面重合时刻前、后处，故定义前者为“位置1”，后者为“位置2”。下面，将研究以不同俯仰角和攻角出水时，在位置1 和位置2 处的流场及航行器壁面载荷变化规律。同时，定义“完全出水时间T”为航行器从相同潜深以相同速度运动，从穿越水空界面直至尾部尾流断裂所用时间。

3.1 俯仰角的影响

3.1.1 气、液两相分布云图

图14 所示为航行器在相同速度和潜深以及不同俯仰角下出水的气、液两相分布云图。其完全出水时刻分别为T15°=1.64 s，T30°=1.18 s，T45°=0.98 s，T60°=0.86 s，这说明俯仰角越大，完全出水时间越短，航行器受水空界面的影响时长也就越短。由图14（a）可以看出，在航行器出水的瞬间，θ=15°时液面隆起程度最为明显，隆起范围也最大，水冢现象最突出。但随着俯仰角的增大，水冢现象减弱，液面变化逐渐减小。其原因是航行器俯仰角越小，其在水平面的投影面积越大，航行器上表面“托起”的液体也就越多。由图14（b）可以看出，当航行器出水至位置2 时，俯仰角越大，航行器上侧液面附着面积越小，下侧液面附着面积越大，其穿越液面所需时间便越短，航行器受液面包裹的时间也就越短。

图14 不同俯仰角出水气、液两相分布云图Fig.14 Gas-liquid two-phase distribution contours of water-exit process at different pitch angles

3.1.2 流场速度流线图

航行器在位置1 时的瞬时速度流线图如图15所示。从尾部流线来看，当θ=15°时，尾流出现了涡脱现象。随着俯仰角的增加，航行器尾流逐渐缩短，涡脱现象消失，机身两侧逐渐形成了稳定的漩涡。当俯仰角较小时，机身两侧形成了面积较大的漩涡，范围覆盖整个机身，但随着俯仰角的增加，两侧漩涡轴向面积逐渐减小，上侧漩涡径向面积也逐渐减小，当θ=60°时，漩涡面积最小，该时刻未出现漩涡发放现象。

图15 不同俯仰角出水流场速度流线图（位置1）Fig.15 Velocity streamlines of flow field in water-exit process at different pitch angles（position 1）

航行器在位置2 时的瞬时速度流线图如图16所示。由图可看出，当θ=15° 时，由于液体的附着，在机身两侧漩涡呈现稳定的两部分，上半部漩涡轴向长度短、径向宽度长，下半部漩涡轴向长度长、径向宽度短；但随着俯仰角的增大，机身上侧下半部的涡逐渐上移与上半部的涡合并，在θ=60°时形成了一个稳定的驻涡，范围覆盖整个机身上侧。而下侧的上、下半部漩涡则随着俯仰角的增加，逐渐向中间合并为一个涡。机身两侧存在的漩涡会在径向产生交变应力，对航行器的控制造成影响。

图16 不同俯仰角出水流场速度流线图（位置2）Fig.16 Velocity streamlines of flow field in water-exit process at different pitch angles（position 2）

3.1.3 航行器壁面载荷分布

图17 和图18 所示分别为航行器在位置1、位置2 的壁面所受的流体作用力曲线。

图17 不同俯仰角出水流体作用力曲线（位置1）Fig.17 Hydrodynamic force curves of vehicle in water-exit process at different pitch angles（position 1）

图18 不同俯仰角出水的流体作用力曲线（位置2）Fig.18 Hydrodynamic force curves of vehicle in water-exit process at different pitch angles（position 2）

在航行器出水的瞬间，不同俯仰角下航行器壁面的载荷分布规律相似，在尾部中段出现了高压区，沿横轴方向压力骤减，而在其与机身连接处则出现了低压区。当θ=15°时，尾部压力峰值差约为30 kN，但随着θ的增大，尾部压力峰值增大，当θ=60°时，峰值差为46 kN。机身上表面压力大于下表面压力，压力差变化明显。 当θ=15°时，机身上、下表面压力差相对稳定，约为10 kN，当θ增大至60°时，压力差平均值达20 kN 以上。在头部顶端附近出现了壁面受力最大值，当θ=15°时，压力最大值达90 kN，但随着θ的增大，压力最大值逐渐减小。

航行器出水至位置2 时，除尾部外，机身上表面压力小于下表面压力，θ越小，附着有液体的表面载荷变化越剧烈，范围更大。当θ=60°时，航行器暴露在空气介质中的面积最大，其空气中流场发展得最稳定。

从以上2 个典型位置、不同俯仰角航行器所受流体力曲线来看，本文的几何构型由于在尾部与机身连接处、机身与头部连接处存在几何折角，导致了该处的压力突变，因此在外形结构上还需要进一步优化。可以看出，出水过程中航行器的载荷特性十分复杂，变化非常剧烈，因而对航行器出水稳定控制和材料结构特性均有较高的要求。

3.2 攻角的影响

考虑到航行器在水下有大角度机动的情况，水下航行一般取攻角范围为-15°～15°［15］。本文选取攻角范围为-10°～10°来研究攻角的影响。

3.2.1 气、液两相分布云图

图19 所示为航行器在θ=45°，v=10 m/s，不同攻角下出水时，在2 个典型位置处得到的气、液两相分布云图。由图可见，当攻角为正时，机身上侧附近液面出现了凹陷，机身下表面附近液面由于航行器的挤压作用和流体粘性的作用而高于远场未扰动液面；随着攻角的增大，上侧液面凹陷及下侧液面隆起程度加剧，当攻角达到10°时，机身上侧液体已脱落至中段，而下侧附着液体还完全覆盖着头部。当攻角为负时，情况正好相反，机身上侧附着的液面高于下侧，上侧液面隆起及下侧液面凹陷的程度随着攻角的增大加剧了，当攻角为-10°时，机身下侧附着的液体已脱落至中下段，上侧液体滑落至头部与机身连接处。由此可见，与零攻角相比，带攻角出水的多相耦合更为复杂，两相流变化更为明显。

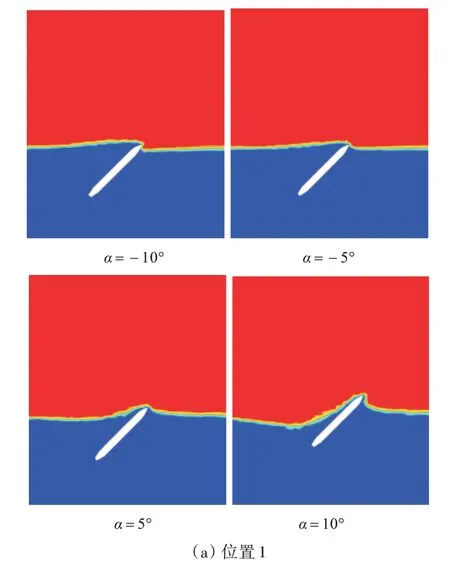
图19 不同攻角出水气、液两相分布云图Fig.19 Gas-liquid two-phase distribution contours of vehicle in water-exit process at different attack angles

3.2.2 流场速度流线图

图20 和图21 所示分别为航行器在θ=45°，v=10 m/s，不同攻角条件下出水时，在2 个典型位置处得到的流场速度流线图。

图20 不同攻角出水流场速度流线图（位置1）Fig.20 Velocity streamlines of flow field in water-exit process at different attack angles（position 1）

图21 不同攻角出水流场速度流线图（位置2）Fig.21 Velocity streamlines of flow field in water-exit process at different attack angles（position 2）

由图20 可看出，在航行器出水的瞬间，当攻角为负时，头部下侧流场产生了顺时针的漩涡，涡核位于头部与机身连接处，尾部左后侧流场产生了逆时针的漩涡。随着攻角的增大，头部下侧漩涡范围逐渐向涡核收缩，尾部左后侧漩涡出现分离并逐渐稳定在尾部与机身连接处，形成驻涡。当攻角为正时，在头部上侧周围流场以及尾部周围、尾部与机身连接处均产生了漩涡，与攻角为负时的情况正好相反。随着攻角的增大，头部附近漩涡逐渐收缩，尾部与机身连接处漩涡逐渐脱落，与尾部附近漩涡融合。

由图21 可看出，航行器在跨越水面的过程中，在头部下侧及尾部后侧均形成了漩涡，漩涡对流场速度场的扰动范围比位置1 处的大；当攻角增大至-5°时，尾部与机身连接处产生了漩涡，并与尾部后侧相互扰动。当攻角为5°时，在头部上侧、机身与尾部连接处产生了漩涡，与攻角为负时正好相反。当攻角增加至10°时，尾部漩涡脱落，在尾部后侧流场形成周期性的漩涡发放。

由此可以看出，与零攻角相比，在带攻角出水瞬间，头部和尾部两侧会形成方向相反的漩涡，从而产生巨大的俯仰力矩；随着攻角的增大，涡流逐渐从尾部脱落，速度场变化反而小于小攻角状态。

3.2.3 航行器载荷分布

图22 所示为航行器以不同攻角出水至位置1处时表面所受流体作用力曲线。与相同条件下的零攻角出水结果相比，当α=-10°时，机身上、下表面平均压差值较大，并且在其下表面出现了幅度明显的压力值震荡；压差最大值明显增大，但头部顶端压力有所下降。当α=-5°时，尾部及机身下半部受力较大，头部压力值及上、下表面压差较小，且在前半部出现了压差值正负反向。当攻角为正时，载荷分布与零攻角时的状态相似，压差值无显著变化，但航行器正攻角出水相当于在其径向增加了一个速度矢量，从而使得航行器下侧对液体有挤压作用，流体作用力较大，导致机身上表面压力小于下表面压力。

图22 不同攻角出水的流体作用力曲线（位置1）Fig.22 Hydrodynamic force curves of vehicle in water-exit process at different attack angles（position 1）

图23 所示为航行器以不同攻角出水至位置2处时表面所受流体作用力曲线。与相同条件下的零攻角出水结果相比，由于带攻角出水上、下两侧附着液体的高度和相位差异较大，导致机身表面受到的流体作用力出现大幅震荡，压力差值不断变化，尾部峰值差变大，从而产生瞬时变化的附加力矩，影响航行器成功出水。

图23 不同攻角出水的流体作用力曲线（位置2）Fig.23 Hydrodynamic force curves of vehicle in water-exit process at different attack angles（position 2）

4 结 论

本文基于CFD 流体仿真技术，采用编制用户自定义函数控制航行器运动，分析了航行器在典型工况下的斜出水过程，通过仿真对比，分析了航行器斜出水过程中的流场变化规律和航行器载荷特性，阐述了在不同俯仰角、攻角条件出水对流场及航行器载荷的影响规律，得到以下主要结论：

1）航行器在倾斜跨越水空界面时，会依次出现液面变形隆起、液面附着包裹出水以及尾流的拉曳断裂现象，从而导致航行器周围流场发生突变和持续的剧烈变化，在两侧形成半径、方向不一的回流区，航行器被水包裹部分机体载荷出现高频率的正负交替震荡，产生俯仰力矩。

2）在航行器出水的瞬间，俯仰角越大，航行器受水空界面的影响时长越短，水冢现象和涡脱现象减弱，流场漩涡径向半径减小，速度流场受扰动范围减小。在出水过程中，俯仰角越大，受驻涡影响，越容易产生交变应力，影响航行稳定。

3）与相同条件下的零攻角出水结果相比，在航行器带攻角出水瞬间，上、下两侧附着液体的高度和相位差异较大，同时在头部和尾部两侧形成反向漩涡，机身表面受流体作用力出现大幅度的震荡。随着攻角的增大，涡流会逐渐从尾部脱落，压力差值会不断变化，尾部峰值差变大，从而产生瞬时变化的附加力矩，影响航行器成功出水。