基于SARIMA 模型的舟山制造业PMI预测能力分析

□刘嘉诚

采购经理指数（Purchasing Managers' Index，简称PMI）是通过对企业采购经理的月度调查汇总出来的指数，因其具有及时性、先导性、综合性和指导性等特点，使得该指数在经济预测和商业分析等方面都有着重要的意义。PMI 具有较强的实际应用性，本文以舟山制造业月度PMI 数据为基础，通过建立SARIMA 模型对舟山制造业PMI 的预测能力进行评价。

数据来源及预处理

本文选取2015 年3 月至2019年4 月舟山制造业月度PMI 共50 组数据，其中使用2015 年3 月至2018年10 月的44 组数据进行建模，用2018 年11 月 至2019 年4 月 的6 组数据进行模型检验。此外，为了减少异方差的影响，对这组序列进行自然对数转换，其中pmi 表示舟山制造业月度PMI 序列，lpmi 表示进行对数转换后的序列，dlpmi 表示进行一阶逐期差分平衡后的序列，sdlpmi 表示进行一阶逐期差分和季节差分之后的序列。

模型的建立

SARIMA 模型的建立主要包括四个步骤：平衡性检验、模型的定阶与识别、模型的参数估计、模型的诊断与检验。

（一）平衡性检验。

在对一个时间序列进行建模前，首先应当考察该序列的平稳性。如果序列是不平稳的，则需要对序列进行差分，使得差分后的序列成为平稳时间序列。本文对序列的平稳性检验采用最为常用的ADF 单位根检验方法。

从图1 单位根检验结果可以看到，原始序列lpmi 是非平稳序列，在进行一阶逐期差分处理后的序列dlpmi 是平稳序列，因此dlpmi是一阶单整序列，可以得到d=1。进行一阶逐期差分和季节差分处理后的序列sdlpmi 是平稳序列。同时该序列已消除了原时间序列lpmi的季节性，因此D=1。从dlpmi 的自相关和偏相关图分析，序列在k=12时显著不为零，可以得出序列存在以12 个月为周期的季节波动，经过上述检验和处理，原始序列lpmi 满足建模要求，可以以序列sdlpmi 为基础建立SARIMA 模型。

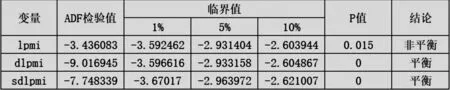
图1 ADF 单位根检验结果

（二）模型的定阶与识别。

由于上文确定原始序列lpmi的非季节差分阶数d=1；季节差分阶数D=1，故考虑建立SARIMA(p，d，q) (P，D，Q)12 模型进行分析与预测，接下来确定p、q、P、Q 的取值。

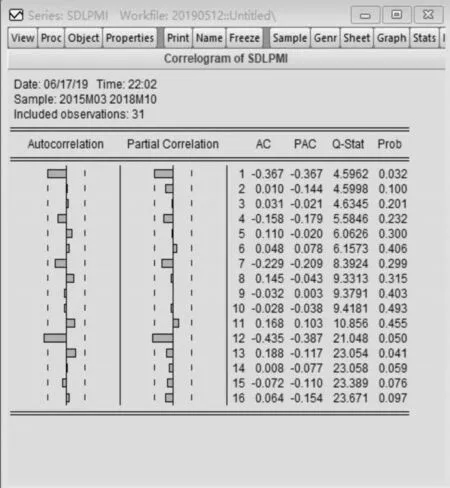
图2 sdlpmi 序列的自相关和偏相关图

观察分析序列sdlpmi 的相关图和偏相关图（如图2），如果把自相关函数看作截尾特征（K＞13 后截尾），把偏自相关函数看作是拖尾特征，应该有一个乘积季节移动平均模型，推出q、Q 可以等于1，考虑建立(0，1，1)(0，1，1)12。如果把自相关函数看作拖尾特征，把偏自相关函数看作截尾特征（K＞13 后截尾），应该加入一个乘积月度自回归模型，推出p、P 可以等于1，考虑建立(1，1，0)(1，1，0)12。

通过观察序列的自相关和偏相关图，结合上述的判断，对可能性最大的六个模型进行比较测试评价，分别是(1，1，1)(1，1，1)12、(1，1，0)(1，1，1)12、(1，1，0)(1，1，0)12、(1，1，1)(1，1，0)12、(1，1，1)(0，1，1)12、(0，1，1)(0，1，1)12。

接下来依次对六个模型进行单位根检验，如果模型的单位根有个等于1，说明模型是不可逆的，过程是不平稳的。通过对六个模型单位根的判断可以得出，除(1，1，0)(1，1，1)12和(1，1，0)(1，1，0)12两个模型之外，其他四个模型中的单位根均存在等于1 的根。

接下来对这两个模型进一步评价。在选择模型时，一般根据AIC 值和SC 值最小的准则作出选择。(1，1，0)(1，1，1)12模 型：AIC=-3.21267，SC=-3. 027639；(1，1，0)(1，1，0)12模型：AIC=-3.238941，SC=-3.100168。因此，选择模型(1，1，0)(1，1，0)12较为合适，结果更理想。

（三）模型的参数估计。

建立模型(1，1，0)(1，1，0)12，用2015 年3 月至2018 年10 月的月度数据对模型进行参数估计，得到结果如下：

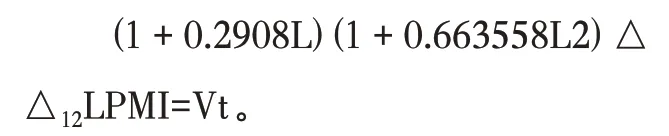
其中，R2=0.52，DW=2.13，Q(16)=9.68，χ20.05(15)=24.99

（四）模型的检验。

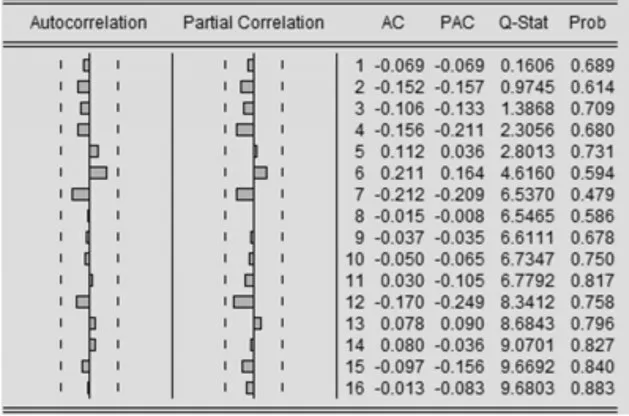
图3 残差序列的自相关和偏相关图

对模型估计结果进行检验，包括模型特征根值的检验、参数估计的t 检验和残差序列的Q 检验。

首先是特征根值的检验，该模型的特征根值都在单位圆之外，说明模型满足检验要求。其次参数估计的t 检验，残差序列的自相关系数均落入随机区间内，且P 值均较为显著，说明残差序列不再有自相关成分，且模型参数具有显著性，通过t 检验。最后是残差序列的Q 检验，以Q(16)为例，Q(16)=9.68＜χ20.05（15）=24.99，模型的误差项通过Q 检验。综上分析，可以确定最终建立的模型为(1，1，0)(1，1，0)12模型。

模型的预测能力评价

根据建立的模型，首先对样本内2017 年5 月-2018 年10 月 共18 个月的PMI 进行静态预测，通过实际值与预测值的比较来判断模型的预测精度，然后继续利用模型对样本 外2018 年11 月-2019 年4 月 共6个月的PMI 进行动态预测。

从衡量指标看，模型的拟合结果是较好的。首先分析评估静态预测结果，均方根误差(RMSE) 为2.1858、平均绝对误差(MAE) 为1.8026，两个数值均较小；平均相对百分比误差(MAPE)为3.77%，泰勒不等系数(TIC)为0.0227，其中泰勒不等系数(TIC)越小，拟合度越好；总体而言这些衡量指标说明该模型具有较好的拟合效果。

从实际值与预测值的误差率来看，预测效果是不理想的。首先看静态预测结果，如表1 所示，相对误差平均值为3.78%，误差率最高为9.09%，最低为0.2%。18 组静态预测结果中，只有两组的相对误差在1%以下，说明预测数据的相对误差率是较高的。再看动态预测结果，6 组动态预测结果中，只有1组的相对误差率在1% 以下，如2019 年2 月的相对误差率竟然达到13.59%。综上，从实际预测结果看，该模型的预测误差率较高，预测值与实际值存在较大差距，模型的预测结果是不理想的。

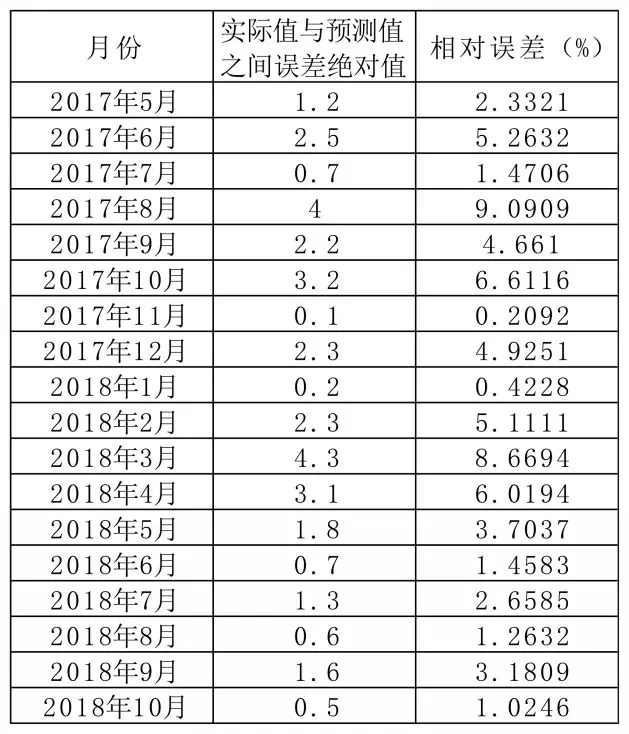
图4 静态预测结果

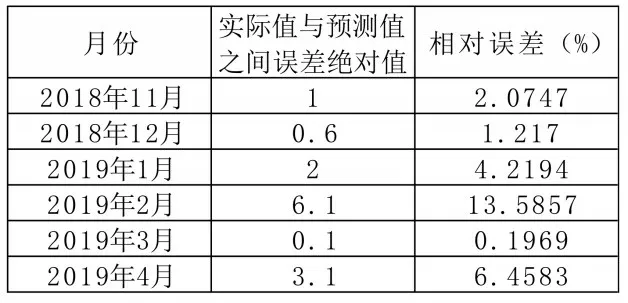
图5 动态预测结果

模型预测存在的缺陷及建议

（一）逐步扩充基础历史数据序列。如前文所述，尽管SARIMA方法可以为任何周期的经济时间序列建模，但需要足够多的基础数据（序列观测值）作为支撑。建立SARIMA 模型，对于季度序列最好在100 个以上，对于月度序列则应该更多。而本文基于月度序列建立的模型，其序列观测值个数只有44 个，在进行一阶逐期差分和季节差分之后，观测值更少。另一方面，月度PMI 基本在50 上下波动，月度波动的幅度非常非常小，有时只有0.1%或0.2%左右，这就需要模型具有非常好的拟合性和非常低的误差率。而分析本文中所建立的模型，尽管从几个衡量指标看具有拟合效果和一定的预测的作用，但是就实际误差率而言，预测效果是不理想的，是无法解释当前的时间序列。为此要逐步扩充基础历史数据（序列观测值），通过观测值来进一步识别合适的P、Q 等参数，建立较理想的SARIMA 模型，进一步提升数据支撑力度，增强模型的拟合效果。

（二）持续探索合适NBS 季调参数。除数据序列预测值不够多这个明显缺陷之外，月度PMI 数据匹配性协调性较差，也是导致模型预测效果不理想的原因。就季节调整本身而言，一方面，时间序列越长季节调整的效果越好，通常不能少于10 年，最好是一个经济周期的时间。舟山制度业PMI 调查从2012 年开始，月度PMI 的正式试算从2015 年开始，显然还没有经历一个完整周期，所以季节调整本身就不是很完善，存在很多缺陷。另一方面，目前月度PMI 数据都是通过NBS 数据处理软件，经过季节调整推算而来，NBS 季调软件中参数的设定，包括arima 模型、工作日效应、交易日效应以及节假日参数的设定等等，都会导致最后季调结果的不同。因此建议要不断研究NBS软件的运行原理，探索符合舟山实际经济发展状况的各项参数，确保季调后的PMI 数据不失真，更有匹配性、协调性。

结论

一方面，以舟山制造业月度PMI 数据为序列是可以建立合适的SARIMA 模型，而且建立的模型也具有一定的拟合效果和预测能力，同时也说明建立相应的模型对PMI自身进行短期或长期的预测具有较强的可行性。另一方面，受限于数据序列观测值很少，数据匹配性协调性较低等自身的缺陷，再加上PMI 序列具有很低的波动性等高要求，本文中模型的预测误差率还是偏高的，预测值与实际值存在较大幅度的差距，无论是静态预测还是动态预测，其预测结果是不理想的，预测能力也是有限的。综上所述，基于SARIMA 模型的舟山制造业PMI 预测能力目前来看是较低的，但是从长期来看具有较大的上升提高空间。如果能逐步扩充基数数据序列并不断提高数据匹配性协调性，SARIMA 模型的预测能力也会得到进一步的提高，预测效果得到进一步的增强。