对黄金价格的预测
杨震锐 王昊
【摘要】黄金作为一种具有金融属性的产品,其价格变化直接决定了黄金投资者和生产者的价值行为,同时,黄金价格的动态演变过程也是金融市场经济行为主体投资决策的反应。对黄金价格的预测有助于为黄金投资者与生产者的决策提供帮助。本文通过建立ARMA模型对黄金价格进行預测,结果反映,AR(1,6)形式的模型在预测黄金价格中表现较好。ARMA模型能在一定程度上预测黄金价格。
【关键词】ARMA 黄金价格 单位根
一、数据处理以及分析
黄金价格有着较为明显的时间趋势,黄金价格首先逐渐增加,会后有所回落。黄金价格整体是增加的。此外,我们应当对黄金价格的季节性进行弱化处理,黄金价格在理论上存在着季节性,尽管在统计数据上并非非常明显,但为排除季节因素可能造成的不利影响,需要对黄金价格取自然对数,通过这种处理来达到将价格数据p转变为更加平稳的1p(1p为p取自然对数)
取对数后,由于1p仍然具有比较明显的时间趋势,因此我们对1p进行一阶差分。进行一阶差分后,dlp没有明显时间趋势。为检验dlp的平稳性,我们进行DF检验。
从DF统计结果中我们可知,DF统计量结果为-16.318<-3.475(左边单侧检验),因此我们可以在1%的水平上拒绝原假设,即不存在单位根。由于DF检验中扰动项有可能存在自相关,因此我们还需进行更高阶的ADF检验。我们采用Schwert(1989)的方法,令最大滞后阶数为12*[(T/100)-(1/4)].其中,T为样本容量,并对最终结果取最大整数。使用从大到小的序贯规则,看ADF检验中最后一阶回归系数是否显著。计算可知,最大滞后阶数为14。
使用序贯规则,当滞后阶数等于10的时候,最后一阶滞后项(LIOD)在5%的水平上是显著的。我们可以看出,z(T)表明,可以在5%的水平上拒绝存在单位根的原假设。(-4.610<-3.478)由此,我们认为dlp为平稳序列。即对1p进行一阶差分后我们得到的时间序列是平稳的。
二、ARMA模型识别
从自相关以及偏相关图中,我们可以大致判断ACF以及PACF函数都存在着截尾的现象。并且第6阶自相关与偏相关系数较为显著(不为零)。从而这种情况下可以认为6阶以上的自相关与偏相关系数为0。由于白相关以及偏相关系数都存在着截尾的现象,我们分别考虑AR(6)以及MA(6)模型。
由Q检验结果中可知,AR(6)模型可以接受残差项无自相关的原假设。在AR(6)模拟结果表中,可知AR(6)模型中第1阶,第6阶较为显著。而2至5阶的系数并不显著。为此,考虑更为简洁的模型,将AR(6)模型中第2阶,3阶,4阶以及5阶变量省略,并进行重新估计。得到模型AR(1,6)
其次,估计MA(6)模型,由Q检验结果中可知,MA(6)模型可以接受残差项无自相关的原假设。在MA(6)模拟结果表中,可知MA(6)模型中第1阶,第6阶较为显著。而2至5阶的系数并不显著。为此,考虑更为简洁的模型,将MA(6)模型中第2阶,3阶,4阶以及5阶变量省略,并进行重新估计。得到模型MA(1,6),这与上文是一致的。
综上,我们建立了AR(6),AR(1,6)MA(6),MA(1,6)总共四个模型,为了选择更好的模型,我们使用AIC信息准则和BIC信息准则来选择更为合适的模型。
通过观察比较信息准则,在AIC信息中,AR(1,6)有着最小的AIC信息,在所有的BIC信息中,AR(1,6)同样有着最小的BIC信息。因此,我们最终选择AR(1,6)模型,并通过AR(1,6)模型进行预测。
从而,我们的模型为:
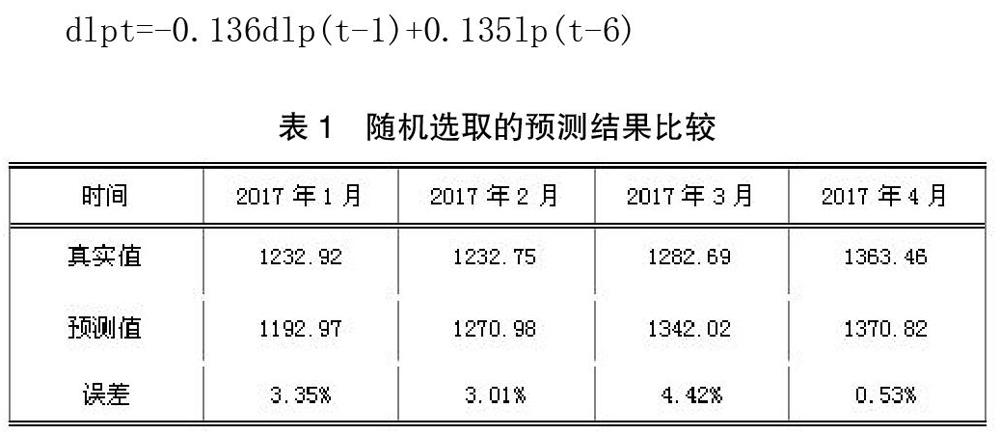
dlpt=0.136dlp(t-1)+0.1351p(t-6)
三、模型预测
由此可见,ARMA模型对黄金价格有一定的预测能力,但是由于黄金价格影响因素众多,ARMA模型仅仅基于黄金自身价格时间序列进行预测分析,从而并不能完全有效的对黄金价格进行预测。但是ARMA模型可以为黄金价格的变动提供一个基本的参照。

