黄金价格影响因素及时间序列分析
摘 要:黄金是重要的全球性投资工具。作为一种贵金属,它的保值功能在动荡时期尤为明显。自从布雷顿森林体系的建立将美元与黄金挂钩,其他货币与美元挂钩后,黄金的地位变得更加举足轻重。金价的波动往往会对美元价格、汇率和国家间的贸易平衡带来直接的影响,因此对金价影响因素的分析显得十分重要。首先,本文建立了一个关于可能影响金价的变量的多元线性模型并对其进行了修正。在第二部分中,我们主要分析了历史价格与黄金现价的关系及这种关系的具体表现形式。时间序列法在金价预测模型中应用很广,因为它能模拟历史数据的变化趋势并将发现的规律用于未来价值预测。通常,影响金价的因素有美元指数、通货膨胀、股票价格、利率政策、原油价格、黄金市场供求等。其中美元指数和油价通常是研究金价变动的关键变量。本文从理论角度解释了金价与美元指数、油价的关系,并通过建立模型,检验了市场中的真实数据是否符合理论预期。
关键词:黄金价格;美元指数;原油价格
一、价格影响因素模型
1.样本数据描述
选取从2013年1月至12月纽约黄金交易所的日收盘价(美元/每盎司),共259个标的。再选取同期的美元指数和原油价格(美元/每桶),也是各259个标的。构建方程预测12月22日到28日的金价。
2.影响因素
(1)美元价格变动
一方面,美元是国际黄金市场的报价货币,与金价呈负相关。另一方面,黄金又是美元资产的替代投资品。若美元有升值预期,人们将会追逐美元而使金价下跌。反之,美元越疲软,黄金越坚挺。在接下来的分析中,美元指数代表了美元价格的变动情况。
(2)原油价格
通货膨胀水平往往会给国际原油价格带来巨大影响。由于黄金具有防止通货膨胀的功能,因此金价与国际原油价格之间存在正相关。
(3)道琼斯指数(DJI)
DJI与金价的关系不是很明确。因为黄金具有商品属性,有时DJI下降(意味着商品价格下跌)会导致金价下降。有时DJI下降会迫使资本流入黄金市场进行套利,从而使金价上升。但有时DJI的上涨使人们认为美国经济向好,导致美元升值和金价贬值。
3.选择变量
根据以上影响因素,我们选出了以下相关变量:
4.选择经济学模型
建立如下回归方程:G=β0+β1O+β2U+β3DJI+E
为方程的常数项和各自变量的系数,E为残差,代表其他外部变量,例如供需变化、战争、金融危机等。
5.回归系数检验
(1)T检验
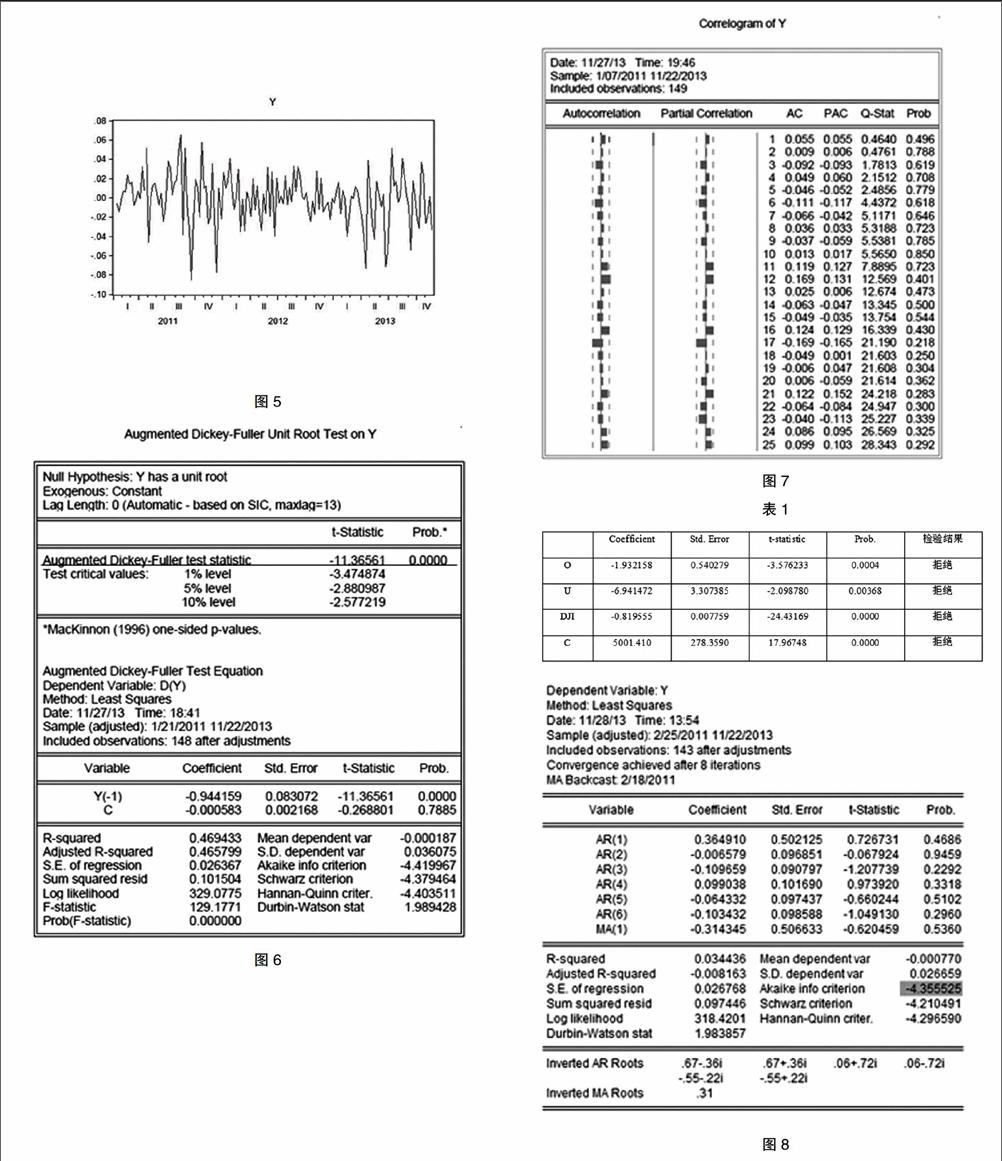
检验模型的最优线性无偏性(BLUE)将决定是否可以用OLS预测金价水平。T检验用于确定系数是否显著。假设置信水平为10%。原假设为:=0,备择假设为:≠0。根据下表的检验结果,常数和系数均显著。因此拒绝原假设,变量均可很好地解释因变量。
(2)拟合优度检验
使用来检验模型的拟合优度。越大说明数据对模型的拟合度越好。用EVIEWS获得如下结果:由于和均大于0.75,可知数据拟合度良好。
(3)残差检验
我们通过Jarque-Bera(JB)检验来测试残差(E)的正态性。在10%的置信水平下,H0:残差是正态分布;H1:残差是非正态分布。由下表知:E的JB值较低,因此拒绝原假设,残差是非正态分布的。
(4)相关性检验
实施Breusch-Godfrey序列相关性检验。置信水平为10%。H0:误差项没有自相关;H1:误差项有自相关。根据下表,因为g在拒绝区域内,所以拒绝原假设,即误差项存在自相关。
(5)异方差检测
使用怀特检验:首先使用OLS预测模型并得到残差,然后,运行辅助回归并得到TR2~X2(m)。若X2检验值大于对应值,则拒绝原假设。由下表知模型存在异方差。
(:误差是同方差的;:误差是异方差的。)
(6)模型的修正和改进
①自相关的修正
使用Corchrane-Orcutt法消除误差的自相关,结果如下:
②异方差的修正
使用异方差-一致性标准差来消除异方差,调整方程,结果如下:
(7)预测
经过了以上的检验和修正,我们得到了新的预测方程:
G=2406.654-0.060186O-16.28379U+0.012547DJI
由方程可知,油价与金价呈负相关,这与现实不一致。由于通胀率、利率等数据难以收集,我们无法对这些变量进行研究,这可能是误差产生的主要原因。为了使预测更加准确,我们将使用时间序列模型。
二、时间序列模型
为了更好地理解黄金价格,本文使用了多元时间序列模型来检验金价和它之前价格水平的相关性。由于黄金日价格波动幅度较大难以预测,我们从纽约商品期货交易所(COMEX)选取2011年1月7日到2013年11月22日的150个以周为统计频率的黄金收盘价格(closing price)作为观测对象(CLOCOMEXGOLD)。
1.稳定性和单位根检测
首先,需要检验数据的稳定性。使用EVIEWS5.0检测,结果如下:
图1
如图1,很明显纽约商品交易所的金价上下波动较大,没有明显的趋势可用于预测未来价格,数据不稳定。为了让数据更合理,需要进行单位根检验。
:CLOCOMEXGOLD有一个单位根:CLOCOMEXGOLD没有单位根。
图2
由图2知,在10%的显著水平下,由于P值为0.679>0.1,所以拒绝原假设,被测试数据CLOCOMEXGOLD没有单位根。
由以上检验结果可知,无论使用定性还是定量的检测方法,数据都是不稳定的。因此接下来需要将它们转化为稳定数据。在这之前,我们还需要将检测对象CLOCOMEXGOLD取对数。这么做的原因是对数形式更利于保持变量的稳定性并削弱异方差的影响。取对数后,我们就可以检验新数据的稳定性了。根据图3和图4,可以发现取对数后的数据依然是非稳定的。
图3
图4
实施自回归滑动平均模型(ARMA)的前提是确保数据的稳定性,所以必须考虑另一种方法:取一阶差分。输入命令‘genr y=d(logclocomexgold),新变量Y产生,它表示原数据对数的一阶差分。经过同样的检验后,Y数据趋于稳定了。由图5知,无论单个数据多么不稳定,它总是会归于一个均值。而且单位根检测也同样显示数据是稳定的(P=0小于置信水平10%)。
2.ARMA模型
得到稳定的数据集后,可以开始建立ARMA模型了。通过观察Y的相关图(图7),还无法明显地看出自回归模型(AR)和移动平均模型(MA)的阶数。因此,需要使用赤池信息准则(Akaike information criterion,AIC)和西沃兹信息准则(Schwarz information criterion,SIC),比较AIC和SIC的值,其中较小的一个可以决定ARMA模型的阶数。下表1是不同的AR和MA组合下的AIC结果,其中ARMA(5,1)为较小值。为了更加精确,继续深入检测ARMA(6,1)的AIC和SIC值,分别是—4.355525和—4.210491,比ARMA((5,1)的值小但所有系数都不显著,所以我们还是取ARMA (5,1)。图8显示了结果。
图5
图6
构造ARMA(5,1)模型,它描述了黄金现价与之前价格的关系。图9显示了每个系数的显著性。AR(2),AR(3),AR(4)和AR(5)的P值都超过了0.1,AR(1)和MA(1)的系数分别为0.988和0.946.
3.残差检验
本模型建立的假设前提为:干扰项为白噪声过程。因此建立模型后,需要进行诊断性检验,即残差检验。首先,从图10可看出,残差趋于回归它的均值,于是单位根检验可以拒绝原假设:残差有一个单位根,即残差不存在单位根,残差为白噪声,模型是有效的。
4.预测
时间序列模型的主函数是为了预测未来的黄金价格。如图12所示,通过进行静态预测,未来预测价格(YF)是在实际价格(Y)范围内波动的,这意味着预测是有效的。
图7
表1
图8
图9
图10
图11
图12
三、结论
这部分主要研究了当前金价水平和其历史价格的关系。首先通过取对数和一阶差分的办法使数据变得平滑。在得到稳定的时间序列数据后,我们找出了最小的AIC值,确定了AR和MA的阶数,建立了ARMA模型。之后进行了诊断检验以确定残差为白噪声。最终,我们预测了未来黄金价格的波动趋势并确定预测结果是有效的。
参考文献:
[1]Brooks,C.,2008.Introductory Econometrics for Finance.2nd ed. Cambridge: The University Press.
[2]Peng XiaoShu,Zhang Desheng,Wang Ruoxing,Chen Cong.2011. GARCH forecast model of international gold price considering exogenous variables. School of Science,Xian University of Technology.
[3]Eviews 5.0 Command and Programming Reference, Quantitative Micro Software, 2004.
作者简介:胡楠(1990.11- ),女,汉族,河南省洛阳市,硕士研究生学历,现就职于西南证券有限公司天府大道营业部,研究方向:金融学