精设问题 有效互动 发展素养

吕翠仪

【摘要】课堂教学中生生、师生之间的有效互动，能提高学生数学思维能力，促进数学核心素养的形成。本文以“指数函数图象与性质”的教学为例，阐述在课堂上通过精心设计研学问题，引导学生合作交流，理解数学知识本质，是提高学生数学思维能力，促进学生数学素养的有效途径。

【关键词】研学问题   互动交流   数学素养

白益民教授认为：课堂教学中师生的实质性互动行为是有效教学成效的基础。在研学后教的理论指导下，师生之间，生生之间的互相交流明显增多，但是，如何实现有效的互动，仍是教师关注的问题。本文以“指数函数图象与性质”这一节课为例，谈谈在高中数学课堂上师生如何实现有效互动，从而提升学生的数学学习兴趣，发展学生的数学素养。

1.教材解读

“指数函数图象与性质”是2019年人教A版必修一教材第四章第二节指数函数的第二课时，学生在初中学习过一次函数与二次函数，在这节内容之前，通过图象直观研究函数性质，也学习了“幂函数”，初步理解了研究一类函数的过程与方法。

本节引导学生类比学习幂函数的过程，去研究归纳指数函数图象与性质的过程。在教学过程中注重问题的设计，语言的引导，小组的合作，从而达成有效的互动。

2.课堂教学策略

2.1 问题引导，启发思路

研学问题1：根据你学过的函数（一次函数，二次函数，幂函数），你认为研究一个函数的图象与性质的一般思路是什么？

师生在共同回答中补充完善下面的研究流程：

设计意图：通过问题，引导类比思考，形成基本的函数研究思路。

2.2 小组合作，寻找性质

教师给每一个学习小组一张表格纸，让学生们根据刚才的回忆与分析，互相讨论选择画那些特殊的指数函数的图像。

设计意图：从图象直观感知图形变化规律，是数形结合数学思想的体现。让学生自己经历选函数作图象的过程，有利于发展学生的感性认识。学生的讨论选择，也可以让学生认识到自己的理解是否全面。

学生作完图形后，引导学生思考回答下面的问题。

研学问题2：通过图形，我们应该研究指数函数哪些性质？这些性质是否具有一般性？指数函数的图象有没有特殊之处？需要分类讨论吗？

设计意图：启发学生从函数的一般性质：定义域，值域，单调性，奇偶性等方向进行研究，并考虑特殊情况。

2.3 展示交流，共同归纳

以下是两个小组展示的图片。

小组成员选择的特殊函数不一样，得出的结论就有差异。

教师通过几何画板的演示，给出以下函数的图象，引导学生归纳性质。

设计意图：通过对比，学生能够找到自己研究知识的不足之处，从而意识到从特例到一般的研究过程，要多思考各种不同的情况，使研究更全面。这种方式的互动有利于学生对指数函数知识理解得更透彻。

研学问题3：你还能从这几个不同底数的函数图象中找出什么规律？

通过几何画板的演示，引导学生比较底数大小与图象位置的关系;比较底数互为倒数的两个指数函数的图象的特征，从而更全面的认识图形。

研学问题4：不进行描点，你能在你所画的图形中把函数y=ex与y=（    ）x的图象画出来吗？

设计意图：先从图象出发，让学生寻找底数不同的指数函数的图形位置规律，从感性认识上升到理性认识。再从理性认识到感性认识，寻找其它指数函数的图象，发展学生的直观想象能力。

2.4 知识应用，生生互教

师生根据图象直观归纳出指数函数的性质后，初步进行知识的应用。

1.比较下列各组数的大小

（1）1.52.5，1.53.2;                 （2）0.6-1.2，0.6-1.5

（3）（     ）1.8，（     ）0.8     （4）1.70.2，0.92.1.

2.函数y=ax-2+1（a>0且a≠1）的图象必经过点（）

A.（0，1）      B.（1，1）    C.（2，0）     D.（2，2）

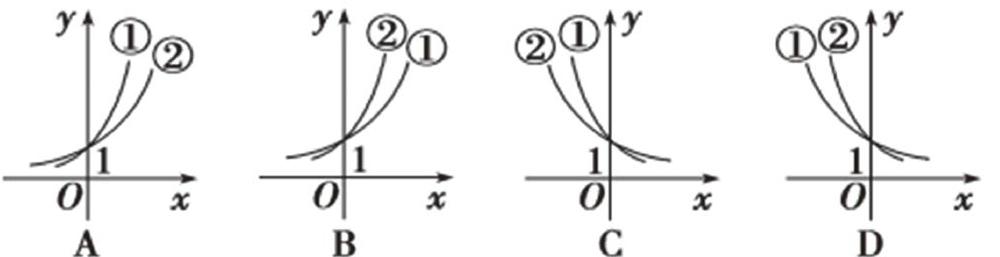
3.已知1>n>m>0，则指数函数①y=mx，②y=nx的图象为（）

学生个体先独立思考，然后小组成员互相讲解，最后，教师归纳方法。

设计意图：通过三种不同类型的问题，检验学生是否理解知识，能否用函数的思想去解决数值大小比较的问题，能否借助图象帮助理解，渗透数形结合思想。

2.5 课堂小结，突出思维

研学问题5：本节课你有什么收获？用到了哪些数学思想方法？

设计意图：引导学生思考自己在课堂上学会了哪些知识方法，学会总结与反思。

3. 教学反思

3.1 精心设计研学问题，促进生生、师生互动

课堂教学中，学生之间，师生之间的互动需要问题引领，师生思维的碰撞只有在问题解决时才会出现。故此，教师应根据教学内容，根据学生已有的认知水平，在学生思维的最近发展区中设计问题。研学问题的设计要有一定的思维度，有一定的开放性，能激发学生学习兴趣，也能给不同层次的学生有思考的空间;还要体现数学知识的本质，体现数学研究的本质。

本节课精心设计了五个研学问题，从类比学过的函数的研究方法出发，逐步引导学生通过选择特殊函数，画出图象，归纳图象特点，得出一般结论。根据研学问题，学生有目的的进行了充分的交流，从而实现生生，师生之间的有效互动。

3.2 注重知识形成的发现，提升数学素养

数学家弗赖登塔尔认为：学习数学的唯一正确方法是实行“再创造”。也就是由学生本人把要学的东西自己去发现或创造出来;教师的任务是引导和帮助學生去进行这种再创造的工作。

本节课注重学生知识的“再创造”的过程，围绕着如何寻找指数函数的图象与性质展开研究，让学生通过动手操作，合作交流，展示归纳等发现指数函数的图象分类与特点规律等，让学生有效经历研究指数函数图象与性质的完整过程。在整个学习过程中，教师重视学生互动交流的设计，鼓励学生展示自己的发现成果，引导学生深入思考自己思考问题的不足之处，重视学生数形结合思想的形成，从而提升学生数学抽象，直观想象等素养。

总之，教师在课堂教学中，应注重数学知识的本质，精心设计研学问题，促进生生，师生的有效交流，让学生在合作交流中理解知识，发展数学思维能力，实现数学核心素养的提升。

【参考文献】

[1] 白益民 高成效教师行为特征研究[J]，教育研究与实验，2000（4）

[2] （荷兰）弗赖登塔尔著;陈昌平 唐瑞芬等编译 作为教育任务的数学[M]，上海教育出版社，1999