基于“错误资源”利用的“体验式”数学纠错的策略研究

□陈 琳

（杭州市余杭区乔司中学，浙江杭州 311101）

美国著名教育心理学家桑代克运用实验提出：“学习的过程是一种渐进尝试错误的过程.”[1]在这个过程中，无关的错误反应逐渐减少，而正确的反应最终形成.而体验学习的提出者大卫·库伯则认为学习的过程应该是体验、反思、概括、应用这样的四个阶段循环往复组成.在分析学生的错误时，正面的灌输未必有效，而通过学生自我尝试甚至犯错误而体会到的，将更具体验性和亲历性.因此教师要善于利用错误资源，使学生从中审视体验，继而有目的地引导学生自己产生问题，自己解决问题.本文就数学课堂教学中错误资源的“体验式”纠错教学策略的实施谈谈自己的做法.

恩布里奇曾说过：“差错人皆有之，只有大量错误作为台阶才能攀登上正确结果的宝座.”教师要正视错误资源的价值，通过合理利用使学生的错题“来源于学生，服务于学生”，要有效利用错误，必须要清楚学生“错误”背后的真实想法.

一、暴露学生真实的想法 体验“意料”之错

（一）有意制造“错误”

新授课时，一些教师会把数学概念以快而直接的方式教授给学生.这样的处理方式会将学生对新概念的一些错误认知隐藏起来，学生没有能够在课堂里体验到.心理学家盖耶认为：谁不愿意尝试错误，不允许学生犯错误，谁就将错过最富有成效的学习时刻.“课堂就是让学生出错的地方.”[2]所以，教师往往需要预先设计一些“错误”，让学生适时地在“体验错误”的过程中，暴露出原先隐藏的一些错误想法，从而帮助学生自发地发现错误和解决错误.

1.预设错误（浙教版七年级下册第5章分式的第一节）

例1下列代数式中，哪些是整式？哪些是分式？

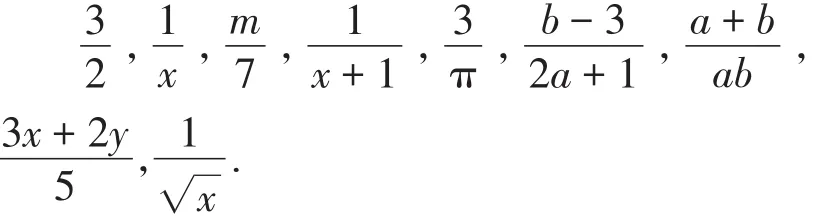
（经过一段时间的思考）

师：同学们有不同的答案吗？

师：还有不同意见吗？

通过“预设错误”的环节，笔者从学生熟悉的整式入手，引导学生从旧知中发现新知，这样的设计符合学生原有认知水平，有利于探索活动的展开.在这其间，通过师生之间的对话，笔者明白学生对于整式和分式已有了较好的区分度，但在预习的过程中，对分式的概念依然是一知半解，只知道分式只要分母中含有字母即可，而忽略了分式的分子和分母都必须是整式这一特征.通过一个“预设错误”环节的开展，学生的错误想法自然而然地从他们嘴里说出来.这时教师可以迅速调整自己的教学计划，明确本节课的重难点，提高课堂效率.

2.教师出错

传统的教学方法是教给学生正确的答案，而新课标要求教师要培养学生的问题意识.所以教师在一定程度上的“故意出错”，可以引发学生更加深入的思考并敢于发表自己的想法，从而全身心地投入到学习活动中去.除了课堂教学过程中的故意出错，在课后作业批改时也可以“故意批错”.当然需要注意的是“教师出错”并不是无时无刻都可以开展，否则会适得其反.

（二）有意诱导犯错

学生的思维是隐藏的，诱导错误是指教师根据学生的认知规律，诱导学生因学习负迁移去犯错，然后引导学生通过“探究”活动，从错误的观点中走出来.

例2已知等腰三角形三边的长分别是4x-2，x+1，15-6x，求这个等腰三角形的周长.

生1：周长是13.

生2：（马上举手）周长是12，13或者是12.3.

师：你是怎么思考的？（这个时候很多学生开始跃跃欲试，试图帮生2回答问题）

生2：此题中等腰三角形没有明确底和腰，要进行分类讨论，第1种4x-2为底，第2种x+1为底，第3种15-6x为底，通过计算后就有三种情况.

生2讲完之后，不少学生都点点头.笔者知道学生关注的点是在等腰三角形的分类讨论上，思维受阻，而忽略了构成三角形的三边的关系，所以当生2交流完毕后，没有学生提出异议.

师：刚刚同学们讨论得很精彩，那么也就是说，通过计算，三边是2，2，9，周长是13；三边是6，3，3，周长是12；三边是4.8，2.7，4.8 ，所以周长是12.3，是吗？（笔者故意将两位学生总结的答案写在黑板上，并且写上这个等腰三角形的周长就是13或12.3或12，并在三角形这三个字下打上重点号）

生4：（注意到了）我认为这个等腰三角形的周长只有12.3.另外两种情况都不能构成三角形.∵2+2＜9，不能构成三角形，∵3+3=6，也不能构成三角形.

显然，一开始生1掉入两个陷阱，既没有考虑到计算等腰三角形的边时的分类讨论，又忽略了三角形构成的条件.这个时候，教师可以因势利导，选择其中一个误区开始诱导，之后学生明显意识到本题需要分类讨论，慢慢地走出第一个误区，却还沉浸在第二个误区.然后，教师应该继续按照学生的思维出示答案，在强调学生的错误答案的同时，让学生又一次经历“错误”体验，在这个体验的过程中，师生之间共同交流，生生之间共同探索，从而得出正确的结果.这样的方式远比教师在生1回答完之后，直接抛出答案要好太多.教师有意诱导，学生就不太会出现“顾此失彼”的情况了.

二、暴露学生真实的想法 体验“意外”之错

课堂教学是动态生成的，它不是教师完全预设的.美国教育家布鲁己克曾说：“最精湛的教育艺术，遵循的最高准则，就是学生自己提出问题.”因为问题是自主探究的出发点，这些问题便生成了“意外”之错.这时，教师应因势利导，让学生在误中思，思中悟.

（一）有意将错就错

将错就错指的是事情已经做错，就顺着错误继续做下去.有的时候教师不妨将错就错，“以疏代堵”让学生自己去选择解决问题的途径.

例3在讲解浙教版七下第5章《分式的化简》的时候，有这样一类题目：

师：错在哪里？

生2：它在解方程（一针见血）.

显然，对于分式化简，学生经常会犯这样的错误.从生1分母和通分搞混来看，与其说是搞混，不如说是没有真正理解等式的基本性质.学生的错误已经根深蒂固，这个时候不如将错就错，按照生1的方法操作下去.

之后，大家一致决定给生1再一次机会上黑板来解决问题.这个时候，生1信心倍增，胸有成竹地上黑板做解答.

他的解答过程如下.

这样有意地将错就错，适时地为生1创造能正确解题的条件，同时，也让该生能将两个式子进行形象而且清晰的对比，学生用他自身的眼睛进行有效体验，感知到两个式子的不同，显然比枯燥贫乏的“这样写就错了”，或者是“这不是方程”的字眼要好很多.

（二）有意变式追错

变式追错是指在教学的过程中，教师讲评完之后，可以继续巧妙地设置相关的错题.通过变式的追踪帮助学生真正理解问题，找到方法.

在讲授浙教版七下第4章《因式分解》的时候，时常会碰到学生因式分解不彻底的情形.

例4将多项式-3mx2+12ma-9m因式分解.（学生上黑板板演）

生1：-3mx2+12ma-12m=3（-mx2+4ma-4m）.（很显然该学生将系数3提出来了，这个时候，教师笑而不语，反观其他学生的表现）

在这个过程中，学生的话令笔者印象深刻.学生对提出“负号”的理由，仅凭“记忆”，可见有的时候学生题目做对了，可能是真会，有的时候学生题目做对了，可能并不是真会.之后笔者又设计了例如将6am-3am2-3a因式分解的练习.

变式1：将6am2-3am4-3a因式分解

生1：老师，我想要到黑板上来板书（.一副胸有成竹的样子）

笔者赶忙请他上来.他写得很快，笔者知道刚刚他听得很清楚.

不知道作为教师的我们是不是时常会碰到刚刚这样的场景，前脚刚讲过，后脚又出现同样的错误，又没有分解彻底.这个时候，很多教师肯定会说出“我才讲过，你有没有认真听？”这样埋怨的话.其实回过神来想想，在这个时候说这样的话，一个毫无意义，另一个就是打击了学生展示自我的积极性.生1是胸有成竹地上来的，我们不能一盆冷水泼到他头上去.

于是笔者不紧不慢，没有立马指出该生的错误，而是让学生再观察观察：该式还能不能继续因式分解？

生2：（好像还可以，但不是特别有把握）解答过程如下：

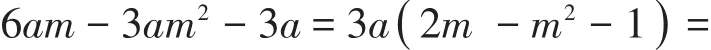
虽然生2做对了，但笔者没有立马肯定他的做法，因为笔者在他脸上看到了疑惑.他的疑惑应该不是答案对不对，而是负号可不可以提出来.

笔者适时抛出问题：同学们，你们觉得他做得对吗？

这个时候，笔者只听到学生小声地说出来：好像是对的.远没有一开始的胸有成竹.

生3：老师不是说过只有首项是负号的时候才能把负号提出来吗？

这个问题的出来，达到了笔者设置此变式的目的.学生的困惑在于此.这个困惑在原题中并没有呈现，因为它被正确的结果所掩盖，而在此题的解决过程中却暴露了问题的存在.

生4：要把负号提出来的目的主要是为了更好地因式分解.首项为负的时候，通常选择把负号提出来，也是因为能更好地因式分解，在本题中只有把负号提出来，两个平方项才是正数，才能因式分解.

学生纷纷做点头状，笔者也给予生4的话高度认同.同时，笔者补充道，数学的记忆是理解的记忆，要真正悟其道，才能以不变应万变.

所以在教学过程中，教师要随时用心去捕捉一些似是而非的错误，巧妙地设置相关变式，让学生隐藏在正确下的隐形错误现形，从而激发学生进行深入思考的激情.经历这样的探究过程，学生收获的不仅仅是因式分解的方法，更是观察分析等学习能力的体验.

三、整合错题 促进学生“触类旁通”

学生从“错误体验”到“正确体验”必然是一个漫长的过程.为此，对于学生学习过程中的错误不能单纯“就题论题”，以为这个问题解决了，相关的问题就能解决了.在日常的教学过程中，经常会碰到学生这题会了，类似的下一题又不会了.一个原因可能是学生并没有真正理解原题；另一个原因是单个题目、单个知识点的讲解，对于学生而言“体验错误”或者“体验正确”都过于单一和单薄，并不能很好地形成知识网络或题型网络.所以，教师还应该帮助学生对同一类型的“错题”做有效整合，从而促进学生“触类旁通”.

例5如图1，在△ABC中，∠ABC、∠ACB的平分线交于点O，∠BOC与∠A的关系是___.

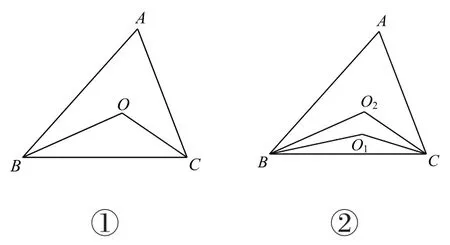
图1

在本题讲评完之后，笔者并没有“讲完就完”，而是预先设计了相关变式拓展.

变式拓展：已知：如图2，在△ABC中，BP平分∠ABC，CP平分∠ACD，根据以上信息回答下列问题：

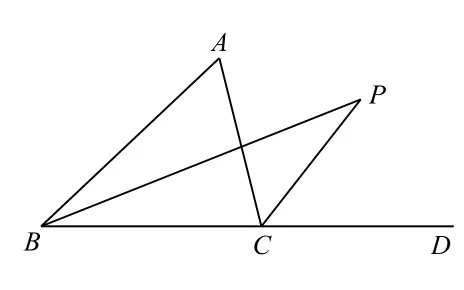
图2

（1）∠A和∠P的数量关系为________.

（2）如果∠ABP=20°，∠ACP=50°，则∠A+∠P=_____．

（3）如图3，在△ABC中，BP1平分∠ABC，CP1平分∠ACD，BP2平分∠P1BC，CP2平分∠P1CD，…

图3

则∠Pn与∠A的数量关系为____.

很明显，在教学中，面对学生的易错点和易混点进行及时的归纳整合是非常有必要的.在教学过程中，合理的设置变式能将原本单个的知识点或方法串成一条线.学生通过心中“线”的指引，提高了解决问题的能力.

综上所述，在初中数学纠错教学中，“体验式”纠错的策略，既强调了学生在学习过程中的亲历性和感受，也注重知识结果的收获.它能引导学生从被动学习到主动学习，自主地接受“错误”的体验，在“体验”错误的过程中，自发地去解决问题.

错误就似一场意外的邂逅，它让学生在“过河”后没有找到正确的“道路”.“路”必须让学生自己走，如果走错了，教师要引导学生，使他们回到正确的方向，继续前行.最后用一句话结尾：眼前有人易喜易嗔，给它好风好水，让它好花生长 .