指向生成的数学单元复习课教学*

□任宏章 周正峰

（南京师范大学苏州实验学校，江苏苏州 215100；苏州市相城区教育发展中心，江苏苏州 215100）

单元复习课不能是简单的知识点的回顾，解题方法的重复.如何才能够上出新意？

对教者而言，怎样设计问题？怎样选择题目？怎样在问题背后挖掘学科思想方法？对学生而言，如何学出新意？学出兴趣？提升思想认识？理解问题更胜一筹？我们以全面性理解、开放性思维为课堂设计和课堂教学思考的着力点，以课堂生成为指向，关注教学的过程，不断地留意学生的变化和反应，捕捉偶发的智慧火花，并对学生的反应做出积极的回应.

以一元一次方程的单元复习为例，我们确定教学目标如下：①通过基础练习，增强对一元一次方程相关概念的理解，激活解一元一次方程和建立一元一次方程模型解决实际问题的经验，自主构建一元一次方程的单元知识体系；②通过典型例析，深入领悟解一元一次方程的化归思想方法，强化建立一元一次方程模型解决实际问题的经验，自主提高综合分析问题和解决问题的能力；③通过拓展训练，进一步升华解一元一次方程和建立一元一次方程模型解决实际问题的经验，自主提升创新解决问题的能力.教学重点是深刻领悟解一元一次方程的基本思想和提升利用一元一次方程解决实际问题的能力．

这里目标指向明确，分别以基础练习、典型例析、拓展训练串联预设复习课教学的全程，下面具体说明在实际教学过程中如何以全面性理解、开放性思维为课堂设计和课堂教学思考的着力点，以课堂生成为指向进行课堂设计和课堂教学.

一、凭借问题，激活经验，全面理解，构建数学知识体系

以问题为出发点，提出相关的问题，学生依据问题进行知识的梳理，实施知识点的再现、理解和运用，激活已经积累的运用数学知识的经验，构建数学知识体系.

【环节一】凭借问题，课前感悟

（1）本章的主要内容是什么？

（2）什么叫一元一次方程？其标准形式是什么？它有几个解？

（3）等式性质内容是什么？

（4）解一元一次方程的一般步骤是什么？每一步的依据是什么？其解法体现的基本数学思想是什么？

（5）列一元一次方程解应用题的一般步骤是什么？解题的关键是什么？

课堂开始先让学生分组交流课前预习情况，然后由小组推选代表全班交流.对于问题（1），不同层次学生有不一样的感受，有的学生回答学习了解一元一次方程，有的学生说学习了一元一次方程的解法和运用，有的学生说学习了一元一次方程的概念、解法和运用，有的学生进一步补充利用方程思想解决实际问题.可以看到不同学生对学习内容的理解深度不同，感悟有差异，也就是说生成有差异，但都是在问题串的引导之下，开始逐步完善、全面地理解问题，在不断地生成过程中构建知识体系，原先认识问题不全面、不充分的学生，在同伴的启发之下对问题有了全面的理解.优秀的学生把下面的几个问题联系起来理解，问题（1）的回答就隐含在下面几个问题之中，问题（2）（3）（4）（5）就是问题（1）的具体化.

对于问题（2），在“有几个解？”上，出现不同的声音，有的学生认为可以有一个解，或者无解，或者有无数个解.马上有学生提出，概念中未知数的系数不为0，只能有一个解.这时教师再引导学生深刻理解一元一次方程的概念，充分肯定后一个学生对问题的深刻领悟，通过对未知数的系数的分类探讨，未知数的系数不为0是一元一次方程，有唯一解，而系数为0时不是一元一次方程，又分为两种情况，一种情况无解，另一种情况有无数个解.至此，学生的思维在不断生成中发展，学生对问题有了更全面更深刻的理解.

对于问题（3），突出说明等式性质是为解方程服务的，是方程变形的重要依据.对于问题（4），强化步骤，强化依据，强化化归思想，解方程的目的是将方程化归为x=a的形式.对于问题（5），关键是建立一元一次方程的模型，通过解一元一次方程实现问题的解决.

【环节二】基础练习，激活经验

1.下列是一元一次方程的是（ ）

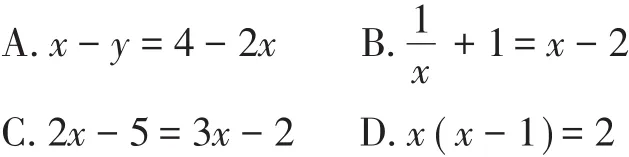
2.已知方程（a-2）x|a|-1=1是一元一次方程，则a=______，x=______．

3.如果x=-2是方程-3x-4=k+1的解，那么的值是____.

4.x=-2是下列哪个方程的解（ ）

A.-2x+5=3x+10

B.-3(3x-2)-5=19

C.5x-3=6x-2

D.4x-3(20-x)=6x-7(9-x)

5.下列解方程去分母正确的是（ ）

7.某班分两组去两处植树，第一组22人，第二组26人.现第一组在植树中遇到困难，需第二组支援.问第二组调多少人去第一组才能使第一组的人数是第二组的2倍？

设抽调x人，则可列方程（ ）

A.22+x=2×26

B.22+x=2(26-x)

C.2(22+x)=26-x

D.22=2(26-x)

8.一项工作，甲队独做10天可以完成，乙队独做15天可以完成，若两队合作完成这项工作，需要的天数是（ ）

A.25 B.12.5 C.6 D.不确定

问题1、2，提供了深度理解一元一次方程的概念的机会.问题1是形式上的领会，能够转化为ax=b的形式，问题2是本质上的认识，强化指数为1，未知数的系数不为0，是学生原有知识的激活、再现和深悟.

问题3、4，提供了深度理解一元一次方程的解的概念的机会.一元一次方程的解是使方程左右两边的值相等的未知数的值，验证方程解的方法就是把未知数的值代入方程左右两边，看值是否相等，同样是原有知识的激活、再现和深悟.

问题5、6，在教学过程中，教者追问各个步骤实施的依据和注意点，激活了学生解一元一次方程的经验，加深了对解一元一次方程的思想方法的理解，加深了对容易错误之处的理解.在解决问题6的过程中，一名学生采用两边通分的方法，分母相同时分子也相同的比较方法解题.对于这一节外生枝的情况，教者充分肯定了学生的做法，给予了表扬，事实上后面学习分式方程解法时，这是一个重要的思想，保护学生思维的火花就是保护学生的创新思想.在肯定学生的同时，教者让学生比较不同的解法，让学生在比较中发现更好的做法，这是求简，更是审美.

问题7、8，通过建立一元一次方程的数学模型，激活了学生建立一元一次方程模型解决实际问题的经验，找相等关系是解决问题的关键，选取未知数表达量关系是建立方程的关键.如何设未知数，用未知数的代数式表示相关量，根据相等关系建立方程，列一元一次方程解决问题，变得有路可寻、有法可依，目标明确，思路清晰.

二、典型例析，开放思维，加深理解，感悟数学思想方法

数学知识点相关的题目很多，不加选择地拿来，可能会重复，可能会不落重点，可能会难度过大.我们需要精心选题，落实重点，开放思维，突出思想，在不断地生成中加深对数学概念、性质和法则的理解，感悟数学思想方法.

【环节三】典型例析，感悟方法

9.解下列方程：

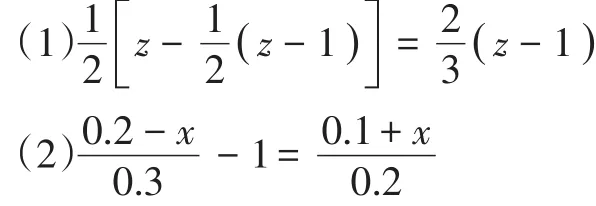
10.两支同样长但粗细不同的蜡烛，点完一支粗蜡烛要2h，而一支细蜡烛只能燃1h.一次晚上停电了，小静同时点燃了这两支蜡烛看书，来电后同时熄灭，小静发现粗蜡烛长是细蜡烛的2倍，问停电了多少分钟？

问题9，提供了开阔的思维空间.实际教学过程中，对于方程（1）学生提供了多样化的解法，有的先去括号，再去分母，有的连续两次去分母，有的学生注意到两边同乘以2后，发现（z-1）先整体移项合并，等等.方程（2）的通常解法是先利用分数性质化去各个分数形式部分分子、分母中的小数，转化为分子、分母不含小数的方程，然后按常规步骤完成.实际解题过程中，有学生把分数形式部分分离成为两项，小数自然化去，也有学生两边直接乘以0.6去分母，变成含小数而不含分母形式.学生的思维开阔，思路众多，方法灵活，充分展现了思维的开放性、课堂的生成性.但不管是哪种方法，目标都是化归为x=a的形式，通过训练、比较、感悟，加深了对解一元一次方程的化归思想方法的理解.

问题10，容易找到相等关系：来电后同时熄灭，粗蜡烛长是细蜡烛的2倍.但如何来表示？

原来蜡烛的长度未知，许多学生不知道怎么办.教者让学生分组讨论，小组内对话，互相启发，马上有小组提出引进参量，假设蜡烛长度为a，设停电x分钟，问题似乎解决了.解表示出来的方程，发现参数a消失了，很令人兴奋.还是解不出来，再找原因，发现单位没有统一，统一单位后终于可以解出来了.问题解决的过程中不断生成新问题，促进思维向纵深发展.此刻，教者进一步引导学生回顾解题过程，再反思，发现参数a可以假定为单位“1”，这样方程中只有一个未知数，直接得到我们熟悉的一元一次方程，优化了解题过程.生成、发展成为课堂解决问题的主旋律，问题10的解决强化了建立一元一次方程模型解决实际问题的经验，提高了综合分析问题和解决问题的能力.

三、拓展延伸，生成发展，升华理解，形成创新思维能力

思维要引向深入，学习才会变得更有意义.为了未来的智慧而学习，数学学习创设拓展延伸的问题，让学生的思维开放、思路开阔，在变化中求发展，就能升华学生对数学思想方法的理解，形成创新思考数学问题的能力.

【环节四】拓展训练，提升思想

11.小丽在解方程5x-1=□x+3时，把“□”中的数字看错了，解得x=2，那么小丽把“□”中的数字看成了____．

12.甲、乙两班学生到集市上购买苹果，苹果的价格如下：

购买苹___________果数每千克___________________________________________价格不超过30千克______3元30千克以上但不超过50千克____2.5元50千克以上__2元

甲班分两次共购买苹果70千克（第二次多于第一次），共付出189元，乙班则一次购买苹果70千克.

（1）乙班比甲班少付出多少元？

（2）甲班第一次、第二次分别购买苹果多少千克？

问题11，一方面检测学生对方程解的概念的理解，2是使方程左右两边的值相等的未知数的值.另一方面，当我们把2代入方程时，方程变为10-1=2□+3，实质就是关于“□”的一元一次方程，要求学生用变通的思想解决问题.问题11的解决是容易的，但要让学生感悟变通，善于用数学的眼光、变通的思想审视问题，从简单中感悟到思想的重要.

问题12，首先是阅读理解，要能够读懂表格，价格按区间定位表示，这跟经验中的分段定价表示是不同的.乙班一次购买苹果70千克，都是按每千克2元计算，只要2×70=140元，乙班比甲班少付出49元，阅读理解过关，问题（1）即可解决.问题（2）有学生直接按第一次不超过30千克，第二次30千克以上但不超过50千克计算，得出第一次购买28千克，第二次购买42千克.教者追问：这样做符合要求了吗？很快引发学生的深刻思考，再次让学生分组讨论，马上有一个小组提出自己的理解：也可能第一次不超过30千克，第二次50千克以上；也可能第一次30千克以上但不超过50千克，第二次50千克以上.马上有另一个小组反对说第二种情况不可能，否则超过70千克了，全部学生立刻会意.接着有学生发言：会不会两次都是30千克以上但不超过50千克？马上有学生说这不可能，否则应该付出175元.至此，教者提出：究竟应该怎样思考呢？于是学生经过讨论一致认为：分类探讨，排除不可能都不超过30千克，也不可能都在30千克以上但不超过50千克之间，更不可能都在50千克以上，也不可能是第一次30千克以上但不超过50千克，第二次50千克以上，这样只要列方程求解两种情况：①第一次不超过30千克，第二次30千克以上但不超过50千克；②第一次不超过30千克，第二次50千克以上.结果发现只有一种情况存在.问题12的解决，是开放性思维的结果，在问题探索过程中不断地深入，不断地生成，不断完善认识，系统地思考问题.

课堂总结仍然先小组内归纳总结，然后派代表班级交流，小组内其他成员可以补充，再由其他小组成员补充.一个小组成员说本节课复习了一元一次方程的概念、解法和运用，对于方程的概念注意三点：一元、一次、整式.马上本组其他成员补充一元一次方程的解法步骤，并说明了各步骤的注意点，补充说明建立一元一次方程解决问题的基本思路.再后来，其他小组成员补充说明解一元一次方程的基本思想化归为x=a.课堂小结在生生的对话过程中不断完善，不断引向深入，可以说是学生自己建构了一节课小结体系，思维活跃，全面深刻，是真正意义的全面了解、系统思维.

最后，再一次反思以全面性理解、开放性思维为课堂设计和课堂教学思考的着力点，以课堂生成为指向的单元复习课教学.首先，深刻领悟教材与学生，教师在全面理解教材的意图基础上，结合个人的理解，对复习的内容进行取舍，确定教学重点，再考虑到学生的知识基础、学生的学习心态和学生的学习能力，把教师的理解怎样转化为教学行为，教者给予学生足够的时间和空间，让学生有充分的对话表达，通过学生的亲身经历、感受感悟、激活经验、唤起兴趣，思想碰撞产生灵感，不断生成求得发展.其次，凭借设计的数学问题，通过情境的创设，引导学生有高度、有深度地思考问题，把已学的知识进行再现、整合和发展，通过精心设计范例，开放思考问题，在充分展现通解、通法的基础上，力求能够从多个角度思考问题，寻求一题多解、一法多用等.再次，教学过程充分揭示数学要素之间的本质联系，强化数学思想内涵，充分揭示数学问题中的对象关系，多角度地思考问题，强化数学的理解，不同寻常的发现，在变式拓展问题、培养解题能力的同时获得心灵的震撼、学习的兴趣和智慧的发展 .