简谈思维的培养

江苏启东市南苑中学(226200)李卫星

江苏启东市折桂中学(226200)顾向红

思维是人脑对客观现实的概括和间接的反映,反映的是事物的本质及内部的规律性.是一个长期积累的过程.因此分析问题解决问题的思维方法,是很难通过一两道题就掌握的,需要很长时间的锻炼和反思、数学学习中需要进行判断与决策的地方远远多于我们的想象,可以说,数学学习的过程就是解决问题的过程.而大脑是解决这些问题的唯一工具.要正确利用这个工具,这就涉及思维的某些概念,诸如本质,方法和运作.正确的思维方方法,是一切高效学习的基础.解决问题的核心就是思维方法灵活自然地运用.人类在思考问题的过程中,自身的思维习惯、性格、知识积累无不都在悄悄地影响着思维的过程,要克服某些不良影响,得到积极影响.这就要求我们在平时的教学当中,我们进行具有足够深度的总结和提炼.根据笔者多年的教学经历,发现如果只是练一题讲一题,或者讲一题用多种方法,而不再一个问题上纵向深入,是很难达到好的效果的.顺着这个教学思路,笔者将思维的培养分成个运作的方向分成3 个,这3 个不同的思维方式,既是相互独立,也是相互联系的.笔者将以两道典型题为例,阐述如何根据这3 个不同的方式解决具体问题.同时也会通过这两道题阐述四种思维方式之间的对立统一关系.

第一点：寻找逻辑立足点,多角度思考,殊途同归,开拓视野

很自然地,问题出现了,那就是我们应该怎样思维? 从最不严谨的角度说,思维是一系列问题我们曾经出现的想法,从这个角度来说,任何人任何时刻都在思维.但是仅仅是一些类孤立而且毫无头绪的思索,是无法成为有意义的思维活动的.因此从思维的实用性来说,有序连贯,带有目的性,有立足点的思考才是真正的思维活动,否则仅仅是“想”而已.但是每个学生的逻辑出发点是不同的,学生的知识掌握程度也存在客观差距.所以,每个人的思维活动也是多样性的,这种多样性即来自于逻辑的立足点的不同.既然每个人对问题都有不同角度的看法.那么利用逻辑出发点的不同解答疑惑,将是一种良好的方法.

如图,AB为⊙O直径,D是弧BC的中点,DE⊥AC交AC的延长线于E.

(1)求证：DE是⊙O的切线;

(2)若DE=3,⊙O的半径为5,求AD的长.

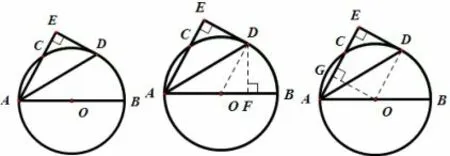
学生A：连接DO,并过D点作DF⊥AB.因为是BC中点,所以∠EAD= ∠DAB,所以AD是角平分线,所以ED=DF,所以DF= 3.因为半径为5,所以OD= 5.因为∠DFO=90°,所以DF2+OF2=DO2,32+OF2=52,OF= 4.因为AO= 5,OF= 4,所以AF= 9,因为∠DFA= 90°,所以DF2+AF2=AD2,32+92=AD2,AD=

解析学生A 从角平分线上出发,目的是让各个分散的条件整合起来,使其能够在我们的解题范围内.由角平分线引发“角平分上的点到角两边的距离相等”,过D点做垂线,在利勾股定理即可证得.

学生B：连接OD,并过O点作OG⊥EA.因为ED为DO切线,所以ED⊥OD,所以∠EDO= 90°.因为DG⊥EA,所以∠AED= 90°.因为四边形EGOD是矩形,所以ED=OG= 3,EG=OD= 5.因为∠AGD= 90°,所以AG2+GD2=AD2,AG2+32= 52,AG= 4.因为AG= 4,EG= 5,所以AE= 9.因为∠AED= 90°,所以AE2+ED2=AD2,92+32=AD2,AD=

解析学生B 同样是为了将条件整合在一起,但出发点不同.他从90°出发,利用矩形巧妙的实现转换,一样达到了目的,采用勾股定理即可证得.

这道题的两种解题角度,并不是想说明这两种思维方式水平高低,而是显示这样一个道理：思维是立足于某种根据的东西.在数学题中,这个根据可能是一个直角,一个定理.如果我们在解题陷入误区和障碍,并且花费大量时间时,我们要做的就是快速的转换角度.从其他条件入手,重新审题.假设在选取角平分线法(方法A)解答问题时,陷入障碍无法解答,那么他可以重新审题,将目光转到直角上,快速切换思路.这里还是要强调,并不是每个学生在将注意转移到直角上就能得出B 的结论,我们承认学生间知识掌握程度的客观差距,任何解决问题的过程都是以先验的东西为前提,经大脑整合提炼的.但是知识掌握程度不好的同学,还是可以尝试此法,用以开拓思路.

第二点：脱离问题本身,引导思维向更深处发展

心理学认为,人都不可避免的受着各种各样的偏见的影响,这些偏见就是我们常说的“思维定势”.思维定势并非完全有害无用,从思维定势的形成来说,他来自于我们的生活经验,因为具有一定的实际意义,才逐渐被我们接受,以至于成为一种定势约束我们的思维.

我们接着看上面那道题第三问.有学生C 的解答如下,他从方程思想的角度出发,得到正确的解答.在这里学生已经跳出几何题的束缚,高屋建瓴地看待问题,寻找普适方法：方程思想.这也是数形结合思想的另一体现.要做到这点,跳出几何的舒服,破除思维定势,与学生的自我调节和教师的传道授业都有关.教师的任务是传递各种信息,在平时的教学和评奖中,注意提示各种有效甚至有效但也许无用的信息,促进学生的独立思考,而学生要做的就是,在经过长期自我调节与约束,控制大脑的思考方式,这也符合思维形成的规律.自主提取信息并分析信息,结合学生自己的经验,接下让学生进行比较,逐步对比,分析依据,并同时展开讨论,“在死胡同中进行多次迂回探索,痛苦探索并快乐”.如果学生没有AB 的思路,大可以不要纠结于几何本身,而从大脑里寻找新信息.我们从这里可以得到一个结论：如果问题本身无法给我们突破,那么我们可以从问题之外寻找突破.

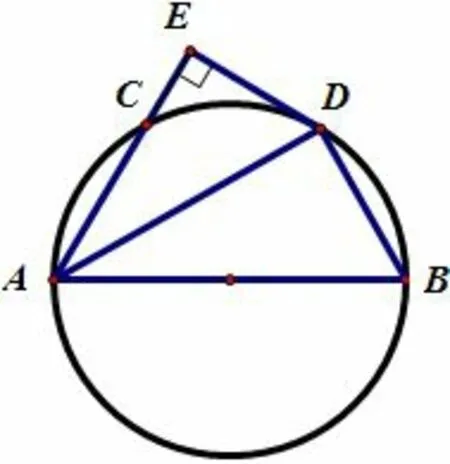
图2

学生C：连接DB.因为D是CB中点,所以∠EAD=∠DAB.因为AB是直径,所以 ∠ADB= 90°,所 以∠AED= ∠ADB.因 为∠AED= ∠ADB,∠EAD=∠DAB,所以△EAD～△DAB.设AD=x,因为∠ADB=90°,所以AD2+DB2=同乘x2,可得x4+ 900 = 100x2,x4-100x2=-900,x4-100x2+2500=1600,(x2-50)2=1600,x2-50 =±40,x21= 10,x22= 90,所以因为当时,∠EAB ＞45°,超出圆的范围,所以不符合,所以所以

第三点：从殊途不归在挖掘两点,反馈再思,积累方法

但是从人的习惯上来说,人类都是倾向于已经习惯的东西,经验的东西通常是人的第一选择.同时人的大脑的思维方式又存在多种路径,在习惯的驱使下,人就会下意识地选择经验,抵触细致的分析.从这个角度来说,思维如果存在多种捷径,将是有利也有弊.一方面,他提高了人的工作效率.而另一方面,笼统的看一个问题要比细致的分析简单得多,选择捷径也将降低人对问题的认知程度.也就是说,有时候时候,我们会殊途不归.这包括三种情况：逻辑立足点本身的错误,论据的缺乏与不足,以及解答者知识水平的限制.我们将通过下题继续说明这点.

(14 分)正方形ABCD边长为4,M、N分别是BC、CD上的两个动点,当M点在BC上运动时,保持AM和MN垂直,

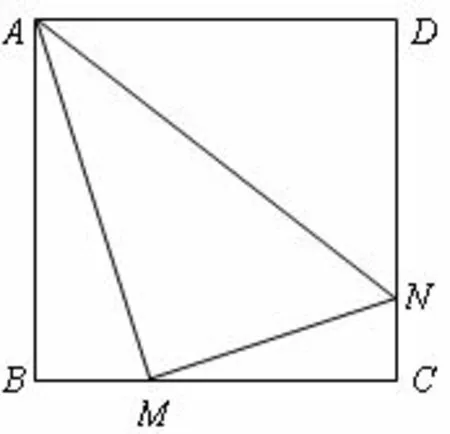
图3

(1)证明：Rt△ABM～Rt△MCN;

(2)设BM=x,梯形ABCN的面积为y,求y与x之间的函数关系式; 当M点运动到什么位置时,四边形ABCN面积最大,并求出最大面积;

(3)当M点运动到什么位置时Rt△ABM～Rt△AMN,求x的值.

学生A：因为Rt△ABM～R t△AMN,所以同 理由勾股定理得,所以

学生B：M为中点若相似X= 2.因为△AMN～△ABM,所以又△ABM～ΔMCN,所以所以所以BM=MC,所以BM=MC=2,所以M在中点.

解析利用三角形相似将两对三角形常规思维从角出发,利用垂直及角平分线的性质得出边的,求出点M.

学生C：过M作MF⊥AN于F,因为△ABM～△AMN,所以∠3 = ∠4,∠1 = ∠5.又因为△ABM～△MCN所以∠1 = ∠6,所以∠3 = ∠4,∠5 = ∠6,所以BM=MF,CM=MF,所以BM=MC=2,所以M在中点.

解析这种方法一度从边考虑常角形的中间△ABM抓住关系,通过的等效替换,得出各边的比等得出关系式求出M的位置M为中点,若相似X=2.

关于学生B 和C 的解答方法的不同,已经在第一点中阐明.学生A 建立方程但形成无理方程化成整式方程确实高次方程,是基于思维方法2 的跳出思维定势.然而无法解决,学生A 的方法确实不能解吗? 显然,从教师的角度来说,当然是可解的.因此学生A 的问题在于自身知识的限制.既然几何方法可以得到结论,学生A 代数方法也是可解的,我们是不是应该回顾解题过程,再次从代数方法中挖掘新的东西.

抓住思维的撞击点衔接点转接点,打破思考问题的封闭性,深化对知识理解,加深知识与方法的联系的认识,再次反馈原题,积累了新的方法,在本题就是整体思想.在别的题目中,可能是其他方法,足见沙漠中也是可以有绿色,殊途不归中也可以找到亮点.

总结培养“联系”的思考方式.

这里不再举新题目阐述,也不再阐述具体的方法.解题的方法和指导思想是多种多样的,任何一道题可能对应着很多解题方法,也对应着很多的解题思想,比如数形结合思想,分类讨论思想,方程思想等.同样的,思维方法也是种类繁多,比如逆向思维法,发散思维方法、收敛思维方法、求异思维方法、逆向思维方法、缺点列举思维方法、检核思维方法、纵向思维方法、横向思维方法、纵横向思维方法.然而这些让然离不开“联系”两个字,在解题中我们发现,任何方法的应用,不外乎是将几个知识点的联系后的优化.从中国古代的思想上来说,万物都处在相互的联系中,并非孤立存在.这个思想同样也在马克思主义哲学中提到,即任何事物都处于普遍联系之中,这就是联系的普遍性.联系的观点,不仅在自然科学,比如德布罗意发现物质的波粒二象性.也在人文社科领域有着重要的作用,比如银行利率的变动将导致人们消费意识的变化.

回到数学这个话题本身,学生要在数学上有一定的进步,学会“联系”的观点是必须的.任何学业上有所进步的人,总是有意识或者无意识地学会了“联系”.实施上,当我们解答完一道难题时,我们如果回顾题目,我们将发现,我们是不是将A 知识点和B 知识点结合起来,才得到了C 结论.虽然单独从A 或者B 我们也可以得到某些孤立的结论,比如C1 和C2,但是如果我们仅仅得到孤立的结论,我们是远远不能解决问题的.从命题者的角度来说,一道难题并不是简单的从A 到B 的逻辑推理,而是多种知识点的整合,也就是联系,才能让学生多角度调动知识点,全面考察学生能力.“联系”观点的建立,其重要性不言而喻.美国著名哲学家和教育理论家杜威认为,好的思维习惯的培养,取决受教育者的背景性格已经生活环境,同时也取决于施教者的引导.因此无论是前面三种具体的方法,还是“联系”观点的培养,都离不开这两个个条件.这也是培养好的思维方式的唯一途径.