培养解题反思习惯 提升数学解题能力

广东省东莞市东莞中学松山湖学校(523000)冯强泉

提升解题能力是数学教学的重要任务之一.现实教学中,往往注重让学生大量练习,期望通过题海战术快速培养学生的解题能力,但效果并不理想.著名数学教育家波利亚把解题过程分成四个步骤：(1)理解题目;(2)拟定方案;(3)实行方案;(4)回顾.[1]这说明,得出了数学题的答案,并不意味着解题思维活动的结束,而是深度思维的开始.但一直以来,教师很少引导学生反思,学生缺乏反思意识,不知怎么反思,这直接影响学生数学解题能力的发展.数学教师应加强引导学生进行解题反思,培养学生的反思习惯.提升解题能力.

一、精心设计解题教学,引导学生反思

解题反思,应该反思什么? 反思是指学习者对自身数学学习活动的过程及活动过程中涉及的有关事物(材料、信息、思维、结果等)学习特征的反向思考.[2]因此,在解题教学中,教师要课前精心设计,课中灵活变通,引导学生从结果、思路、方法、规律、推广等方面展开反思.

(一)反思解题结果

学生在解完一道题后,往往就心满意足,沾沾自喜,不再思考,这就错过了修正总结的的机会.教师要引导学生在一个数学解题结束后尽力去回忆自己从开始到结束的每一步心理活动,反思自己做的到底对不对? 还有没有条件没用上?还有没有其他答案? 哪里有疑问? 以后解题时应如何避免错误?

例1.1为美化环境,计划在某小区内用30 平方米的草皮铺设一块边长为10 米的等腰三角形绿地,请你求出这个等腰三角形绿地的另两边长.

评析学生容易想到需分类讨论,得出以下两种答案：设AB= 10 米,过点C作CD⊥AB,垂足为D,则即则CD=6 米.

① 如图1,当AB为底边时,AD=DB= 5 米,米;

②如图2,当AB为腰时,AB=AC= 10 米,AD=米,BD=2 米,米.

此时,教师要引导学生反思：还没有其他情况? 以上两种情况,都是髙在三角形的内部,是否有髙在三角形外部的情况? 学生想到第③种情况：

③ 如图3,当AB为腰且三角形是钝角三角形时,AB=BC= 10 米,米,AD=10+8=18 米,米.

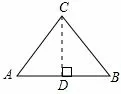
图1

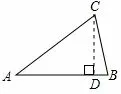
图2

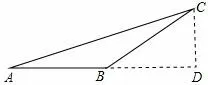
图3

教师在教学中需引导学生反思：解题是否需要分类讨论,分类讨论是否完整? 一般的,如果涉及到三角形的髙,需要分别考虑三角形的高在三角形内部和外部的情况.

例1.2如果关于x的一元二次方程(k+2)x2-3x+1=0 有实数根,那么k的取值范围是 ____.

评析此题显然考察一元二次方程的根的判别式,学生容易作出以下答案：

因为关于x的一元二次方程(k+2)x2-3x+1 = 0有实数根,所以Δ ≥0,即(-3)2-4(k+2)×1 ≥0,解得所以答案为：

但其实,本题中二次项系数为(k+ 2),还需要保证即所以本题的正确答案是且

因此,在解题中,教师要引导学生反思：题目是否有隐藏的“坑”? 是否有条件被忽视了? 既要掌控大局,也要注重细节.

(二)反思解题思路

绝大部分学生在解题过程中,总在不断尝试,不断修正,解题思路并不十分清晰.为提高解题质量和效率,教师要引导学生回顾和整理解题思路,概括解题思想,使解题过程清晰化、思维条理化、精确化和概括化.

例2方程的|x-1|+|x+2|=5 的解为____.

评析本题可以运用绝对值的代数意义,分类讨论,比较麻烦.如果结合数轴进行解题,则事半功倍.画出数轴,|x-1|表示数轴上x的对应点到1 的对应点的距离,|x+2|=|x-(-2)|表示数轴上x的对应点到-2 的对应点的距离.容易得到,在-2 和1 之间,不存在满足条件的解.在-2 的左边,当x=-3 时,在1 的右边,当x= 2 时,满足条件.故x=2,或者-3.得出答案后,教师要引导学生反思：本题的解题思路是什么? 让学生明确：本题通过数形结合,把代数问题转化为几何问题.

(三)反思解题方法

教师应该积极指导学生对解题方法进行自我总结和反思,帮助学生进一步深化对数学应用的认知,有利于学生综合解决和梳理出习题的多种思维和方法,帮助学生巩固基本的解题思路.[3]很多数学问题都有多种解法,寻找出多种解法,可以发开阔学生的解题思路,发展学生的思维能力.因此,教师要引导学生反思：还有其他方法吗? 哪种方法最优?

例3如图4,AB是半圆O的直径,点P在BA的延长线上,PD切⊙O于点C,BD⊥PD,垂足为D,连接BC.

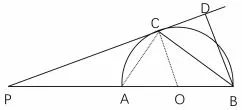
图4

(1)求证：BC平分∠PBD;

评析第(2)问,连接AC,可证得△PAC～△PCB,可得得解得PB=12.故OA=3.运用相似三角形的知识求出答案后,教师要引导学生反思：此题还有其他方法吗? 得到解法2：连接OC,则△OPC为直角三角形,设半径为r,则得解得r= 3.通过反思,让学生初步理解：圆背景下求线段的长度常用两种方法：①相似三角形方法 ②构造直角三角形方法.

(四)反思解题规律

数学问题形式多样,千变万化,但很多问题本质相同,解题有共同的规律,教师要引导学生反思,基于现有问题而衍生出形异而质同的问题,加深对问题本质的认识,[4]深入理解解题规律,解一题,通一类,切实掌握解题方法.

例4有n个人,每两个人握一次手,共有多少次握手?

评析因为每一个人都要与其他的人握手,故每一个人要握(n-1)次手,全部人共需握手n×(n-1)次.但每两个人之间只握了一次手,这种算法是重复计算了一遍,故实际上全部人共握手次.

在解决这个问题后,教师要引导学生反思：这个问题与之前学过的哪类问题相似? 从而帮助学生明白此类“握手问题”与“平面上有n个点,任意3 点都不在同一条线上,则这n个点可以连出几条直线”、“同一条直线上的n个点可以形成多少条线段”、“同一个顶点出发的n条射线可以形成几个角”、“n支球队两两赛一场共需赛几场”问题本质相同”、与“n个同学两两互送礼物共送多少礼物”思维相似,因而能深刻理解这一类问题的解决方法.

(五)反思问题推广

对数学问题进行推广,既能让学生进一步深入理解题目的解法,又能促使学生根据变化了的条件、问题进行积极思考,从而寻求解决问题的方法,培养学生的创造性思维.因此,教师应该引导学生反思问题本身,对问题进行推广.

例5如 图5,在Rt△ABC中,∠ACB= 90°,AC= 8,BC= 6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1 个单位长度,当点P运动到C时,两点都停止.设运动时间为t秒.

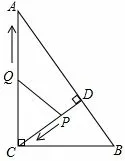
图5

(1)求线段CD的长;

(2)是否存在某一时刻t,使得QP⊥CD?

(3)设△CPQ的面积为S,求S与t之间的函数关系式.

评析教师要引导学生反思：你能根据第(2)问提出其他问题并给出解答吗? 有学生提出问题：是否存在某一时刻t,使得△CPQ是直角三角形? 此问需考虑另外两种可能存在的情况：①∠PQC= 90°②∠QCP= 90°.画出图形后运用相似三角形的对应边的比相等即可解决.还有学生提出问题：是否存在某一时刻t,使得△CPQ是等腰三角形? 此问让学生从直角三角形的视觉转到了等腰三角形的视觉,要考虑可能的三种情况：①CQ=CP②PQ=PC③QP=QC.画出图形,运用等腰三角形的性质、相似三角形的性质等知识即可解决.此举让学生开阔了视野,让学生从整体上把握问题,从更髙观点看待问题,通过一道题体验“动点与直角三角形”、“动点与等腰三角形”两类题的解题方略,提升解题能力.

二、合理实施各项举措,促进学生反思

反思含有自我质疑的成分,学生往往在内心容易产生抵触情绪,不愿意反思.所以单凭教师的的引导、示范,不足以形成反思的技能和反思的意识,教师必须实施各项举措,促进学生反思.

(一)向学生说明反思的重要性,激发内驱力

心理学研究表明,当学生知道了做一件事情的必要性,知道做了有什么作用,知道了怎么做,才会乐意去做.因此,教师应该通过讲道理,列举事例等方式,向学生说明反思的重要性,激发学生的内在动机,变“要我学”为“我要学”,促进反思的常态化.

(二)留出时间,让学生反思

传统的教学,课堂上要么老师满堂灌,要么布置很多题目给学生做,学生不能成为课堂的主人;课后,布置大量的解题作业,基本没有时间进行反思.反思需要时间,因此教师要注意留出时间,比如在课堂上解题后给出时间让学生专门进行反思,并给时间让学生交流反思所得,体验快乐.课后,布置少一些题目,留出时间让学生解题后进行反思.

(三)引导学生撰写反思记录

撰写反思记录,可以记录学生的反思过程,反思结果,让学生体验成就感,进一步提升反思的效果,同时,也是督促学生切实进行反思的有效措施,帮助学生逐渐养成解题反思习惯.为了鼓励学生撰写反思记录,教师应该评选优秀反思记录,进行表扬激励.

总之,教师应该多想办法,多利用各种机会,主动创造条件让学生学会解题反思,调动学生积极性,促进学生养成解题反思的习惯.让学生在反思中感悟学习数学的乐趣,在反思中感悟数学能力提升的成功体验,在数学反思中不断获得自身的成长!