生长型数学专题复习课教学探索——以“矩形折叠问题”为例

广东省中山市中山纪念中学(528454)汪晶晶

在历年的中考数学中,矩形折叠问题常常受到出题人的青睐,以广东省中考为例,近五年有四年考查(见表1).原因在于矩形是特殊的平行四边形,在初中数学教材中处于非常重要的地位,不仅是前面三角形知识的延续,而且是后续学习圆等其它知识的基础.此外,矩形折叠问题不仅包含丰富的知识点,而且蕴含重要的数学思想方法,是对学生知识、能力和思维的综合考查.以矩形折叠问题开展专题复习,能够促进学生基础知识、基本技能、基本思想、基本活动经验的发展,从而发展核心素养.

?

生长型数学专题复习是指围绕某个核心知识点(重点、难点、疑点)或某个问题(基本问题、基本图形、基本思想、基本方法),运用变式、拓展、延伸产生知识、方法、思维、经验生长链,形成核心知识间的结构关系,揭示出解决问题的规律和方法,领悟数学思想方法,积累数学活动经验,提升数学思维品质.生长型数学专题复习不只是数学知识内部再生长,内容重构重组,也是思想方法经验积累式生长、学生思维的递进式生长,更是思维品质、生命品质的生长[1].近期,笔者上了一节“矩形折叠问题”生长型数学专题复习课,希望各位同行批评指正.

一、“矩形折叠问题”课例分析

课前学生准备好一张矩形纸片,在课堂上动手折叠.

问题1如图1,有一张矩形纸片ABCD,AB= 6,AD=8,你能折叠出面积最大的正方形吗？

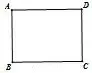
图1

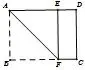
图2

如图2,学生折叠矩形纸片得出答案,教师进一步追问：(1)为什么四边形ABFE是正方形？(2)你能根据已知条件,求出哪些线段的长度？

分析此题改编自人教2013 版义务教育教科书八年级数学下册59页练习第1 题.作为基本问题,是本节课的“生长源”.此题的起点低,为后续的生长提供了空间.在教学中,学生都能够完成,不仅激发学生学习兴趣,而且充分尊重每一个生命个体.学生通过动手折叠,积累基本活动经验.教师通过追问,促进学生理解,使“生长源”不断向下扎根,加深“生长源”在学生头脑中的印象,形成解题模型,积累“生长源”.

问题2如图3,继续在剩下的矩形纸片按上述操作折叠,求A、H两点间的距离.

图3

教师进一步追问：以此操作继续下去,最终能得到几个正方形,边长分别是多少？

分析此题是2017年广东省中考的第16 题,不仅是“生长源”的变式,而且在问题1 的基础上生长.求两点间的距离,即是求两点间线段的长度,将此线段放在直角三角形中,利用勾股定理求得,促进学生求两点间距离方法的生长.继续操作下去,体现极限思想,促进学生思维的生长.

问题3如图4,在矩形纸片ABCD中,AB=6,BC=8,将纸片折叠,使得点B落在对角线AC上的E处,折痕为AF,求BF的长.

图4

问题4若AB= 6,点E恰好为AC中点,则BF=____.

问题5若AB=6,BC=3BF,则BF=____.

分析问题3,将原来的矩形纸片的宽折叠至对角线处,求BF 的长.此题需要设未知数,利用勾股定理列方程.问题5 是2016年广东省中考第15 题的改编,问题3 是在问题1的基础上生长,而问题4 和问题5 是在问题3 的基础上生长,使其特殊化.问题4 和问题5 均要用到“直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角是30°”这一重要知识点或者是锐角三角函数知识.因此,这三个问题串,在“生长源”的基础上,生长了知识链,同时方法链也得到生长.学生体会到方程思想,化归思想,以及一般到特殊思想,思维链也得到生长.学生积累了矩形折叠问题的解题经验,生长了经验链.

问题6如图5,先将矩形纸片ABCD沿三等分线折叠后得到折痕MN,再将纸片折叠,使得点B落在折痕MN上E处,折痕为AF,求BF的长.

图5

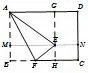
图6

分析问题6 是将宽折叠,使点B落在三等分线处.此题有一定的难度,利用之前的方法不能得以解决.需要过点E作AD边的垂线,构造两个直角三角形,利用R t△AGE～R t△EHF求得.因此,这个问题使学生的知识链、方法链都得到生长,学生的思维也进一步生长为高阶思维,再一次积累了解题经验,生长经验链.在此,学生跨越了一个生长“结点”,虽然经历了生长的痛苦,但更多的是体验到生长的快乐与欣喜.

问题7本节课研究思路怎样？引导学生从知识、方法、思想、经验等方面进行梳理归纳,然后教师用思维导图形式呈现小结.

分析从生长理念引导学生自主梳理、归纳本节课核心内容与方法,使知识、方法、经验、思维结构化、直观化,有利于促进学生认知结构化.

课后作业

1.(2015年广东中考第21 题改编)如图7,在折叠得到的边长为6 的正方形ABFE中,G是边EF的中点,将△AEG沿AG对折至△AGH,延长GH交边BF于点I,连接AI,则BI的长是( )

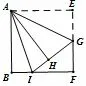
图7

A.1 B.2 C.3 D.4

2.如图8,在矩形纸片ABCD中,AB= 6,BC= 8,将纸片折叠,使得点C落在AD边上的F处,折痕为BE,则CE=____.

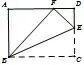
图8

3.(2018年广东中考第22 题改编)如图9,在矩形纸片ABCD中,AB= 6,BC= 8,把矩形沿对角线BD所在直线折叠,使点C落在点E处,AD交BE于点F,连接AF.

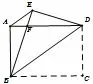
图9

(1)求证：△AEF是等腰三角形;

(2)求tan ∠BAF的值.

4.(2012年广东中考第21 题改编)在第3 题中,线段GH交AD于点K,把△GDH沿GH折叠,使点D落在A处,点D恰好与点A重合.求GH的长.

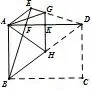
图10

分析巩固课堂知识和方法,进一步领悟数学思想,使知识、方法、思维和经验链得以继续生长.课后作业与课堂上的问题形成系统化,有利于学生认知结构整体化、系统化的形成.

二、生长型数学专题复习课的实践思考

(一)生长源是核心

生长源是专题复习课的核心.根据生长型数学专题复习课的内涵可知,生长源是某个核心知识点(重点、难点、疑点)或某个问题(基本问题、基本图形、基本思想、基本方法),整节课设计的问题都要围绕生长源变式、拓展和延伸,学生的知识链、方法链、思维链、经验链在生长源的基础上生长.生长源好比一粒种子,只有好的种子,才能发芽、枝繁叶茂,直至长成参天大树.从数学教学心理学的角度,学习的过程就是知识迁移的过程.当人们遇到一个新问题,往往想起一个过去已经解决的相似问题(源问题),并运用源问题的解决方法和程序去解决新问题,这一问题解决策略被称为类比迁移[2].因此,对于学生而言,在解决新问题时能够联想到一个过去已经解决的相似问题是知识迁移的关键.在生长型数学专题复习课中,生长源是学生在今后遇到相似问题时能够联想到的源问题,生长源的重要性不言而喻.

本节课中的问题1 是生长源,来源于课本基础练习题,起点较低.问题2 到问题6,以及课后作业,都围绕问题1 设计,学生的知识链、方法链、思维链、经验链在生长源的基础上生长.问题1 简洁,便于学生今后遇到矩形折叠问题类比迁移.生长源的选取要结合教材与中考题,可以是数学问题,也可以是几何图形,比如“8 字形”、“双平等腰型”、“一线三等角”等.

(二)生长性是目的

生长性是专题复习课的目的.所谓生长性,由生长源出发,基于基础与经验,在解决问题过程中不断产生新问题,不断生长新的数学知识、方法、思维、经验.任何一节数学课,都要有教学目的,所有的设计问题及活动都是为达到这个目的服务的.一节好的数学课,教学目的是发展学生的四基.数学专题复习课也不例外,对于复习课,教学目的不能简单停留在知识点的回忆和复习,应以发展学生四基为目的,重建知识结构,领悟重要思想方法,积累数学活动经验,提升思维品质,发展核心素养,学生的知识链、方法链、思维链和经验链都要生长.因此,在生长型数学专题复习课中,变式、拓展、延伸出问题链是方式,生长性是目的.

本节课由生长源变式、拓展、延伸生长的知识链、方法链、思维链和经验链如下图11：

图11

(三)层次性是前提

层次性是专题复习课的前提.教育的根本任务是立德树人,数学教师应成为学生发展的导师,教数学知识是手段,育人是目的,而育人的前提是尊重每个生命个体.教师设计问题基于每位学生的学情,为不同层次的学生制定恰当的教学目标,设计问题具有层次性就是尊重学生的表现.《义务教育数学课程标准(2011年版)》中课程基本理念为数学课程应致力于实现义务教育阶段的培养目标,要面向全体学生,适应学生个性发展的需要,使得：人人都能获得良好的数学教育,不同的人在数学上得到不同的发展[3].生长型专题复习课的情怀源于生命,立意基于生长,本质体现发展,价值就在于尊重生命,放飞思维,收获素养[4].因此,生长型数学专题复习课要关注每一位学生的发展,设计的问题要体现层次性,由易到难,从低阶思维到高阶思维.

本节课以生长源为出发点,起点低,面向全体学生,尊重每一个生命个体.问题串以生长源为核心,着眼于学生的最近发展区,由易到难变式,促进学生知识链、方法链、思维链、经验链的生长,超越其最近发展区而达到下一发展阶段的水平.

(四)结构化是关键

结构化是专题复习课的关键.复习课难,专题复习课更难,难就难在重建或完善学生认知结构.现代学习理论表明,数学学习的实质是学生在教师的引导下能动地建构数学认知结构,并使自己得到全面发展的过程.专题复习课的内容应具备结构化特点,是激活学生重建或完善认知结构的催化剂,为学生生长提供必备的养料.因此,结构化是专题复习课的关键,决定着发展学生认知结构的成败.生长型数学专题复习以整体观架构,形成以生长源为核心的认知结构,体现知识的整体性和结构性,有利于重建或完善学生认知结构.

本节课中课堂教学中的由七个问题组成的问题串和课后作业的设计体现了如图12 的结构性：

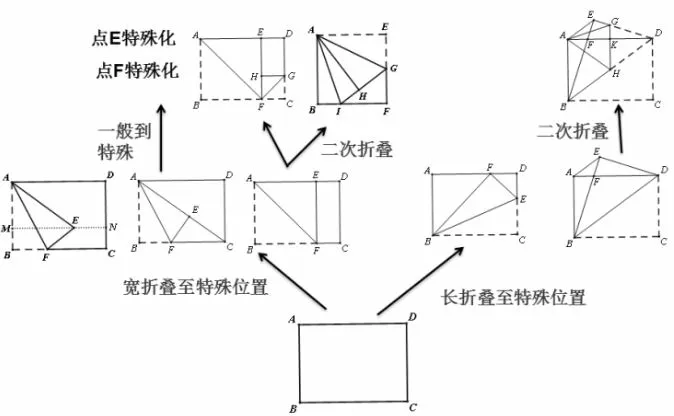
图12

生长型数学专题复习课最根本的出发点与落脚点都是每一个生命个体,在实际教学中,教师要基于学生学情,对于数学素养有待提高的班级,一定要“扎根”,不可“拔苗助长”,盲目生长.