专题复习助力数学核心素养“落地生根”——以“K”型全等基本图形专题复习教学设计为例

广东省深圳中学龙岗初级中学(518000)黄小华

“当今世界各国教育都在聚焦对于人的核心素养的培养”,[1]我国也不例外,核心素养已成为我国教育界普遍关注的一大焦点.如何在课堂教学中落实数学核心素养,这是一线数学教师共同关心的话题,章建跃先生指出,教好数学就是落实数学核心素养,而教好数学的前提是理解数学,[2]笔者以“K”型全等基本图形专题复习教学设计为例,展示“K”型全等的设计理解,探讨如何预设更加符合数学核心素养的教学设计.

一、案例设计

1 基本图形,构建模型

问题1如图1,等腰三角形△ABC中,∠ACB= 90°,CA=CB,直线ED经过点C,过点A作AD⊥DE于点D,过点B作BE⊥DE于点E,求证：△ADC～=△CEB.

图1

设计追问

(1)为什么叫“K”型全等基本图形,你能找出图1中的“K”吗?

(2)适当变换图形位置,如图2,这四个图形与图1有什么区别和联系?“K”型全等基本图形必须具备哪几个条件,其中最重要的结论是什么.

图2

设计意图从学生熟悉的情景入手,唤醒学生对已有知识的回忆,两个追问有利于学生自己建立起“K”型全等基本图形; 通过图形变式,学生能充分理解“K”型全等基本图形的本质.

2 模型应用,思维生成

2.1 简单应用

问题2 如图3,在平面直角坐标 系中,∠ACB= 90°,CA=CB,过点B作BE⊥OE于点E,若OA=4,OC=3,求点B的坐标.

图3

设计意图将“K”型全等基本图形放入平面直角坐标系中,代数与几何有机结合,为后面基本图形综合应用做好铺垫.

2.2 图形变换

问题3如图4,直线与x轴和y轴分别交于A,C两点,将直线AC绕着点A逆时针旋转45°得到直线l,求直线l的解析式.

图4

设计追问

(1)求直线l的解析式,根据待定系数法,还缺什么条件,

(2)结合问题2,你有什么启发.

设计意图旋转、平移、对称等图形运动是几何变换中的基本形式,这里要求学生构造“K”型全等基本图形,能很好促进学生思维活动,有利于学生思维体操运动.

2.3 综合应用

问题4如图5,直线与x轴和y轴分别交于A,C两点,在第一象限内找个点M,使△ACM是等腰直角三角形,试求点M的坐标.

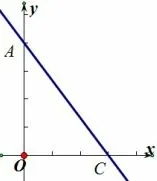
图5

设计追问

(1)从直观想象角度,你觉得有几个点符合题意,用三角板画画看.

(2)结合问题3,你尝试采用分类讨论的思想逐步把符合题意的几个点求出来.

设计意图在问题3 的基础上延伸,有利于培养学生思维的连贯性和拓展性.

问题5 如图6,直线与x轴和y轴分别交于A,C两点,点P的坐标为P(2,3),试问直线上是否存在两点G、H,(点G在点H上方)使△PGH是等腰直角三角形,若存在,试求出点G的坐标,若不存在,试说明理由.

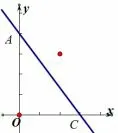
图6

设计追问

(1)请利用手中的等腰直角三角板在图6中画一画可能存在的等腰直角三角形,

(2)在你所画的等腰直角三角形中画出“K”型全等基本图形,

(3)在求点G的坐标中你有什么困难,请小组讨论并尝试着解决问题,

(4)在构造基本图形时应注意什么.

设计意图(1)如图7,学生动手画出等腰三角形,有利于培养学生的几何直观,

(2)如图8,学生在图7的基础上动手画出“K”型全等基本图形,学生能很好地领悟在平面直角坐标系构造“K”型全等基本图形的核心是向坐标轴作垂线或平行线补成一个“K”型全等基本图形,

(3)求点G的坐标确实有一定困难,小组讨论有利于学生用“字母”表示数的思想方法将动态转化静态,然后用方程思想加以解决问题.

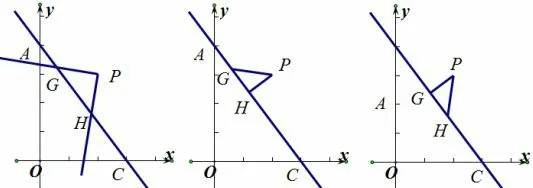
图7

图8

二、案例理解

“K”型全等基本图形是很重要的基本图形,也是全国各地中考试卷中常考常新的重要知识,为后面专题复习“K”型相似基本图形提供了类比的思路和方法,“K”型全等基本图形经常“潜伏”在不同的背景(如一次函数、反比函数、抛物线、圆等)中,只有理解其本质,学生才能运用自如,达到“万变不离其宗”的效果.

1 熟悉模型入手,突显人文关怀

“K”型全等基本图形是学生较熟悉的图形,初中数学各个版本的教材中都有相应的教材例题或习题,学生备感亲切,专题复习设计“K”型全等基本图形为后面“K”型相似基本图形及“一线三等角”做好准备,教学设计以基本图形为主旋律在结论上做不同深度的变式,绝大部分学生在不同程度上都能获得“跳一跳就能摘到苹果”的成就感,充分体现数学新课程标准中的“不同的人在数学上得到不同的发展”的理念.

2 问题层层递进,彰显思维过程

波利亚曾经说过“解题的成功,要靠正确的转化”.案例设计以基本图形为主线,按照“证明基本图形结论——理解基本图形本质——应用基本图形性质——做辅助线构建基本图形”模式组织学生进行有序的思维训练,学生在经历图形的分解、提炼、构造过程中提高自己的几何直观思维能力,同时案例设计还将图形和平面直角坐标系及函数问题相关联,为学生搭建了一个更广阔的思维平台,任学生“驰骋风云”,学生在“平台”上学会了思考,也学会了学习,充分促进和发展了学生的主体性[3].

3 追问触及本质,凸显数学素养

针对课堂提问存在急于求成、不求质量、设计随性等情况,案例设计强调高质量的追问,这些追问本身就渗透了转化思想,学生亲身经历从特殊到一般、从代数到方程、从代数到几何、从静态到动态深层次“半自学”历程,学生在习得数学知识的同时也习得了数学思想方法,真正促进了学生深度学习.

问题1 的追问有利于培养学生的几何直观,问题3 的追问有利于培养学生的构造和数学建模,问题4 的追问有利于培养学生的直观想象和分类讨论等逻辑推理,问题5 的追问有利于培养学生以动化静的思想,提升学生用方程解决几何问题的数学运算能力,这些不都是我们所提倡的核心素养吗.

三、案例思考

《普通高中数学课程标准(2017)》指出数学核心素养包含：数学抽象、数学建模、逻辑推理、数学运算、数据分析、直观想象六个方面[4],数学核心素养六个方面不是简单的相加,更不能将其看成这六部分的和[5],与《义务教育数学课程标准(2011)》十大核心概念相比不是概念异化,强调整体性和系统性,教学实践中如何践行数学核心素养? 我们一线教师不能割裂这些年来以《义务教育数学课程标准(2011)》为指导的数学教育,应在取得已有成果的基础上科学性系统性地做好每堂课的教学预设,让数学核心素养在课堂教学中“落地生根”.

数学核心素养“落地生根”的主阵地是课堂,教师只有先做好教学设计,才可能有精彩的课堂,数学核心素养“落地生根”的主体是学生,教学设计只有从学生出发,才可能“事半功倍”,我们教师的教学设计在“知识与技能”方面做得很好,但在“过程与方法”方面还大有作为,下面以案例设计为例谈谈自己在“过程与方法”方面对教学设计的一点看法.

1 促进学生深度学习

针对课堂教学教师包办过多、学生依赖较大等现象,案例设计以五个问题串为背景,学生自身经历了“数学意识、问题解决、逻辑推理、信息交流”[6]一系列由静到动、由浅入深、螺旋上升的变化过程,教师只是作为组织者创造了以学生为主体的课堂生态,通过五个问题串中的“追问”赋予学生更多的选择权,案例设计时刻意留给学生充分的时间和空间来掌握自己的学习,充分发挥了学生的主体性,学生处于“深自由呼吸、深思维运动”状态下的深度学习,培养了学生今后丢掉“拐杖”也会走路的良好思维品质.

教师在预设教学设计时要把握教材的整体性,孤立每一节课来谈数学核心素养是毫无意义的,专题复习也不例外,本案例设计的下一个教学设计为“K”型相似基本图形专题复习以及“一线三等角”基本图形,目的是把散乱但有关联的知识“串联”起来,使之形成一个系统,这样更加符合学生的认知规律,有利于培育学生深度学习的土壤,激发学生的探究欲望,让学生感受到数学的魅力.

2 丰富学生活动经验

我国古典数学中的“赵爽弦图”、“韩信点兵”、“杨辉三角”等一些重要的结论都得益于经验的积累,对数学发展产生了深远的影响,数学发展史本身就是一部经验传承史.

数学教师如何在教学设计上体现“丰富学生活动经验”这一理念? 案例设计在这个方面也做了一点尝试：学生动手操作构建基本图形,学生潜移默化地经历了观察、猜想、归纳、验证的数学活动经验;问题串呈现后学生独立思考,存在困惑时教师采用追问的方式,目的是让数学活动经验凸显,学生沿着主线不断探究从而积累数学活动经验;对于案例设计中的动态问题,教师采用小组合作交流的形式开展活动,学生在互帮互助中不断丰富自己的数学活动经验;学生通过构造基本图形的应用,数学活动经验在重构中“落地生根”;问题(5)追问“在构造基本图形时应注意什么”,目的是注意学生的反思,从而内化和升华学生的数学活动经验.

3 挖掘素材思想方法

案例以“证明基本图形结论——理解基本图形本质——应用基本图形性质——做辅助线转构建基本图形”为主线本身就是一种方法,这种方法对学生数学学习和教师高效预设教学设计提供了一种借鉴.

教师在做教学预设时,如何挖掘素材(教材、教参、学生习题、考试试卷、专题复习)的思想方法,这需要技巧和艺术,案例设计中做了一些巧妙的处理：案例设计中有意识渗透数学思想方法,如问题2 中的构造思想和数形结合思想,问题3中的化归思想,问题4 中的分类讨论思想和类比思想,问题5中的字母表示数的思想和方程思想等,这些思想方法在题中深藏不漏,但能统领解题的思路;案例设计中的追问另一个目的是引导学生运用数学思想方法进行分析,从而逐步培养学生运用数学思想方法的习惯;案例设计中的反思也是培养学生在解题后有意识归纳和提炼数学思想方法,进而不断反思和巩固数学思想方法.

数学核心素养的培育绝不是一朝一夕的事,作为数学核心素养“落地生根”的抓手――教师,只要心系数学核心素养,努力做好课堂预设,学生数学核心素养一定能“生根发芽”.