基于范希尔理论下的几何学习路径——以“三角形的认识及其内角和”教学设计为例

四川师范大学(610066)孙佳 张红

一、引言

平面几何是初中数学内容的重要主题之一,但从学生的掌握情况来看不容乐观.学生缺乏直观想象、逻辑推理等几何学习的素养,发展学生几何推理能力显得尤为重要[1].而现今课堂教学模式形式多样,教学材料丰富.导致一线教师在选择合适的教学方式出现困难,不能进行深度教学.作为几何教与学的基本理论框架,范希尔理论自诞生起,一直是备受关注的研究课题.笔者将基于范希尔几何思维理论,以“三角形的认识及其内角和”这一主题为例探讨如何进行教学设计.

二、范希尔几何思维理论

国内外学者对学生几何思维进行了许多研究,其中平面几何是中学数学的重要主题之一,而从一线教师反馈知学生的掌握情况不容乐观,其缺乏直观想象、逻辑推理等几何学习的素养.而范希尔几何思维水平理论既可以作为诊断学生几何思维水平的评估指标,也可以用于设计每个水平上的教学目标与任务[2].荷兰一线教学的教师范希尔夫妇关注了皮亚杰的工作,经过一段时间的研究,他们提出了几何思维的五个水平,如下[3]：

水平0：视觉,只能注意直观形状的某一些特征,根据直观上的形状相同来确认图形的分类;

水平1：分析,分析图形组成要素以及特征,并以此建立图形的特性,利用这些特性解决一些简单几何问题等;

水平2：非形式化的演绎;能够建立图形及图形性质之间的关系,可以提出非形式化的推论等;

水平3：形式的演绎,了解到证明的重要性,和了解“不定义元素”“公理”和“定理”的意义等;

水平4：严密性,能够在不同的公理体系下严谨地建立定义,以分析比较不同的几何系统等.

课标指出,几何图形的学习需要经历直观感知、操作确认、推理论证、度量计算四个过程.正如在对事物的认识过程中,也需要经历特殊到一般,由具体到抽象的过程.范希尔理论的四个水平恰好与之对应,并且目标更明确.

三、学生掌握三角形及其内角和所需的层次及教学设计

对于学习平面几何的第一个基本图形——三角形而言,学生对其的认识也需要经历：

水平0：三角形的初步认识——直观感知

这一个阶段属于“视觉”水平,即直观感知水平,学生能够感受到现实世界中确实存在三角形模型,而且这些图形之间具有关联性.

设计1观看视频,欣赏各种美丽图案,展示出示生活中的图片,如：风筝、自行车车架、红领巾、金字塔……学生看到图形所具有的共同特点[4].

设计2让学生画出展示图片的数学图形,通过将非本质属性去掉,留下“数学意义”下的图形.

图1 形式各异的三角形

学生潜意识感受到：三角形是一个三条线段围成的图形,还有三个角,有些边相等有些不等.

设计说明学生通过视觉直观感知,能够模仿画出三角形,使用自己的语言描述三角形的特点,考虑到学生的思维特点,设计1 的目的是通过展示直观图像,吸引学生的注意力.背景材料来自于生活情境,感受数学来源于生活.设计2通过去非本质属性,抓本质特点,感知三角形这一抽象图形的本质.

水平1：三角形的再认识

这一阶段属于“分析”水平,此阶段学生知道三角形的组成要素,并能够观察边与边的连接关系,角的大小关系,可以模仿着画出三角形,使用较为标准但不完全的语言描述三角形的概念.

(一)判断下列图形是三角形吗?[5]你能总结出三角形具有的特点吗? 能给三角形下定义吗?

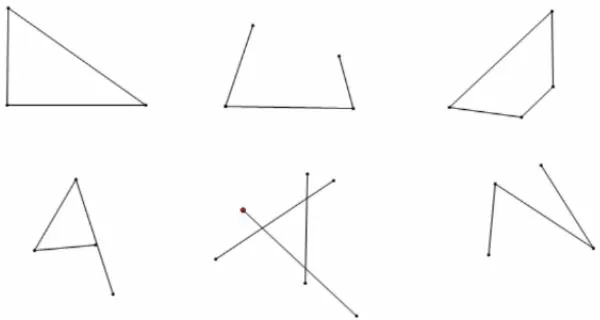
图2 三条线段组成的图形

(二)猜角游戏之“量一量”活动

教师提供不同样式的三角形,学生进行度量,并将角度标示在相应位置.请每小组代表说出自己度量的其中两个角的度数,教师猜测剩下角的度数.通过每组学生自己切身操作,发现教师给出的结果都在一个值左右波动,并大胆猜测三角形内角和是180°.其中引导学生讨论：为什么有的同学度量后计算的内角和不是180°呢?[6]进而进入下一环节.

水平2：三角形内角和的非形式化的验证——推理论证

这一阶段属于“非形式化演绎”水平,学生能够借助前述三角形之间的联系进入初级阶段的抽象思维水平,这一阶段初步揭示三角形的本质特点.

设计验证猜想之“剪一剪,拼一拼”活动.

课前让学生准备好不同类型的三角形：直角三角形、锐角三角形、钝角三角形纸片若干.课上以小组为单位,进行“剪一剪,拼一拼”活动.

说明：教材上运用折叠的方法证明三角形内角和是180°,是否还有其他的方法? 一种即可剪下其中两角,与第三个角拼在一起,发现是一个平角,即为180°.一种即用三个全等的三角形,将不同角拼在一起也会得到三角形内角和为180°.学生自己尝试操作,通过剪、拼等活动,能够深刻认识到图形之间的相关关系,并且能够为自己的猜想“三角形的内角和是180°”给一个合理的解释,从心理上获得成功的体验.

水平3：用数学推理的方式来证明三角形内角和为180°——推理论证

直观感知、操作确认下的教学活动只停留在数学的表面,数学定理一定是可以证明的,所以上述学生只处于“形式推理”水平.不过也只有在经历了这个过程,学生才能进行下一层次的学习.

设计学生进行的量一量,折一折、拼一拼等操作,得出三角形内角和是180°的规律,但是,这并不是数学,验证过程并非是数学意义的证明,下面引导学生运用平行线知识进行证明：

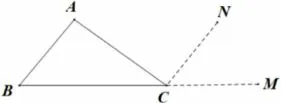
图3 作三角形一条边的平行线

证明延长BC到M,过点C作CN//AB,因为CN//AB,所以∠A= ∠ACN(两直线平行,内错角相等),∠B= ∠NCM(两直线平行,同位角相等).因为∠ACN+ ∠NCM+ ∠ACB= 180°(平 角180°),所 以∠A+∠B+∠ACB=180°(等量代换),即∠A+∠B+∠C=180°.

设计说明引申数学证明的方法,体现数学的严谨性,唤起学生对数学思想方法的回忆,从而找到知识的生长点以及获取知识的途径,同时激发学生探索的兴趣.

水平4：三角形的深层次理解——度量计算

在经历了直观感知、操作确认、推理论证后,要对三角形有更深入的认识,就必须对其进行数量刻画,即“度量计算”.

设计根据三角形内角和是180°的规律,如果知道三角形中两个内角的度数30°和70°,不用度量,你能计算出第3个角的度数吗?

变式1在直角三角形,已知其中角为60°,求另外一个角?

变式2如图,已知∠BAC=90°,AD⊥BC,垂足是D.

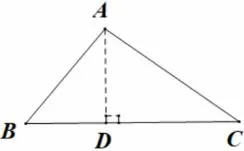
图4 作三角形的一条高

(1)计算∠B+∠C,图中有几个是直角三角形,是哪几个? 分别说出他们的直角边和斜边?

(2)∠BAD和∠B有什么关系? ∠CAD和∠C呢?

设计说明由于三角形内角和的重点在于内角和的推演过程以及内角和为180°这一定理.因此,例题的选取较为基础,主要为加深对定理的理解,通过适当的变式练习,深化对三角形的认识.

四、小结

平面几何是初中数学内容的重要主题之一,而从一线教师反馈知学生掌握情况不容乐观.学生缺乏直观想象、逻辑推理等几何学习能力,而由于学习任务繁杂,大多只是了解概念和记住公式,忽略了其中蕴含的数学思想方法,不能做到深度学习.以及现今课堂教学模式形式多样,教学材料丰富.导致一线教师在选择合适的教学方式出现困难,不能进行深度教学.仍有教师以讲授课本上的知识为主,导致学生处于一种机械性的学习当中,课堂气氛也比较沉闷.基于此,以“三角形及其内角和”这一主题为例,印证了几何学习需要经历直观感知,操作确认,推理论证,度量计算四个学习路径,领会几何学习的本质,教师通过进行深度教学,学生才能达到深度学习.