立足通性通法 寻求解题策略
——含参函数单调性分类讨论的标准
安徽省枞阳县会宫中学 (246740) 方明生
近几年的全国卷,导数均以压轴题的身份出现,难度教大,学生的得分普遍较低,让不少学生望而生畏.不管是求极值、最值、不等式证明还是函数零点的个数问题,最终都会涉及到含参函数的单调性,而正是这个参数“吓退”了我们的学生.追起根源,我们会发现含参函数的单调性问题的本质其实就是解含参的一元一次不等式、一元二次型不等式.而含参不等式的解法亦是高中不等式题型的难点,大部分学生根本把握不好分类讨论的标准,容易出现重复或者遗漏.通过笔者多年的教学,对此类题型形成了一点自己的见解,今天写出来供大家参考,不当之处请方家指正.
一、一元一次不等式型
例1 设函数f(x)=xekx,求f(x)的单调区间.
解:由题意可得f′(x)=ekx+kxekx=ekx(1+kx),易知ekx>0恒成立.


评注:原题求导后转化为求解不等式g(x)>0和g(x)<0,因为在解不等式过程中要将参数k除到右边,根据不等式的性质,此时就需要对k的正负进行讨论.故一元一次不等式讨论的标准是:(1)对一次项前的系数分正、负和零进行分类讨论;(2)在系数为正(或负)的情况下判断根是否在定义域内,从而进一步展开讨论.
二、一元二次不等式型

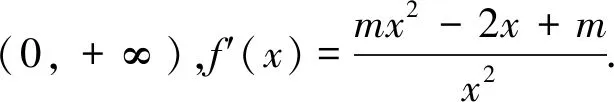
(1)当m=0时,f′(x)=-2x<0恒成立,所以f(x)在(0,+∞)上单调递减.
(2)当m>0时,函数g(x)开口朝上,Δ=4-4m2(对判别式正负进行讨论).
(ⅰ)当Δ≤0时,即m≥1,此时f′(x)≥0恒成立,故函数f(x)在(0,+∞)单调递增.


(3)当m<0时,(此步易判断f′(x)<0恒成立,考虑有部分学生做题时不善于去发现规律,故而笔者依旧按照对应的解题步骤去完成)函数g(x)开口朝下,Δ=4-4m2.
(ⅰ)当Δ≤0时,即m≤-1,此时f′(x)≤0恒成立,故函数f(x)在(0,+∞)单调递减.



评注:本题求导后进行通分,分母恒为正,故而不需要考虑分母的正负.解一元二次不等式关键在于二项式系数的正负讨论(学生容易忽略为零的情况)、根的存在以及根的大小.例2的讨论标准是对系数的正负以及判别式进行的讨论.
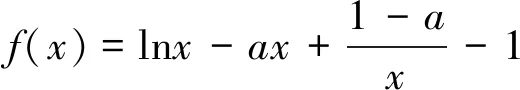
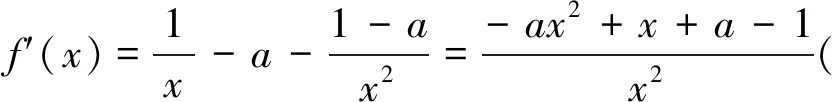
令g(x)=-ax2+x+a-1.
(1)当a=0时,g(x)=x-1(一次函数).令g(x)>0得到x>1;令g(x)<0,得0 (2)当a>0时,二次函数g(x)=-ax2+x+a-1的开口朝下,Δ=1+4a(a-1)=(2a-1)2≥0,所以g(x)=-(x-1)[ax+(a-1)](对判别式正负展开讨论) 评注:本题讨论较为繁琐,与例2的不同地方在于本题的分子可以直接因式分解,也是高考常考题型,对于能够因式分解的题型,直接进入第三步,先判断根是否在定义域内,再对两根大小展开讨论即可,无需再考虑判别式的正负.如果不按照分类讨论的标准进行极易出现错误. 通过上面的几个典型例题我们发现,对于求导后是一元一次不等式型,分类讨论标准为:第一步若一次项系数含参,需要对一次项系数的正负展开讨论;第二步求出对应方程的根后判断根是否在定义域内展开讨论. 求导后为一元二次不等式型,分类讨论的标准为: 第一步:看二次项系数是否含参,若含参,需要对系数分大于零、等于零和小于零分别展开讨论.若二次项系数为零,按照一元一次不等式题型解决;当二次项系数大于零(或小于零)进入第二步; 第二步:求出对应一元二次方程的判别式,分Δ≤0(函数在定义域上恒增或恒减)和Δ>0展开讨论.若Δ>0则进入第三步; 第三步:当Δ>0时,求出对应方程的两个不等实根. ①判断两个实根是否在定义域内,如果不能直接判断,需要展开讨论.其中两个实根都不在定义域内或者只有一个实根在定义域内可直接解二次不等式(或借助二次函数图像).若两个实根都在定义域内,则需要进入下一步. ②判断两根大小关系,若无法确定大小,则需要对两根的大小展开讨论. 最后,提供几道试题供参考: 1.(2019年长沙市第五次调研文科第21题节选)已知函数f(x)=lnx+ax2,其中a∈R,讨论函数f(x)的单调性. 3.(2017年天津文科数学第21题节选)已知函数f(x)=x3-6x2-3a(a-4)x+b,其中a,b∈R,|a|<1,讨论函数f(x)的单调性. 4.(2016年四川高考文科数学第21题节选)设函数f(x)=ax2-a-lnx,其中a∈R,讨论函数f(x)的单调性.

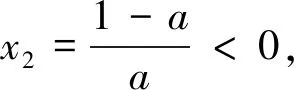
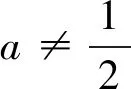
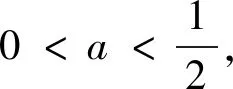



三、总结反思