圆锥曲线切线的一个定点伴随定直线的性质
2019-10-14 02:06安徽省合肥市第一中学230601偰永锋
中学数学研究(江西) 2019年9期
安徽省合肥市第一中学 (230601) 偰永锋
圆锥曲线作为高中数学里非常重要的一个内容,有很多优美的性质.很多圆锥曲线试题,往往背后都蕴含着圆锥曲线一般性质.高考也往往从这些性质出发设计出优质的试题,这就要求我们不仅要教会学生解题,还要加强对问题背后原理的探究.
笔者在高三一轮复习教学圆锥曲线时,遇到一个蕴含了美妙的圆锥曲线切线性质的题目.

图1
题目如图1,已知抛物线C:y2=2px(p>0)的焦点为F,准线为l,过l上一点P作抛物线C的两条切线,切点分别为A、B,若|PA|=3,
|PB|=4,则|PF|=.
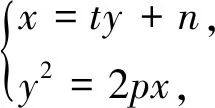
记A(x1,y1),B(x2,y2),则y1+y2=2pt,y1y2=-2pn.又切线PA:y1y=p(x1+x),PB:y2y=p(x2+x).
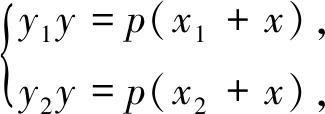

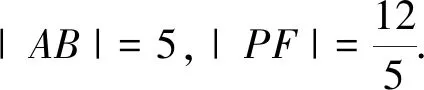
通过上述解题过程显然可以得到抛物线的切线有如下的性质:
性质1 过抛物线y2=2px的准线l上任意一点P作抛物线的切线PA、PB,切点分别为A、B,则切点弦AB恒过焦点F,且有PA⊥PB,PF⊥AB.
上述结论的逆命题也成立.
性质2 过抛物线y2=2px的任意一条焦点弦AB的两个端点分别作抛物线的切线PA、PB,则两条切线的交点P在准线上,且有PA⊥PB,PF⊥AB.
这两条性质可以作出进一步推广.通过探究发现:改变弦AB所过定点M的位置,两条切线PA与PB不一定垂直,但它们的交点P还在定直线上.PM与AB也不一定垂直,但当AB斜率存在时,kPM·kAB为定值.


证明过程与上述问题解决过程类似,此处从略.
这个性质在椭圆和双曲线中还成立吗?经过探究发现仍然成立.于是,在椭圆中有




类似地,在双曲线中有
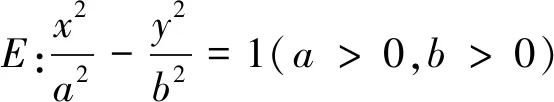
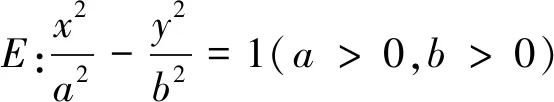

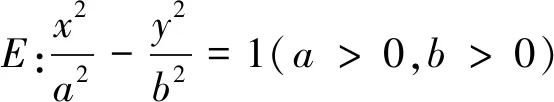
椭圆和双曲线中的性质及推广证明过程类似,下面证明推广3,其余从略.

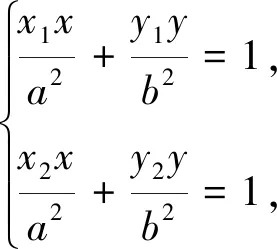
猜你喜欢
中学数学研究(江西)(2022年5期)2022-05-08
中学数学研究(江西)(2021年8期)2021-09-06
中学生数理化(高中版.高考数学)(2020年12期)2021-01-13
中等数学(2018年7期)2018-11-10
中学生数理化·教与学(2017年1期)2017-01-19
福建中学数学(2016年7期)2016-12-03
福建中学数学(2016年4期)2016-10-19
福建中学数学(2013年1期)2013-03-06
数理化学习·高一二版(2009年2期)2009-03-30
中学数学研究(2008年3期)2008-12-09

