基于核心素养下概念课教学的思考——以弧度制教学设计为例

浙江省安吉县孝丰高级中学 (313301) 夏吉伟

随着新课改的不断深化，数学核心素养越来越引起数学界广泛关注.但是，很多中学阶段的教师对数学核心素养的概念还不是很清楚，在教学中缺乏在数学核心素养视角下设计教学，一定程度上影响了学生数学核心素养的培养.那么，在课堂中如何在数学核心素养视角下设计教学，提升学生的数学核心素养的呢？

本文以弧度制教学设计为例，谈谈在高中数学概念课教学中如何提升学生的核心素养.

一、回顾旧知 类比引入

教学片断一

师：上一节课，我们把角的概念推广到了任意角，包括正角、负角、零角.这节课，我们进一步学习任意角的度量，回忆一下，初中学过哪些度量角的单位？

生1：度、分、秒.

师：那你能说说10是如何定义的吗？度、分、秒又如何换算呢？

师：这种以度、分、秒为单位度量角的制度称为角度制.

师：我们知道，各种度量制一般不是唯一的，比如长度、重量，既有国际公制，又有中国市制.那么，量角的度制是否只有角度制一种呢？是否有可能有、又有需要有另一种度量角的度制呢？

点评：在学生已有角的度量制——角度制的概念的基础上通过类比长度、重量等单位引入，提出问题，鼓励学生大胆猜想，激发学生的学习兴趣，唤起学生探究新知的欲望，培养学生的逻辑推理、直观想象等数学核心素养．

二、感知抽象 形成概念

教学片断二

师：当我们把一个平角记为“1π”时，那么360°、180°、90°、60°分别对应多少π呢？

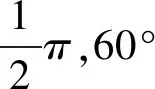
师：这就意味着角的另外一种度量是可能的，我们知道半径为r的圆周角的弧长为2πr，那么大小为n°的圆心角所对的弧长是多少呢？

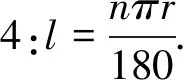
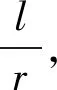
师：刚才是圆心角=90°，半径r=1,2,3,4的情况，接下来我们用几何画板来观察一下当圆心角和半径改变时，这个结论是否成立.

用几何画板演示:

生众：这个结论依然成立.

(师生共同讨论)归纳：

点评：上面从理性地角度，采用了特殊到一般，具体到抽象地思维过程验证了可以采用弧长与半径的比值来度量角的大小，通过直观感知、归纳推理和抽象概括等思维活动，提升学生的逻辑推理、直观想象、数学抽象等核心素养.

三、运用概念 加深理解

教学片断三

师：在半径为r的圆中，弧长等于2r的圆心角的弧度数是多少?弧长等于3r的圆心角呢?长度为l的弧所对的圆心角的弧度数又是多少?通过计算你发现什么圆心角与弧长和半径有什么关系呢？由此引导学生共同探讨.

师：很好！值得表扬.那么我们利用这个结论来算算当圆心角为-2rad时，它的弧长为多少？

生6：我算出弧长为-2r.

师：弧长能为负吗？问题出在哪呢？

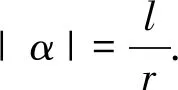
师：非常好！那我们一起归纳如下：

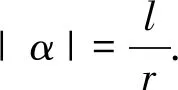
2.正角的弧度数是一个正数，负角的弧度数是一个负数，零角的弧度数是零.这样就在角的集合与实数集之间建立了一一对应关系.

设计意图：通过本环节使学生明白通过旋转，弧度制度量角的大小可以和实数集建立一一对应的关系，培养学生数学抽象、逻辑推理等数学核心素养.

四、学习互化 揭示联系

教学片断四

师：由上面的探究我们可以知道用角度制与弧度制度量同一角的大小，以角度与弧度度量平角可以得到180°=π弧度，由此出发，1°等于多少弧度？1rad等于多少度？

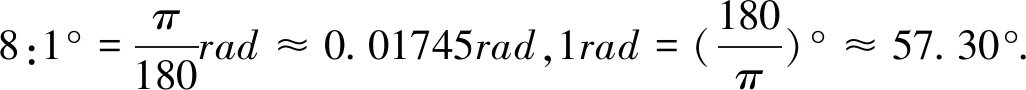
师：利用以上转化完成以下例题.

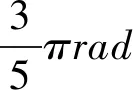
学生思考、板书，教师小结.

设计意图：进一步让学生明白角度制与弧度制可以度量同一个角，所以它们之间可以互换并要掌握这种互换，同时要注意规范及掌握一些特殊角的角度和弧度值.培养学生数学运算、逻辑推理等数学核心素养.

五、反思总结 提升高度

数学概念是反映现实世界的空间形式和数量关系本质属性的思维形式,它是是构成数学知识大厦的基石，是进行逻辑思维的第一要素，是数学思想和方法的载体，是数学教学的核心与基础，也是解决数学问题的前提.因此，在概念教学中，必须注重概念的形成过程，引导学生主动地亲身经历概念的形成过程，追求自然生成的概念教学，真正掌握数学概念.笔者觉得概念课教学要注意以下三个环节：

环节一 概念的生成：概念课教学不能照本宣科，教学中要注重揭示数学概念形成的过程，激发学生学习数学的兴趣，引导学生经历概念的发现和生成过程，让学生在感性认识的基础上，经过数学建构，形成数学概念，并理解数学概念.

环节二 概念的抽象：数学概念是培养学生核心素养、提升学生数学思维能力的一个重要载体，是基础知识中的基础，是学生对后续知识理解的基础.学生对概念的认识是一个从具体到抽象、从特殊到一般的过程.因而在教学过程中，我们不但要让学生经历概念形成的过程，更要注重概念的定性把握、定量刻画、抽象概括、准确表达，进而形成精确的数学概念.

环节三 概念的运用：概念教学中，老师要引导学生运用概念去解决数学问题，通过实例来说明概念，加深对概念的理解，培养学生的思维能力，提升学生的数学素养.只有当学生将所学的数学概念运用于生活实际，数学概念才能得以巩固，数学思维才能得以提升，数学能力才能得以提高.

总之，我们在平时教学中要核心素养的指导下，注重概念的生成、抽象和运用，不能把概念习题化，从此做到真正的培养学生的核心素养.