小课堂大素养——以“多参数函数问题”习题课为例

江西省萍乡市湘东中学 (337016) 彭小奇

一、问题的提出

进入高三复习后,习题讲评课成为常态课型.很多教师为了赶进度追求课堂容量,满堂灌地把答案讲完,至于思路如何形成,学生能否想到,这些题的解决需要学生具备什么知识储备,要形成哪些核心素养却思之甚少.甚至有部分教师认为提升核心素养是高一高二讲授新课才应该考虑的问题.

本文以多参数函数问题的习题课为例来阐述提升核心素养如何在高三课堂中落地生根.不当之处，敬请指正.

二、课堂实录

师：通过思考请哪位同学来说说思路？

师：很好,通过引入参数t能反解出b,a,进而达到消参的目的,最后只剩一个变量t,转化为我们的常规问题了.请同学们动手解出答案,待会投影展示同学们的规范解答.

(展示规范解答后)

师：还有没有其它方法可行？(没同学回答)那请同学们思考下面的变式.

变式1y=a分别与y=2x+2和y=x+lnx交于A,B两点,则AB最小值=．

师：这个变式和刚才所讲例题是同一类型吗？还能继续引进变量再消元的方法吗？请同学们试一试.

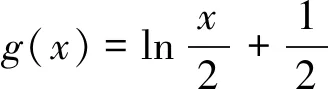
师：几位同学非常不错,生3没有思维固化去反解,而是直接用x2表示x1达到整体消元的目的.生2和生4两位同学利用图形直观帮助解题,非常好.希望同学们从多个角度去思考问题.

例2 已知f(x)=2lnx-ax2+3,∃m,n∈[1,5]，当n-m≥2时,有f(m)=f(n),则a的最大值为( ).

师：本题由平行x轴的直线与两函数图像相交变为一直线与一个函数图像相交,两交点的距离不小于2,反过来求参数的最值.请同学们认真思考.

师：方法很好,答案也对.先由f(x)极值初步确定a的范围,通过区间长度确定m,n的范围,要有f(m)=f(n),只需f(m+2)=f(m)有解,进而利用图形直观帮助解题.其他同学还有什么好的想法吗？

师：生6在最后求a时参变分离进行优化,两个函数之积的单调性判断其前提都要为正,大题还是求导判断更好.

生7：按生5的思路,1≤m≤3≤n≤5,只需f(3)≥f(m)≥f(1),f(3)≥f(n)≥f(5),解不等式即可.

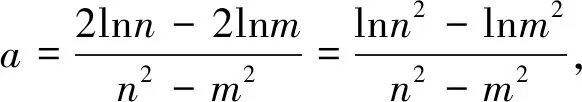
例3 已知a,b∈R,ex≥a(x-1)+b恒成立,则ab的最大值为( ).

师：本题结构非常简洁,几何意义也明显,请同学们看看能不能解决？

师：生9从不等式结构出发分析得到ab的最大值不能确定,转而构造函数求得其最小值f(lna)≥b,达到消去参数b的目的.很不错,分析到位！本题是2012年全国卷21题核心部分的改编.

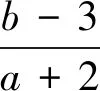
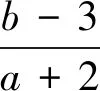
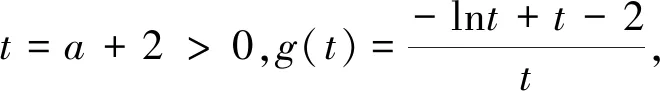
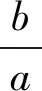
这时一男生迫不及待站起来想发言.

师：生11不拘泥于减元思路,利用图形直观解决本题.非常棒！今天的讨论非常热烈,同学们不仅仅满足于把题解出来,从不同角度去分析,给出了非常好的解法,老师也收获颇多.希望同学们保持这种精神,多思多想！即将下课,请同学们课后继续研究下面的变式.

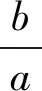
三、教学反思

《普通高中数学课程标准(2017年版)》指出：数学核心素养是数学课程目标的集中体现,是具有数学基本特征的思维品质、关键能力以及情感、态度与价值观的综合体现,是在数学学习和应用的过程中逐步形成和发展的.数学学科核心素养包括：数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析.这些数学学科核心素养既相对独立、又相互交融,是一个有机的整体[1].本堂课所选习题表象都是多参数问题,但所用方法各有千秋,有各种方式减元消参,也有保留参数利用图形直观整体解决的.学生的观察点不同,其切入点也就不同,所形成的不同核心素养也必将相互交融.

有些教师的搞题型分类课,反复训练,希望学生能形成条件反射,见到什么题型就用什么套路,僵化学生思维.对于数学核心素养的教学,史宁中教授认为应该从以下几个方面进行：把握数学知识的本质,把握学生认知的过程;创设合适的教学情境,提出合适的数学问题;启发学生思考,鼓励学生与教师交流、学生之间相互交流；让学生在思考和交流中、在掌握知识与技能的同时,理解知识的本质;感悟数学思想,积累思维的经验,形成和发展数学核心素养[2].

讲好数学习题课需要教师深入理解数学核心素养,遵循学生认知规律设计合理的问题串,调动学生积极性,引导学生多角度探讨,最终全方位提升数学核心素养.